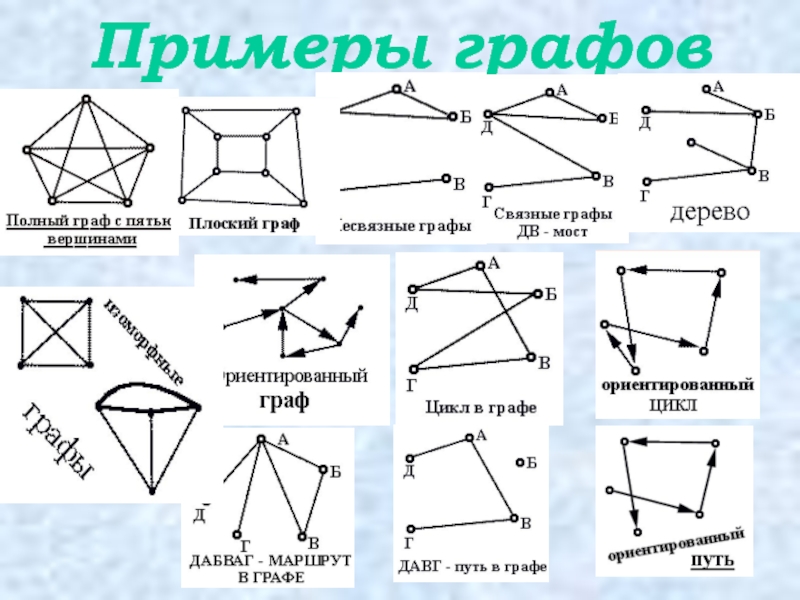
Взвешенные графы: ключевые особенности и методы работы с ними
Взвешенные графы — это структуры данных, где ребра имеют значения, представляющие их вес. Такие графы широко применяются в задачах, связанных с оптимизацией, маршрутизацией и анализом сетевых структур. Важными аспектами работы с ними являются поиск кратчайшего пути, минимизация затрат и анализ связи между объектами. В данной статье собраны полезные советы и методы, которые помогут лучше понять и эффективно использовать взвешенные графы.
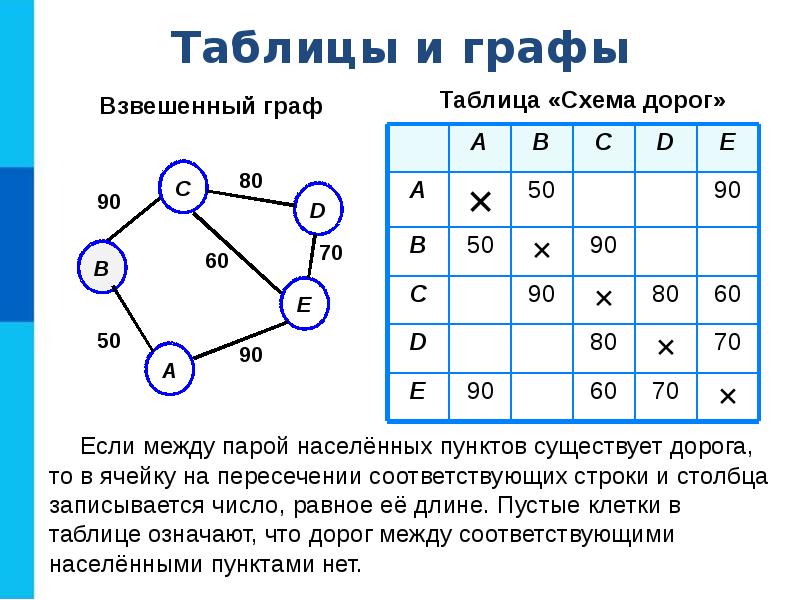
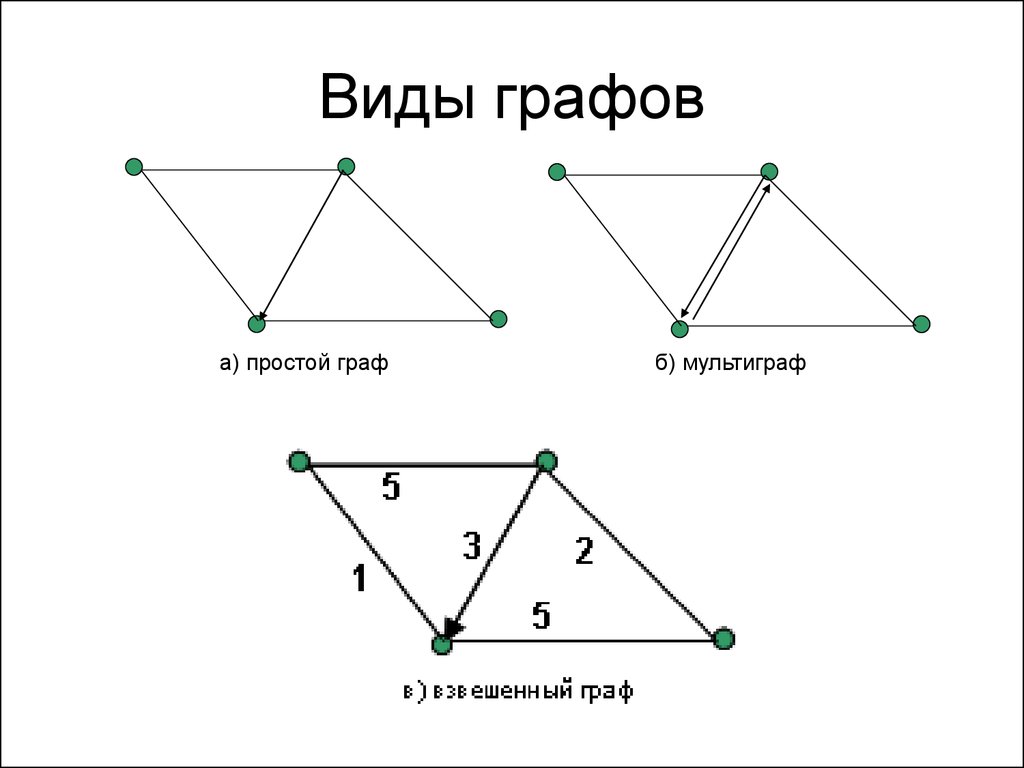
Перед тем как работать с взвешенным графом, важно четко определить, что именно представляет собой вес ребра — расстояние, стоимость, время или другое значение.
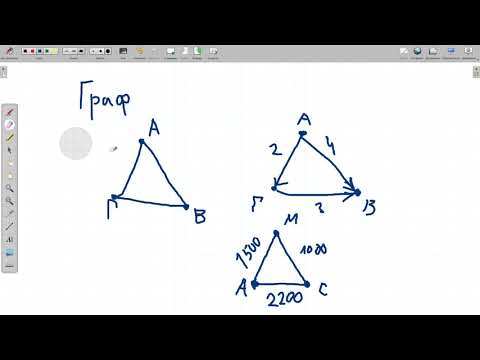
Информатика 9 класс. Взвешенный граф. Задание 6 страница 30.
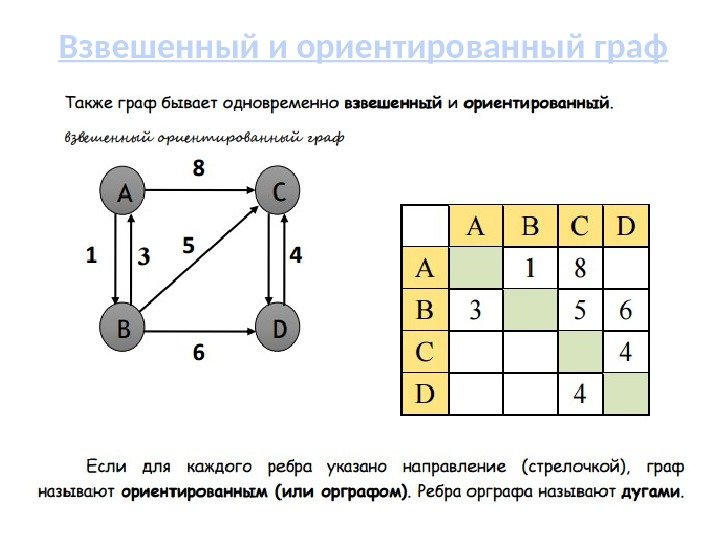
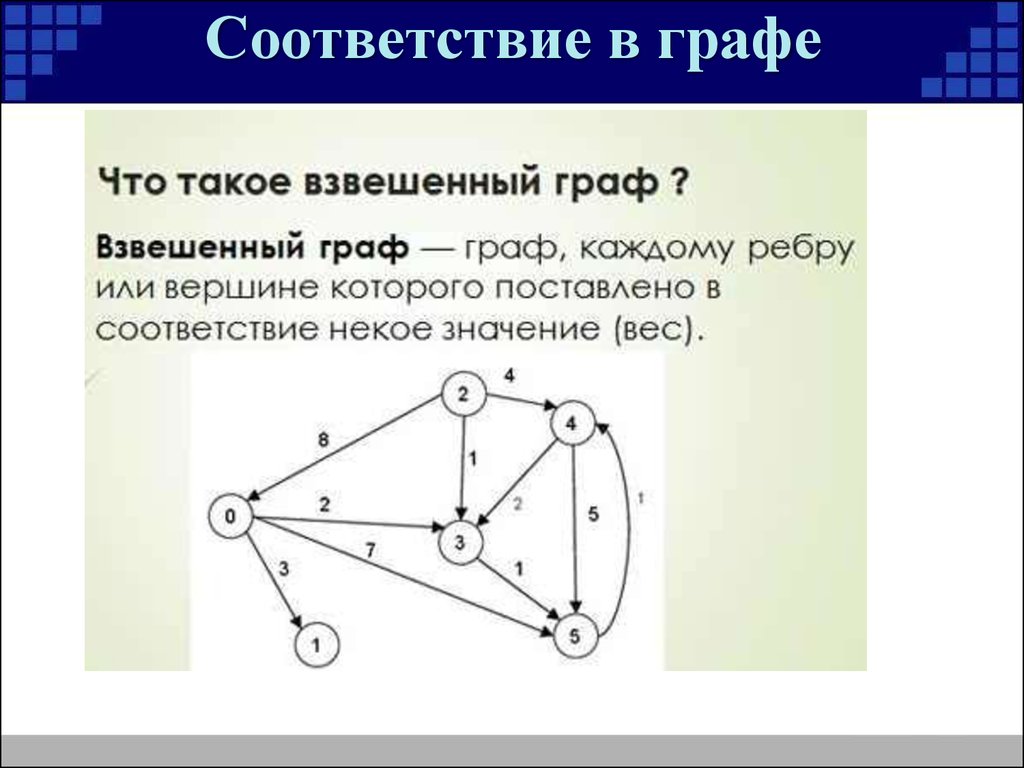
При использовании алгоритмов поиска кратчайшего пути, таких как алгоритм Дейкстры, убедитесь, что все веса ребер неотрицательные, так как алгоритм не работает с отрицательными значениями.

КАК РАБОТАЮТ ГРАФЫ - СТРУКТУРЫ ДАННЫХ
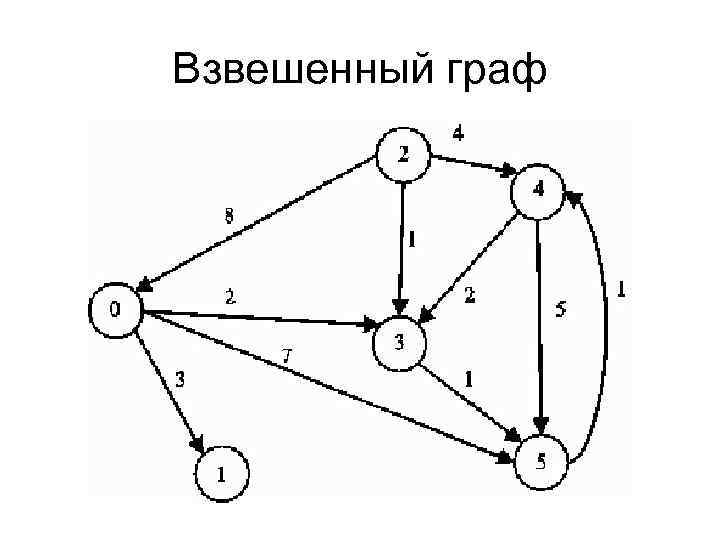
Для более сложных задач, например, поиска минимального остовного дерева, используйте алгоритм Прима или Краскала, которые эффективно работают с взвешенными графами.

№ 151 - Информатика 6 класс Босова (взвешенный граф)
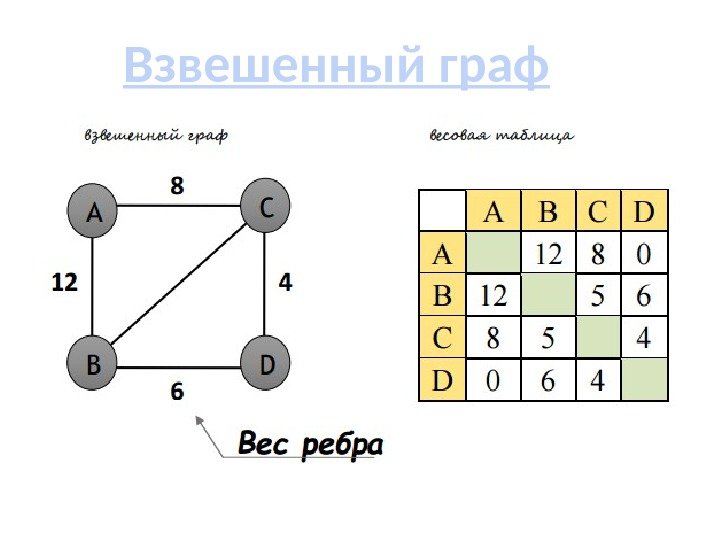
Если необходимо работать с большими графами, используйте структуры данных, такие как кучи, для эффективной реализации алгоритмов поиска и обновления кратчайших путей.

Информатика Типы графов

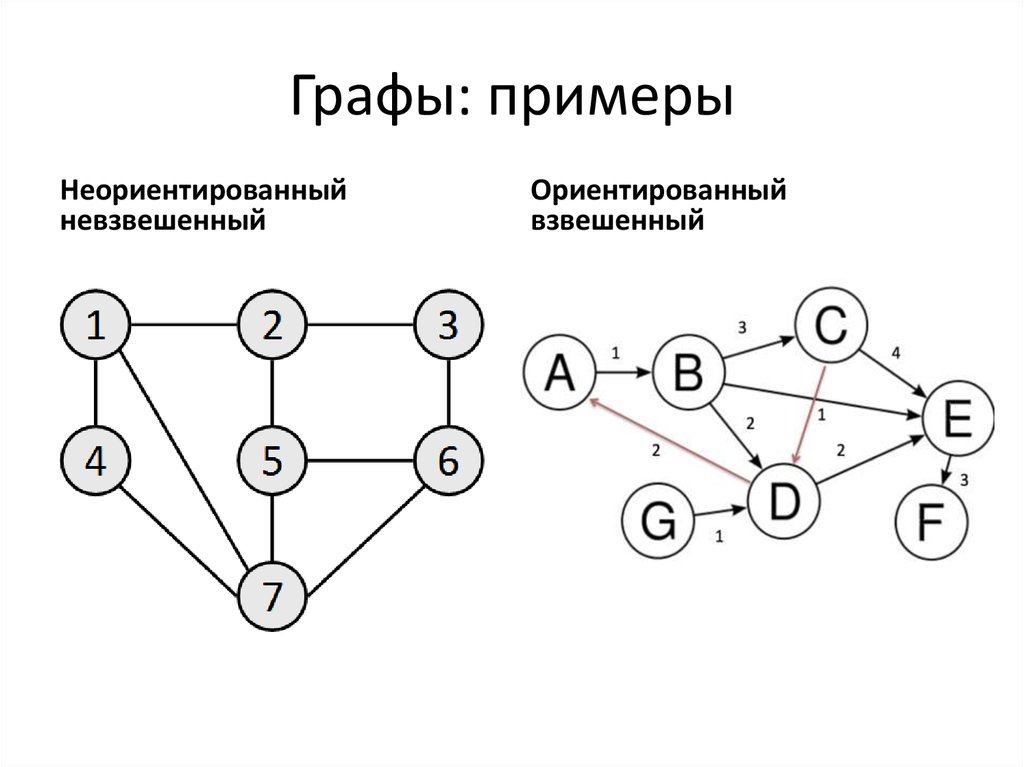
Обратите внимание на плотность графа: для разреженных графов могут подойти специализированные алгоритмы, которые значительно сокращают вычислительные затраты.
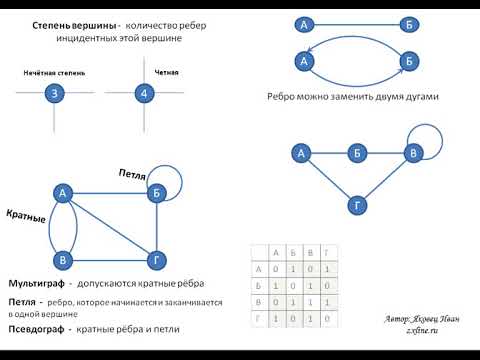
Графы, вершины, ребра, инцидентность, смежность
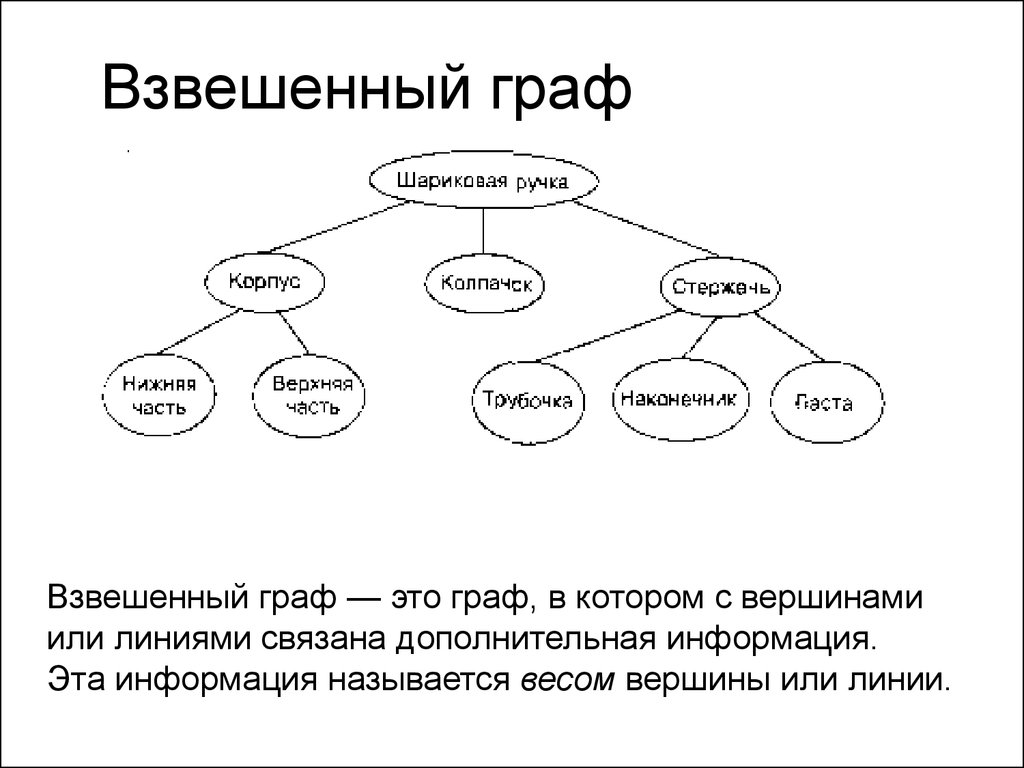
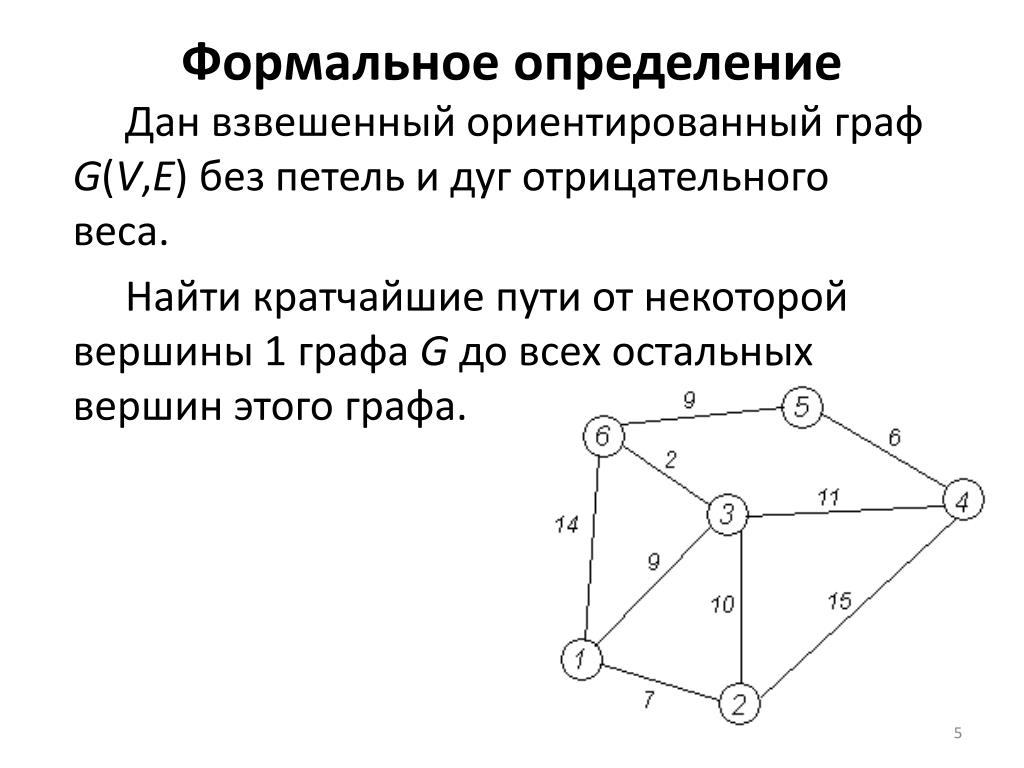
В случаях, когда веса ребер могут изменяться динамически, рассмотрите использование адаптивных алгоритмов, таких как алгоритм Флойда-Уоршелла, который эффективно решает задачи с изменяющимися весами.

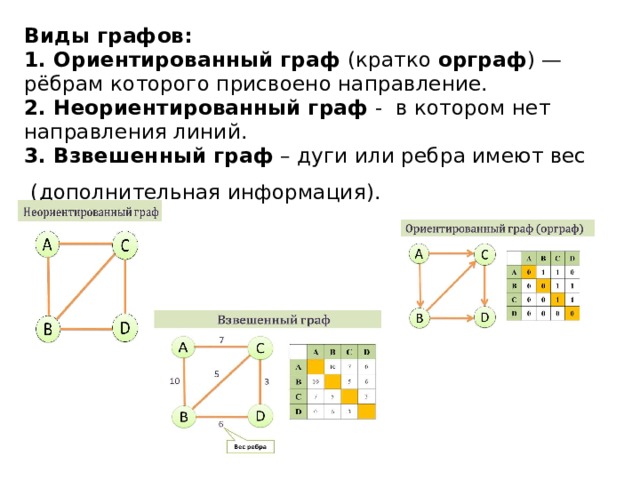
ЕГЭ - Задание 3 - Видео 2: Матрица смежности взвешенного графа
При построении графов для анализа сетевых структур учтите, что взвешенные графы могут помочь в более точном моделировании реальных процессов, таких как потоки данных или нагрузки на сети.
Для решения задач с отрицательными весами ребер используйте алгоритм Беллмана-Форда, который позволяет находить кратчайшие пути в графах с такими условиями.

Использование матриц смежности или списков смежности — это важный момент при реализации взвешенных графов, так как выбор структуры данных влияет на производительность алгоритмов.

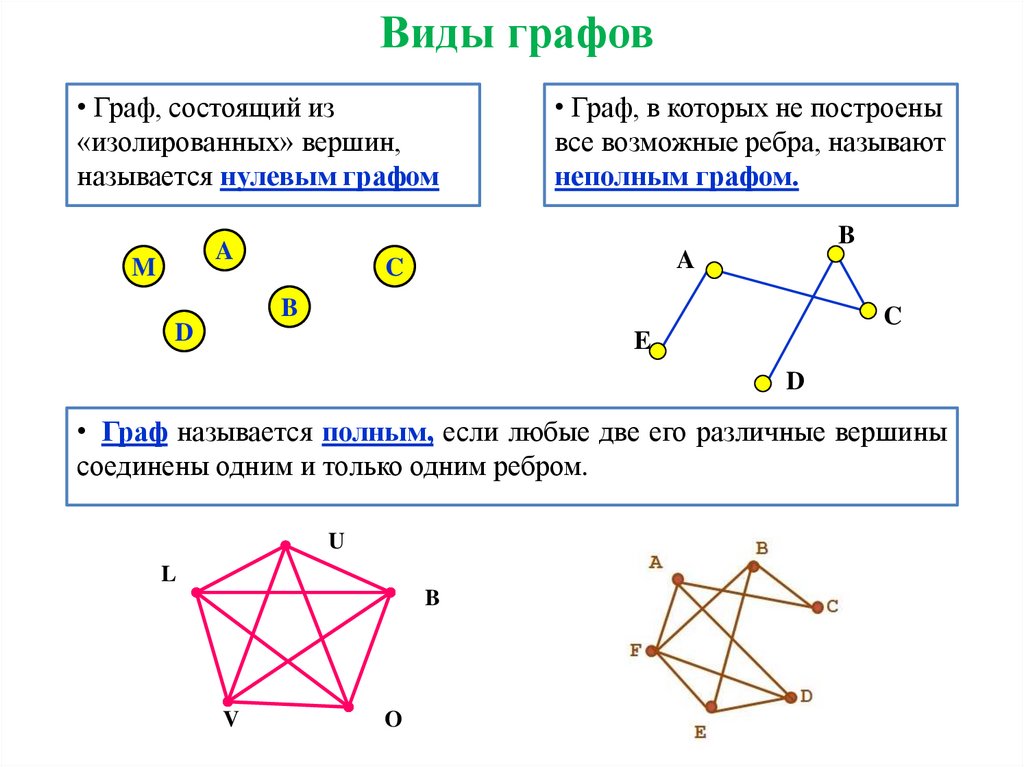
4.1 Виды и способы задания графов
Не забывайте проверять граф на наличие циклов с отрицательным весом, так как такие циклы могут привести к ошибочным результатам при поиске кратчайшего пути.