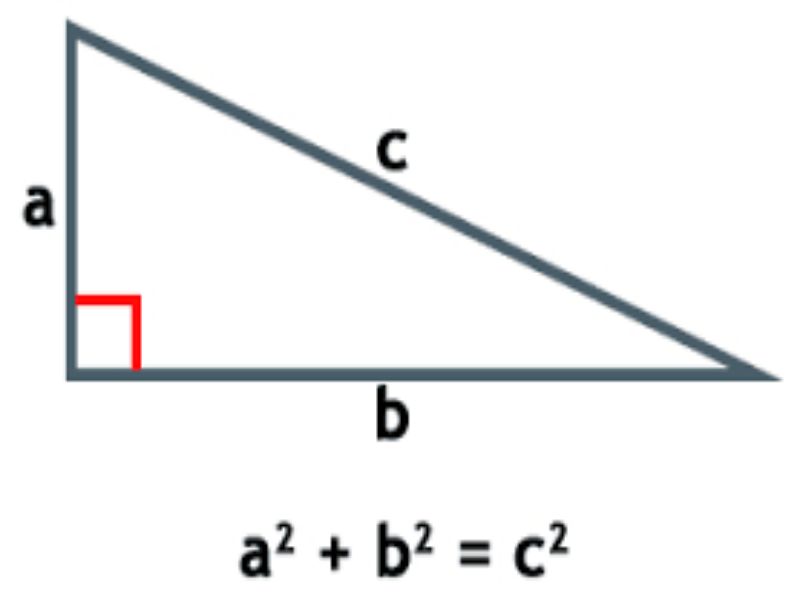
Применение теоремы Пифагора для нахождения длины хорды окружности
На этой странице вы найдете полезные советы и фотографии, которые помогут понять, как теорема Пифагора используется для вычисления длины хорды в различных геометрических задачах. Мы подробно объясним, как с помощью известных формул легко найти нужные значения и применить их на практике.


Чтобы вычислить длину хорды, используйте теорему Пифагора для прямоугольного треугольника, образующегося при проведении радиуса к середине хорды.

Как разделить круг на равные части

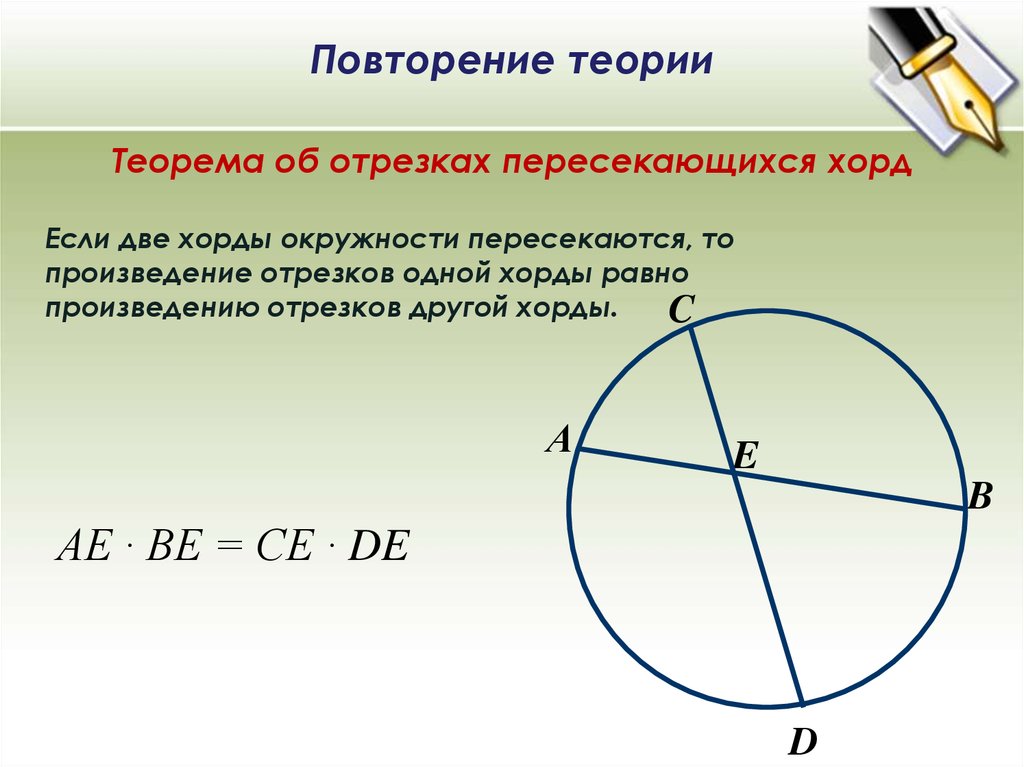
Важно помнить, что длина хорды зависит от расстояния от центра окружности до хорды и радиуса окружности.

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте Сегмента

При использовании теоремы Пифагора для хорды, обязательно проверяйте правильность вычислений, особенно если задачи связаны с кругами и углами.

Применение теоремы Пифагора в строительстве


Если вам нужно найти длину хорды, можно начать с вычисления половины хорды, используя радиус и перпендикуляр, проведенный из центра окружности.

Теорема Пифагора. 8 КЛАСС - Математика - TutorOnline
Помните, что теорема Пифагора применяется только в прямоугольных треугольниках, поэтому для вычислений следует всегда убеждаться в корректности построений.

уроки Пифагора аудиокнига

Для нахождения длины хорды, иногда удобно использовать формулы, в которых напрямую учитывается радиус окружности и расстояние от центра до хорды.

Прогульщик опоздал на 20-мин. и получил две ЗАДАЧИ... Его ответ поставил профессора в ступор...
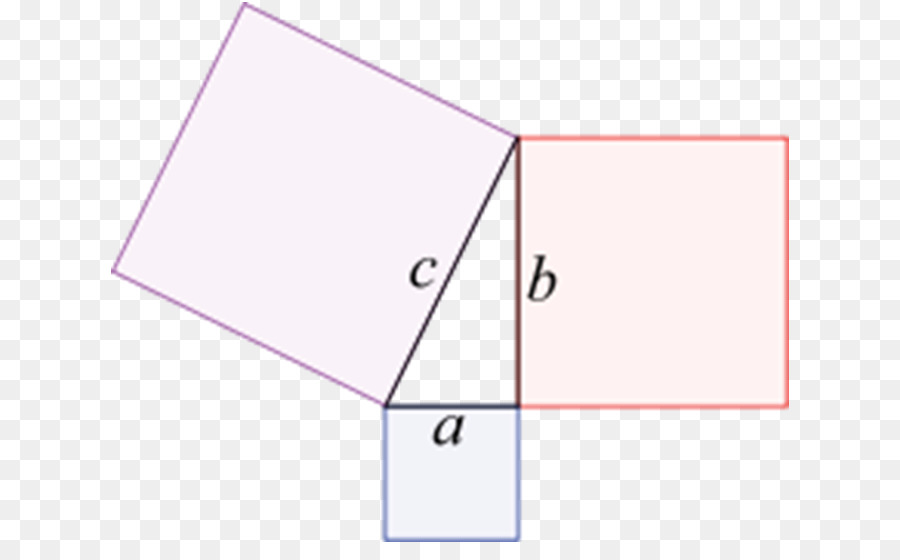
В некоторых задачах, чтобы получить точный результат, можно использовать графические методы и построения с применением теоремы Пифагора.

Окружность. Длина хорды. Теорема синусов.
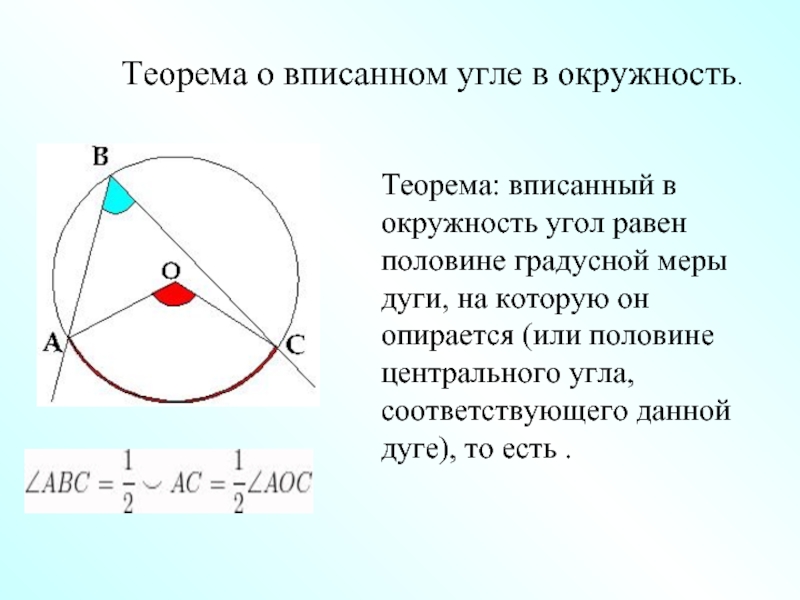
Если в задаче даны углы, можно также использовать теорему синусов или косинусов в сочетании с теоремой Пифагора для точных расчетов длины хорды.

Edu: Сколькими способами можно доказать теорему Пифагора?
Не забывайте, что правильное визуальное представление задачи и построение всех элементов фигуры поможет упростить решение задачи.
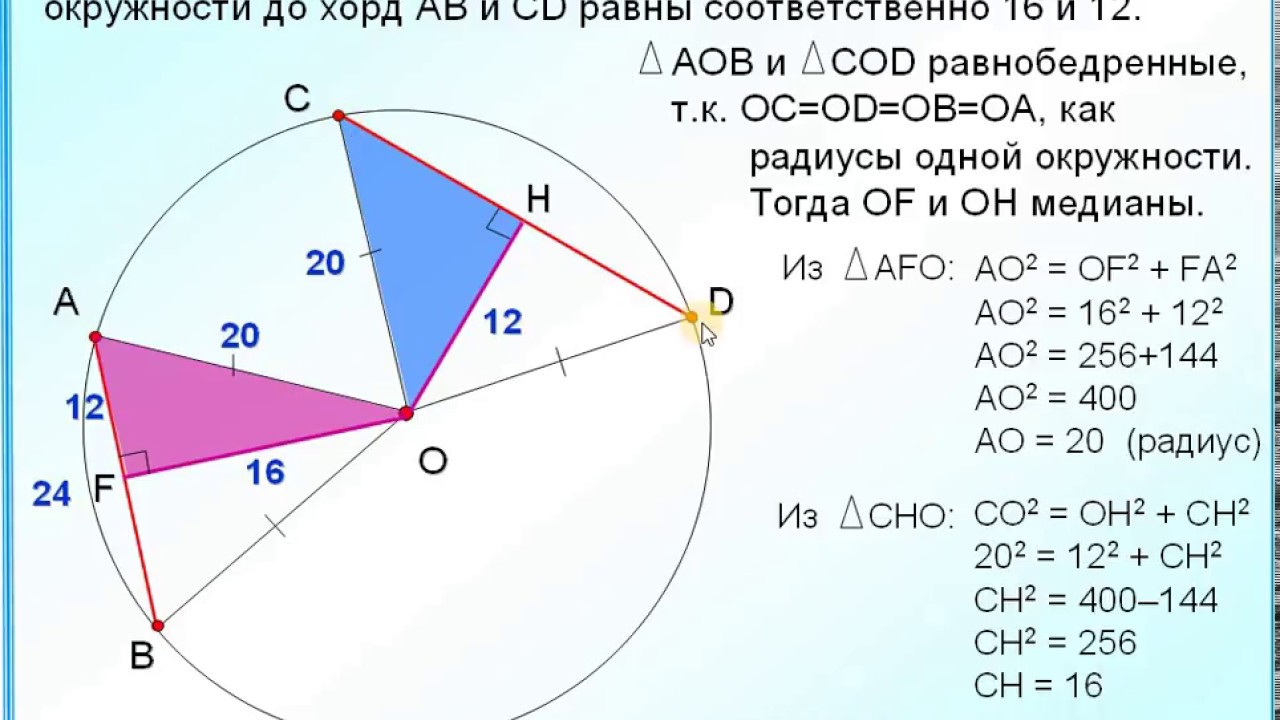

Для более сложных задач, включающих несколько окружностей или множества хорды, можно использовать системы уравнений, сочетая их с теоремой Пифагора для нахождения точных значений.