Понимание теоремы о биссектрисе треугольника для школьников 8 класса
Теорема о биссектрисе треугольника является важной частью геометрии для учащихся 8 класса. Она помогает лучше понять свойства углов и сторон треугольников, а также развивает логическое мышление. В этом разделе собраны полезные советы и визуальные материалы для более легкого усвоения теоремы и ее применения на практике.
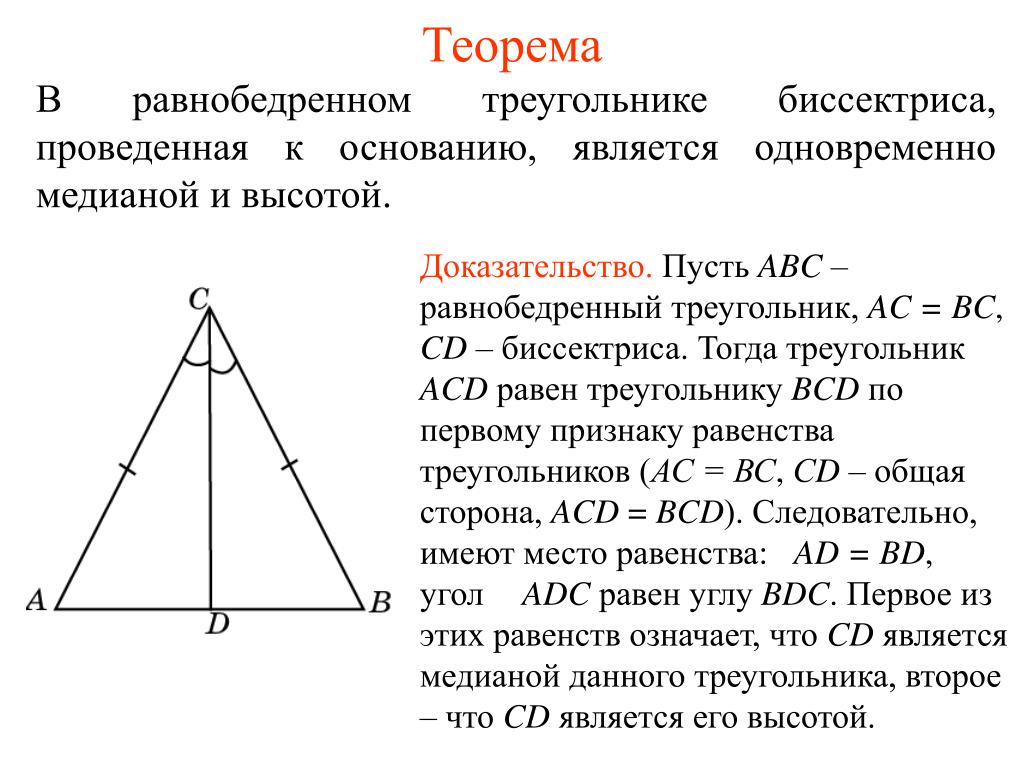
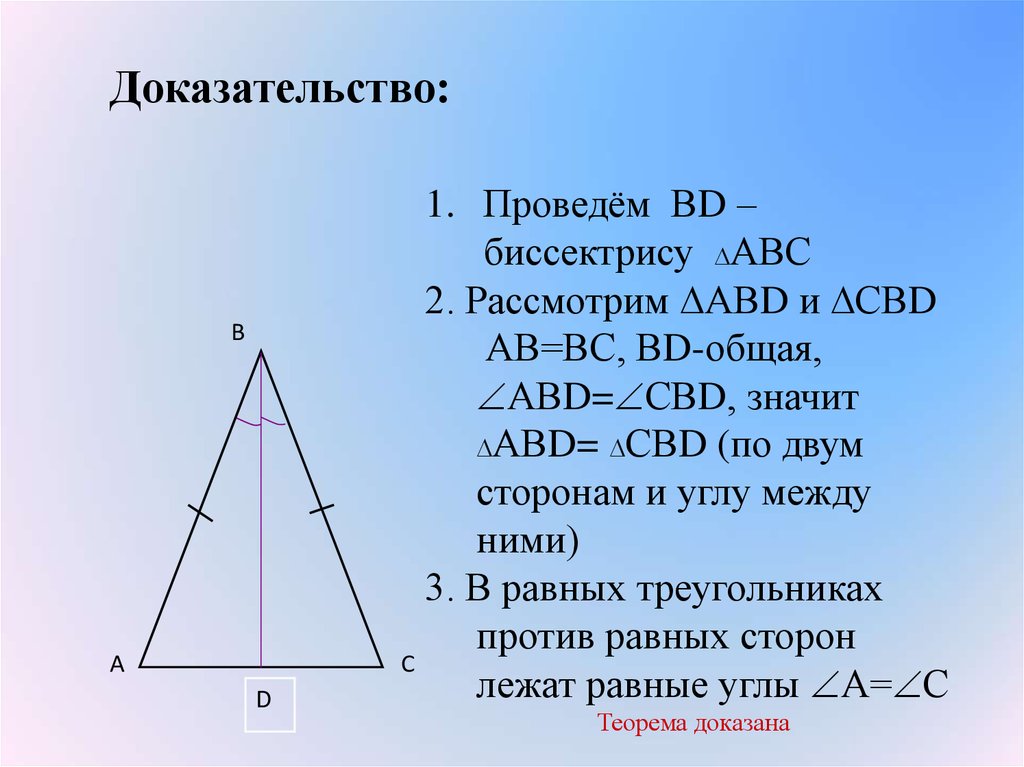
Запомните, что биссектрисой треугольника называется отрезок, который делит угол на два равных угла и соединяет вершину угла с точкой на противоположной стороне.

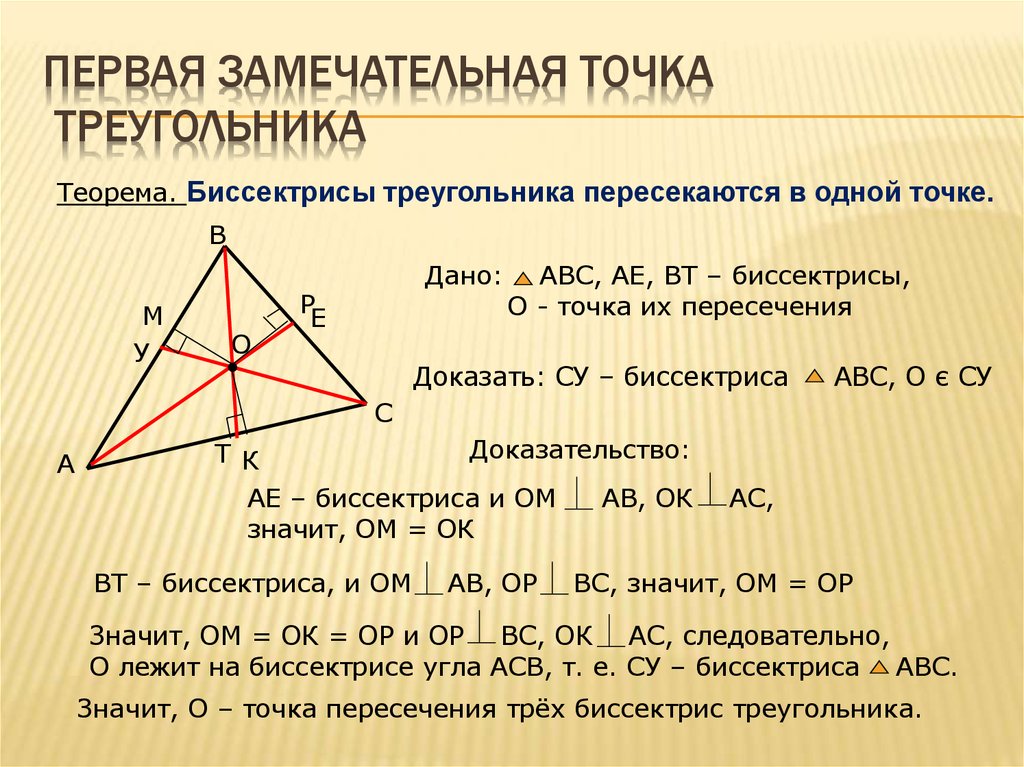
Свойство биссектрисы треугольника с доказательством
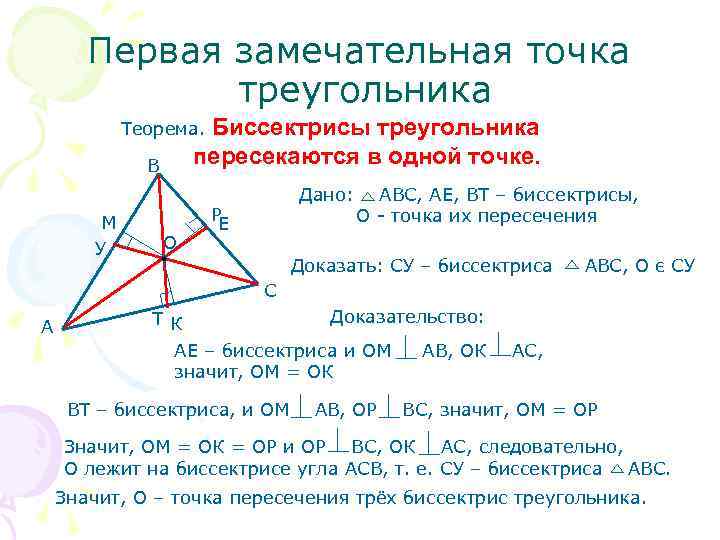
Не забывайте, что в треугольнике биссектрисы всегда пересекаются в одной точке, которая называется инцентром.

Равные треугольники. Высота, медиана, биссектриса треугольника - геометрия 7 класс
При решении задач с теоремой о биссектрисе важно правильно определить, какие углы равны, а также использовать свойства пропорциональности сторон треугольника.

Теорема о биссектрисе треугольника
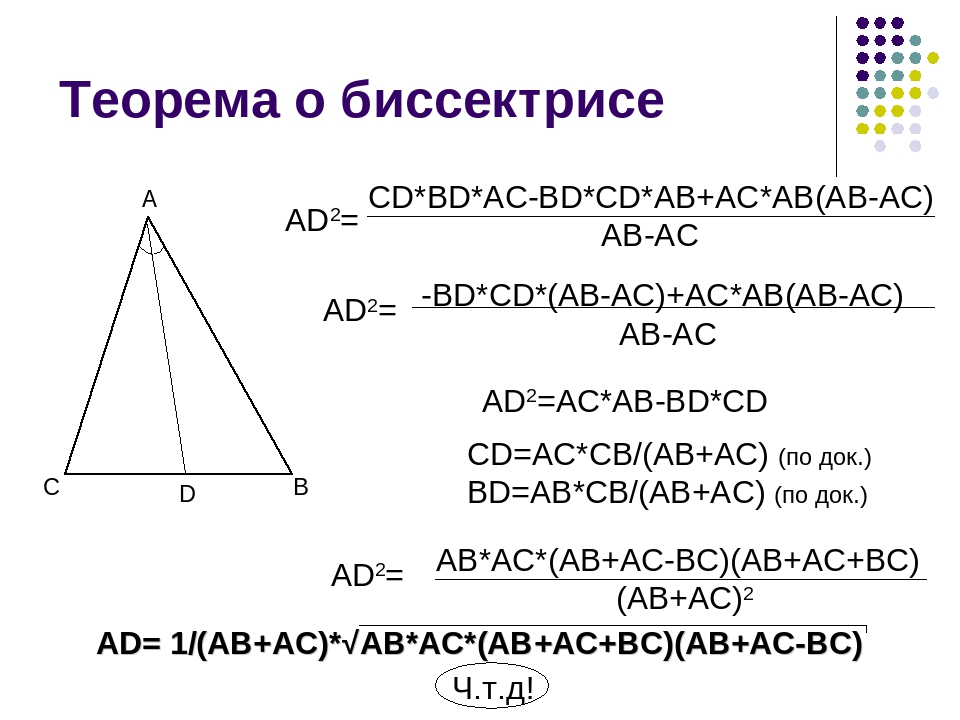
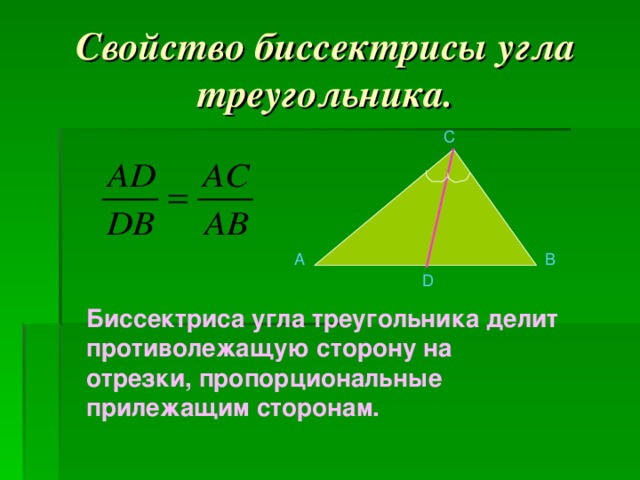
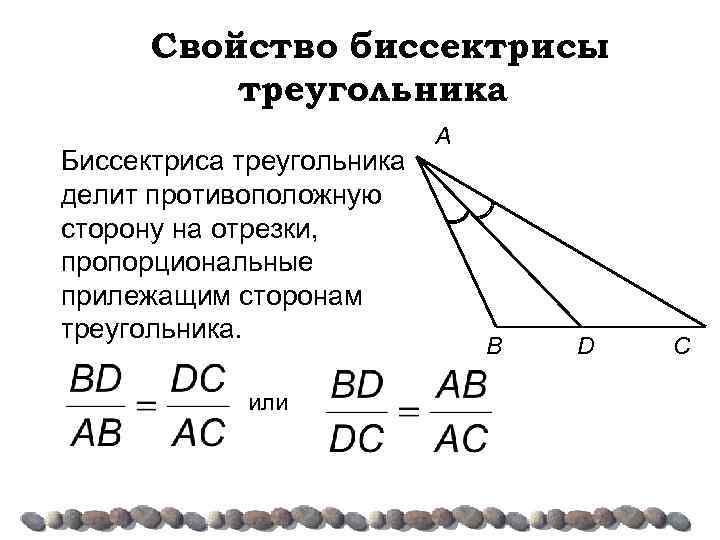
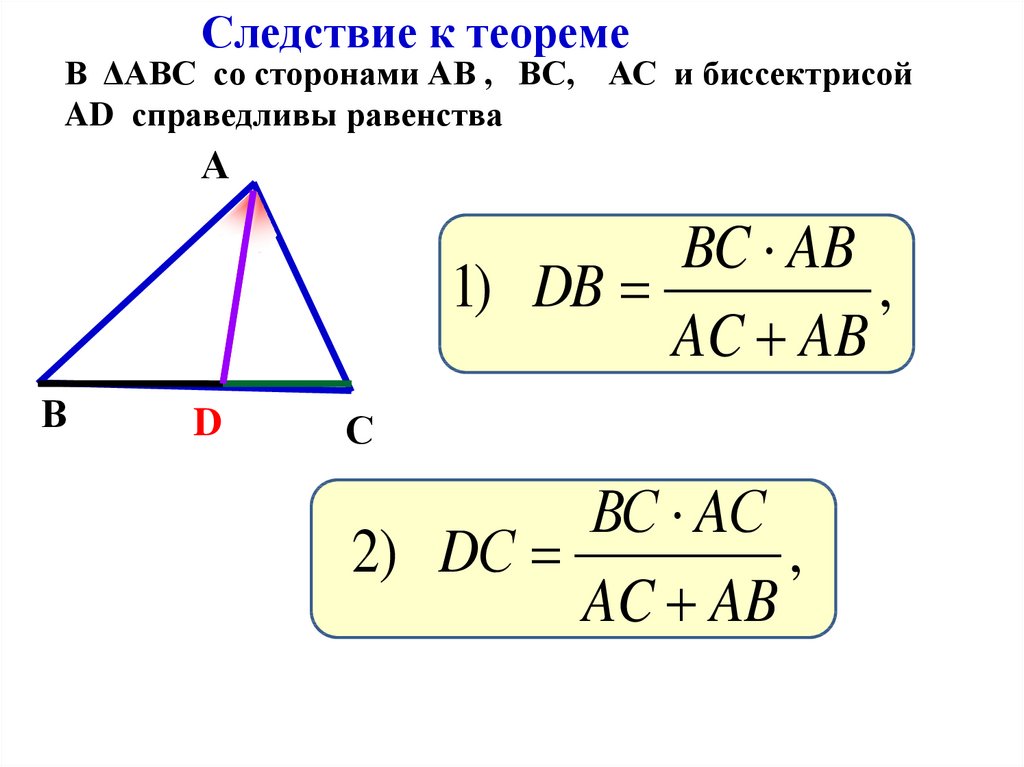
Если задача требует нахождения длины отрезков, образованных биссектрисой, применяйте формулу: (AB / AC) = (BD / DC), где B и C – точки пересечения биссектрисы с противоположной стороной.
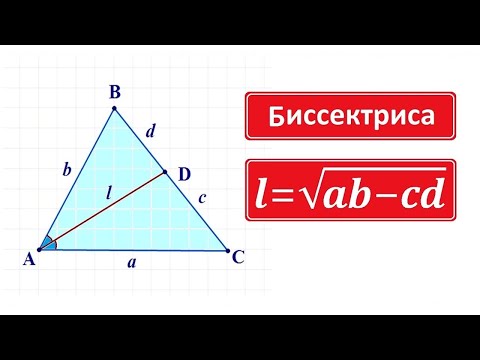
Формула для биссектрисы треугольника
Попрактикуйтесь на задачах, где необходимо использовать теорему о биссектрисе для нахождения расстояний и углов – это укрепит ваше понимание материала.

Свойство биссектрисы треугольника

Запомните, что инцентр треугольника равен точке пересечения всех трех биссектрис, и эта точка всегда лежит внутри треугольника.
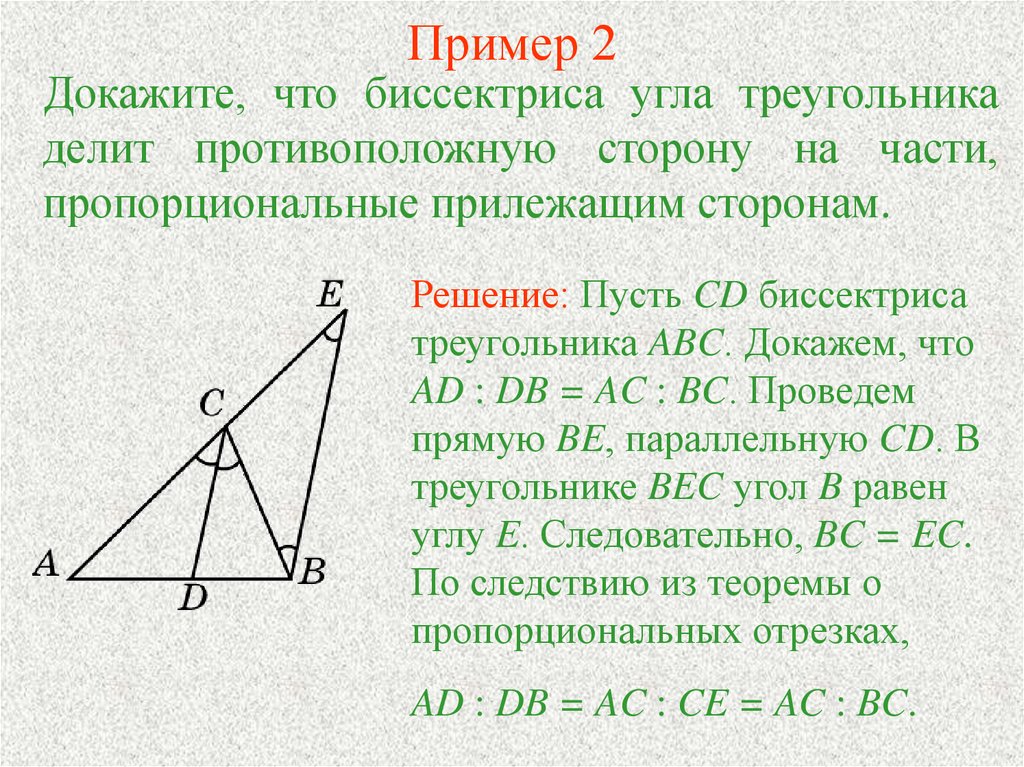

При решении задач на доказательства важно четко следовать логике, показывая, как каждое утверждение вытекает из предыдущего.

БИССЕКТРИСА УГЛА треугольника 8 класс Атанасян
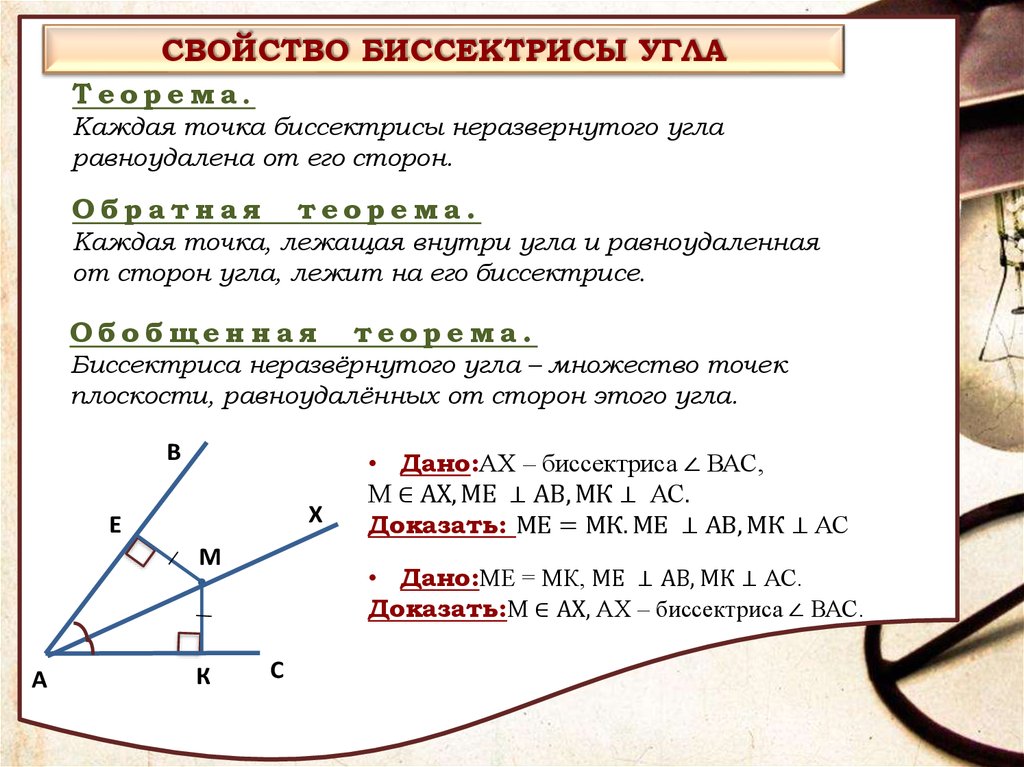
Внимательно читайте условия задачи, чтобы определить, какие данные вам даны и как они связаны с теоремой о биссектрисе.

Урок по теме СВОЙСТВА БИССЕКТРИСЫ УГЛА 8 КЛАСС ГЕОМЕТРИЯ
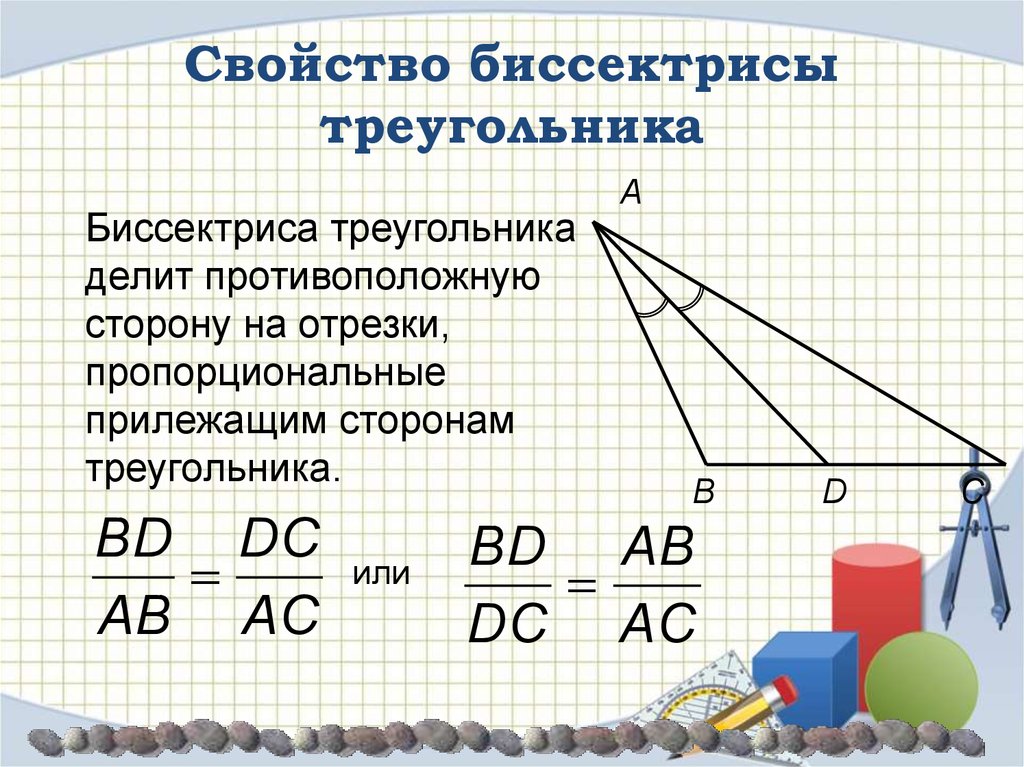
Для улучшения усвоения теоремы рисуйте диаграммы и отмечайте все ключевые элементы – это поможет визуализировать задачу.

11 класс, 46 урок, Теорема о биссектрисе треугольника
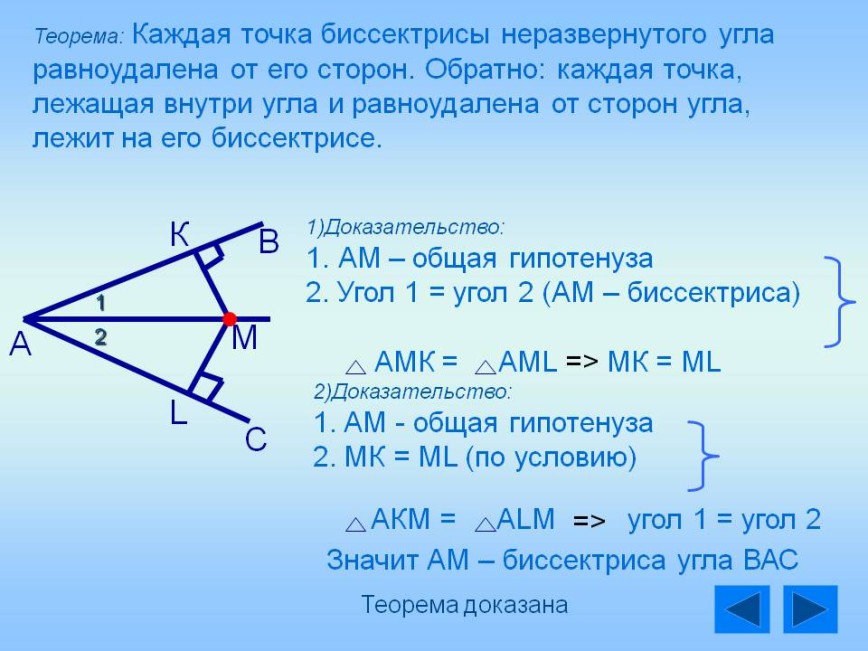
Не забывайте про симметрию треугольников, так как это может значительно упростить решение задач, связанных с биссектрисами.


Реакция на результаты ЕГЭ 2022 по русскому языку