Все о средней линии треугольника: простое объяснение и советы
Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника. Она обладает уникальными свойствами: параллельна основанию и равна его половине. Знание средней линии полезно как в геометрии, так и в практических задачах.

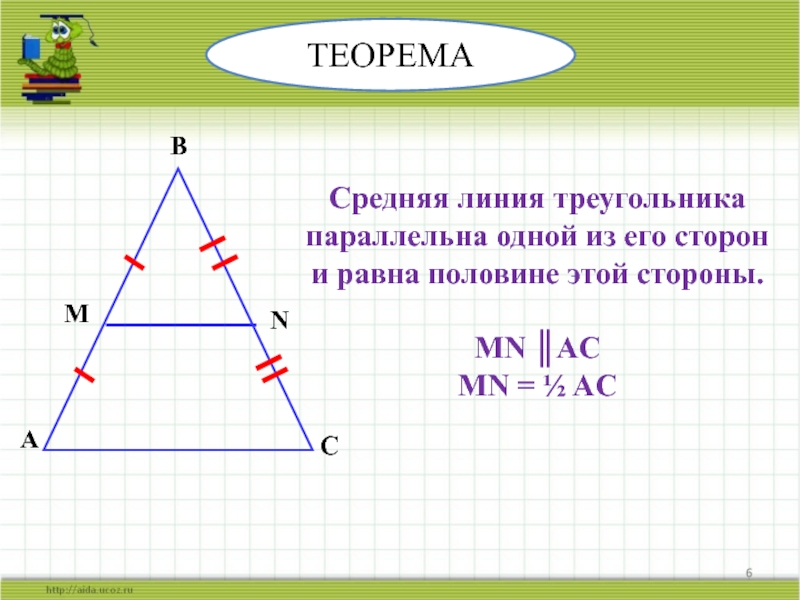
Чтобы найти среднюю линию треугольника, начертите отрезок, соединяющий середины двух сторон.

Теорема о средней линии треугольника. Доказательство. 8 класс.


Средняя линия всегда параллельна третьей стороне треугольника — используйте это свойство для проверки чертежа.

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном Треугольнике

Зная длину основания, легко определить длину средней линии: она равна половине основания.
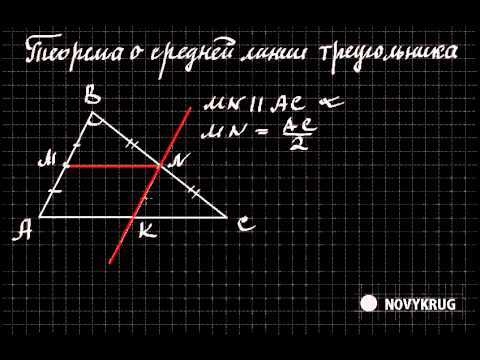
Теорема о средней линии треугольника
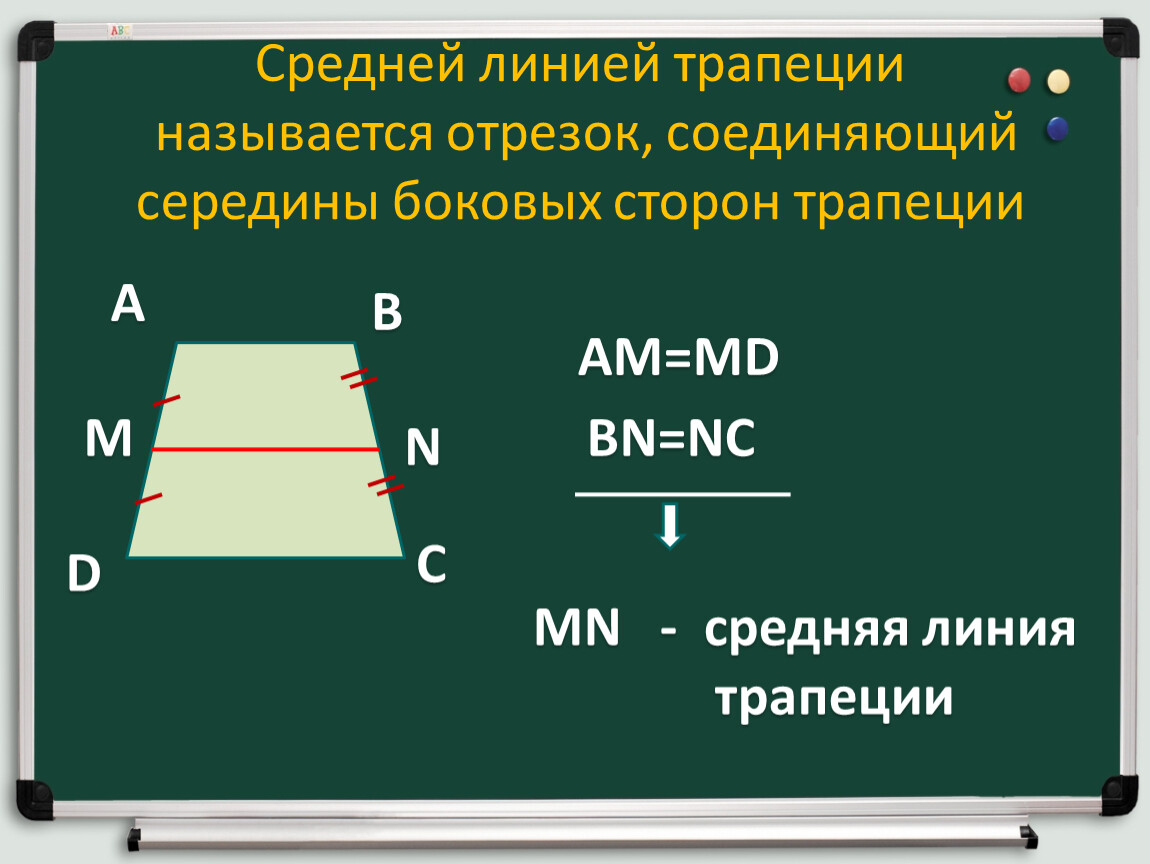
Средняя линия делит треугольник на два равновеликих треугольника.

Задача 484 Атанасян Геометрия 7-9 2024

Используйте среднюю линию для упрощения расчетов в задачах на площади треугольников.

Средняя линия треугольника. Задачи по готовым чертежам
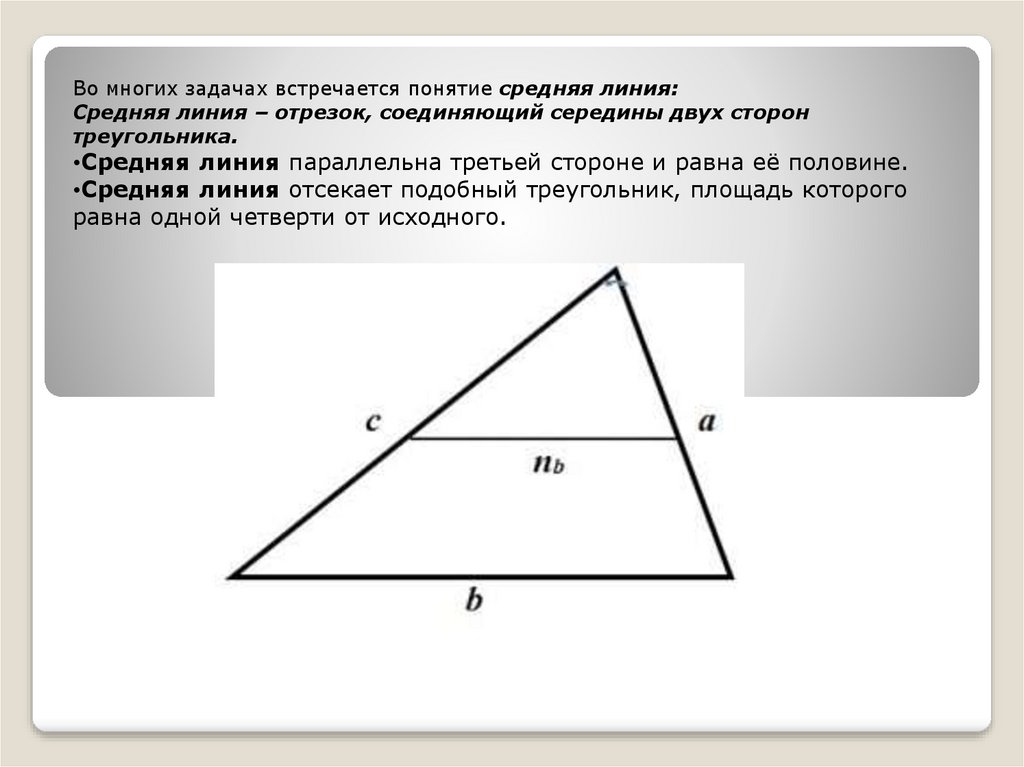
При построении средней линии точно определяйте середины сторон с помощью циркуля или линейки.

Найдите сторону треугольника на рисунке

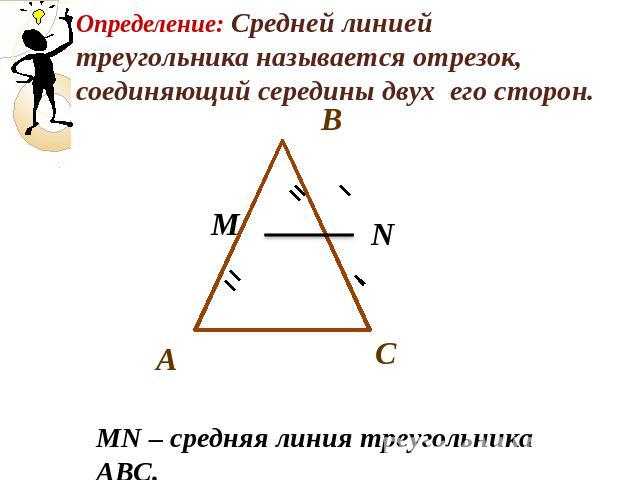
Если требуется доказать свойства средней линии, используйте теорему Фалеса и параллельность прямых.
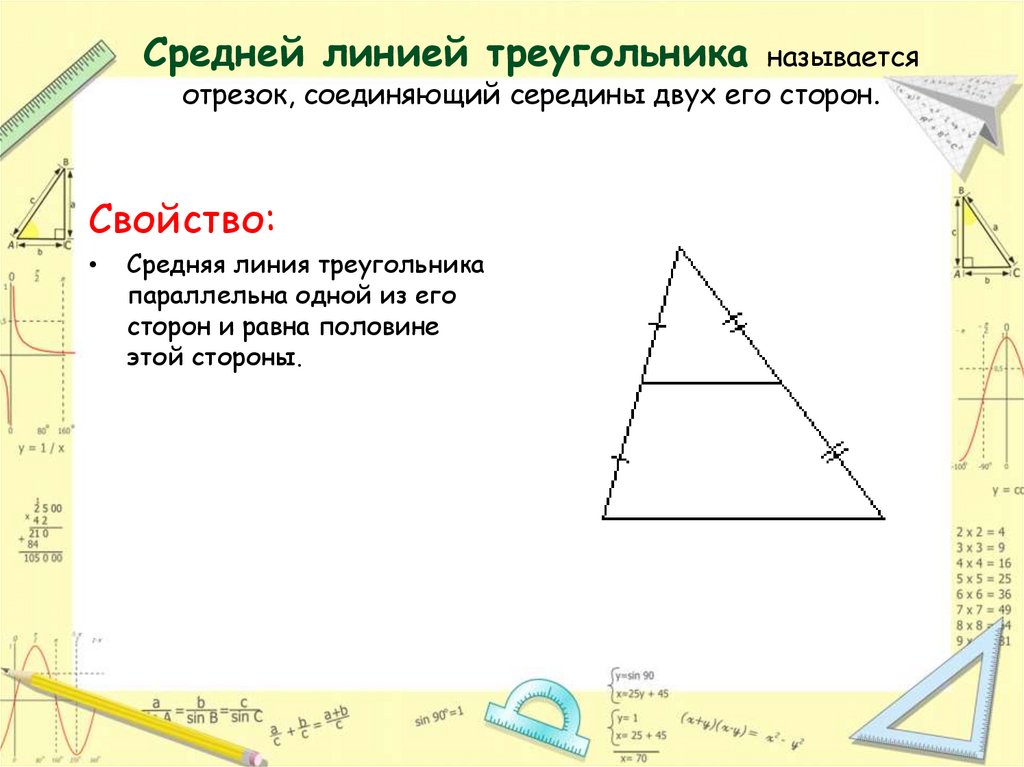

Средняя линия упрощает задачи на нахождение координат точек в треугольнике.

Средняя линия треугольника и трапеции. 8 класс.

8 класс, 25 урок, Средняя линия треугольника
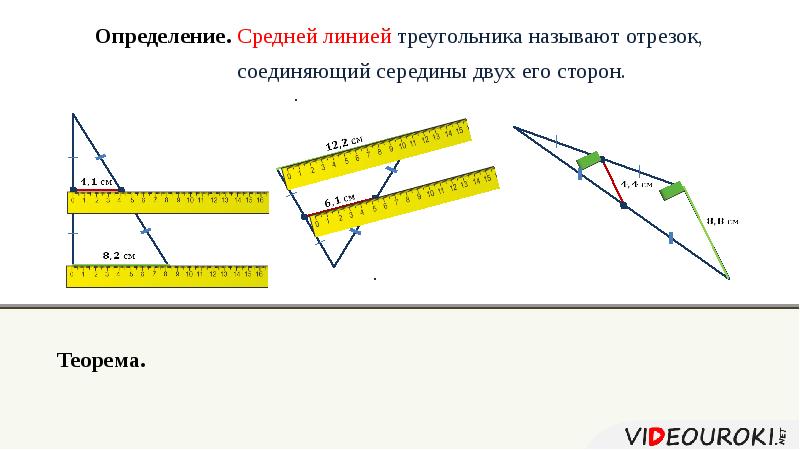
В прямоугольном треугольнике средняя линия, проведенная к гипотенузе, равна половине гипотенузы.

Средняя линия треугольника – 8 класс геометрия
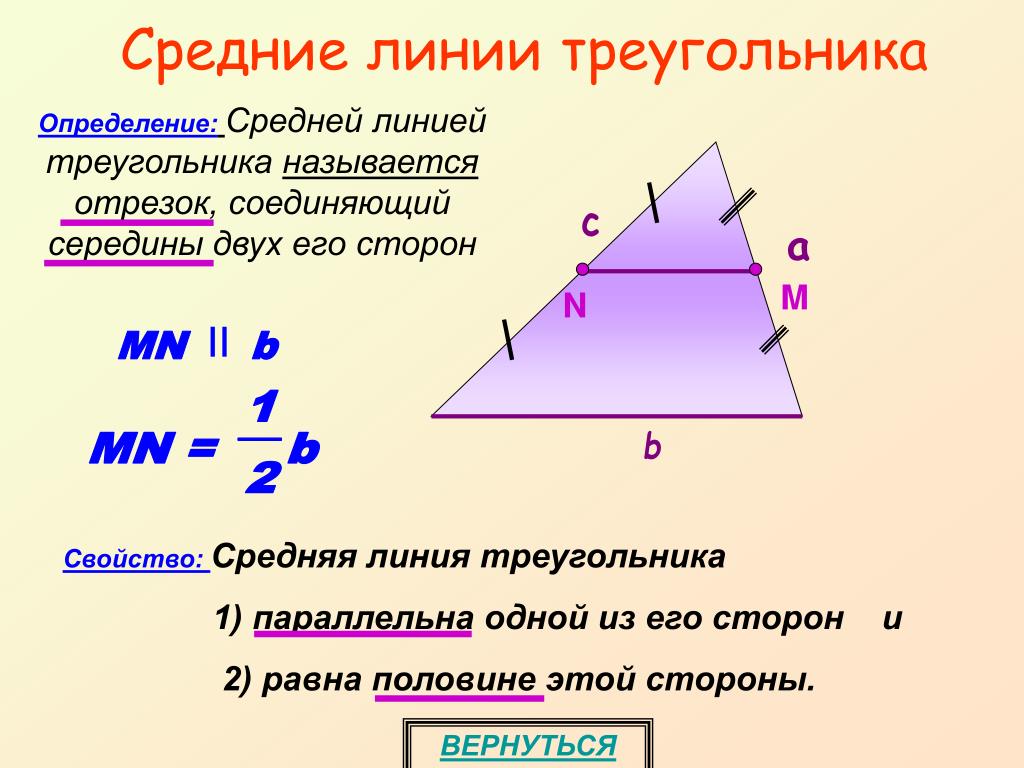
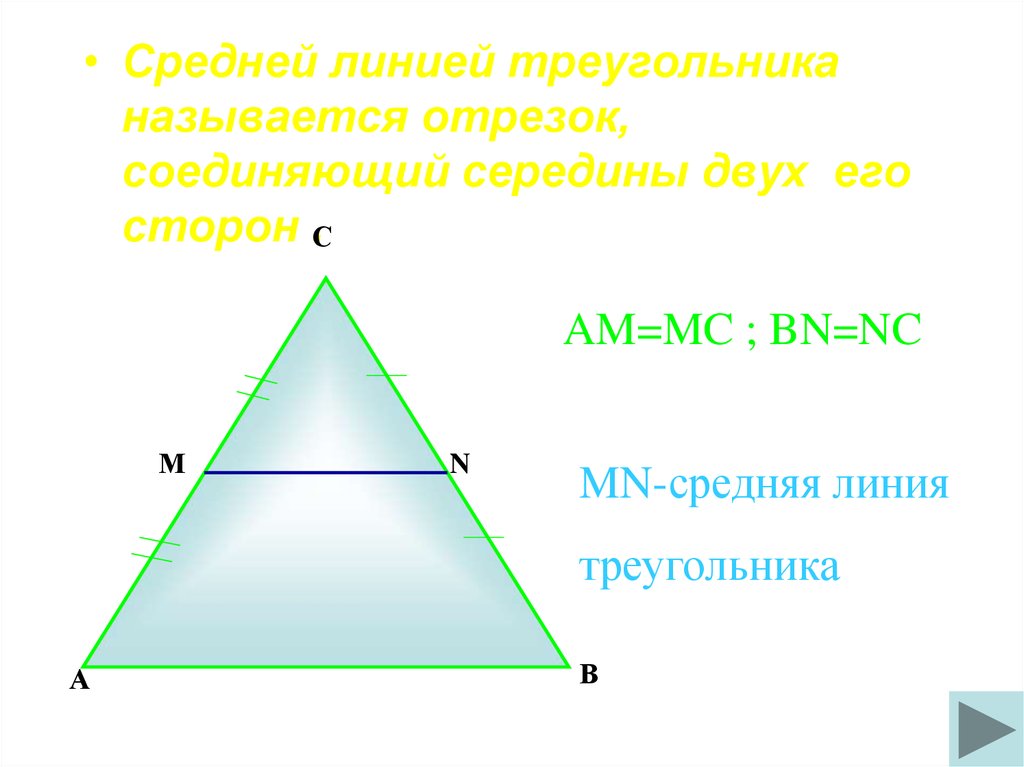
Изучайте свойства средней линии, чтобы эффективно решать задачи по геометрии и стереометрии.
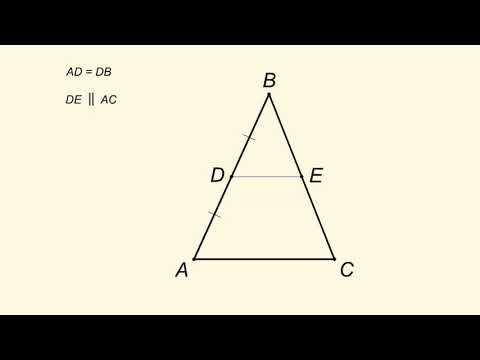
Средняя линия. Теорема о средней линии треугольника
