Как определить смежные отрезки в многоугольниках и какие они имеют свойства?
Смежные отрезки многоугольника — это два отрезка, которые соединяются в одной вершине, являясь частью одной стороны этого многоугольника. Важно уметь правильно идентифицировать такие отрезки, чтобы понимать их геометрическое расположение и отношения между элементами многоугольника.
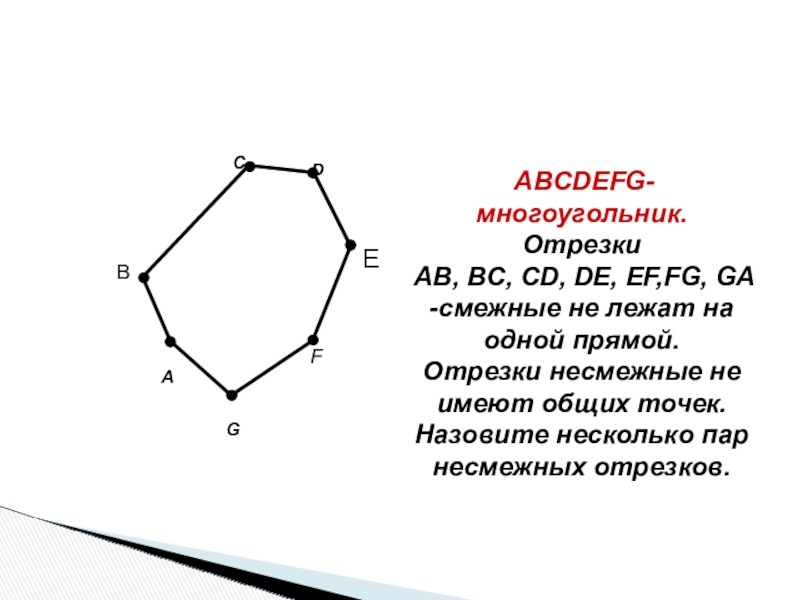
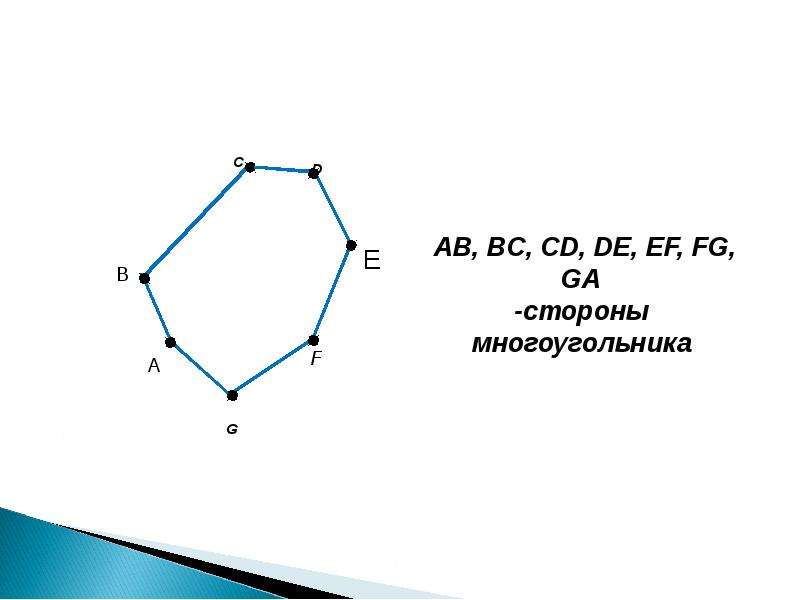
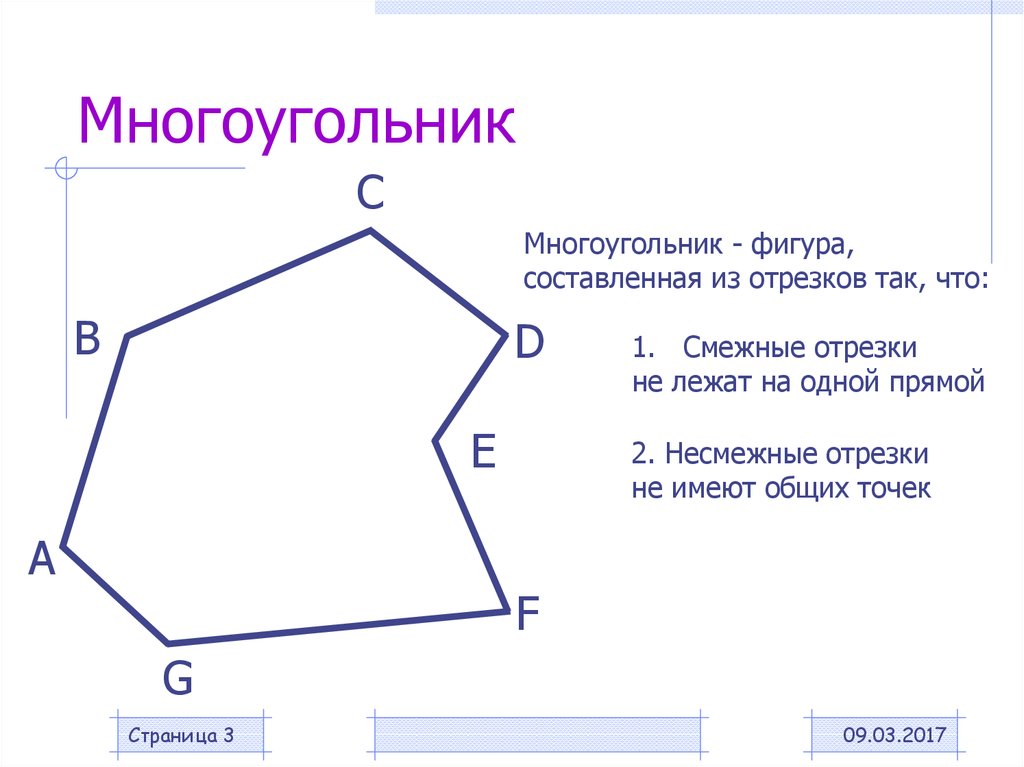
Смежные отрезки всегда будут находиться рядом и иметь общую вершину. Запомните, что их не следует путать с параллельными отрезками, которые могут не соприкасаться.

Многоугольники. 8 класс.
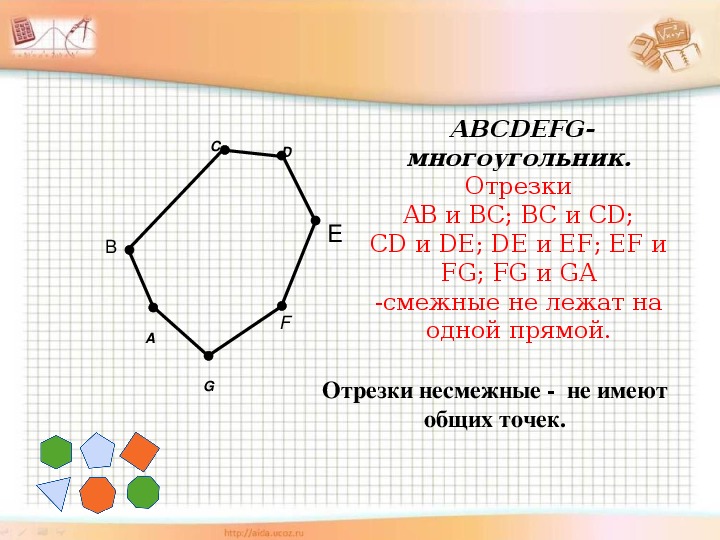
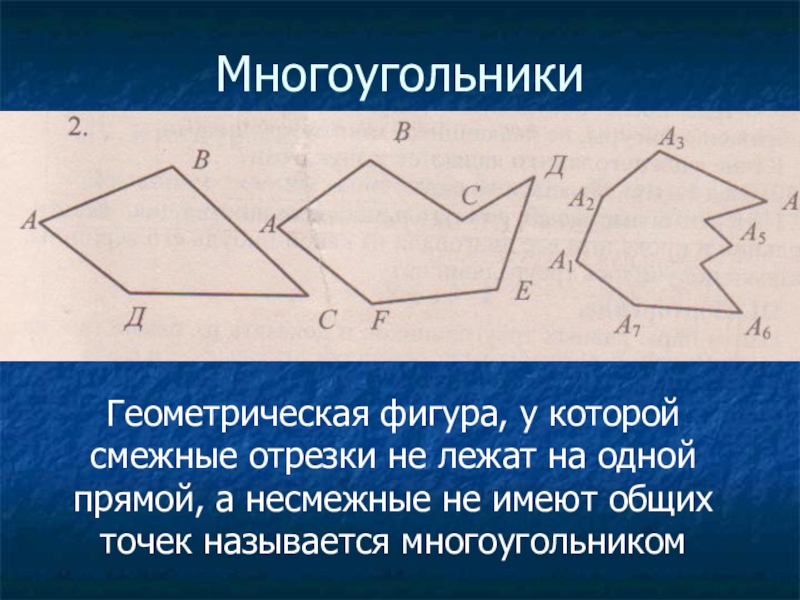
При изучении многоугольников обращайте внимание на количество смежных отрезков в каждой вершине: для простых многоугольников это обычно два отрезка, но в случае с многоугольниками более высокой степени может быть и больше.

Многоугольники #13

Помните, что смежные отрезки могут образовывать углы, важные для вычислений в геометрии. Знание их свойств поможет в дальнейшем решении задач.

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы - Математика TutorOnline

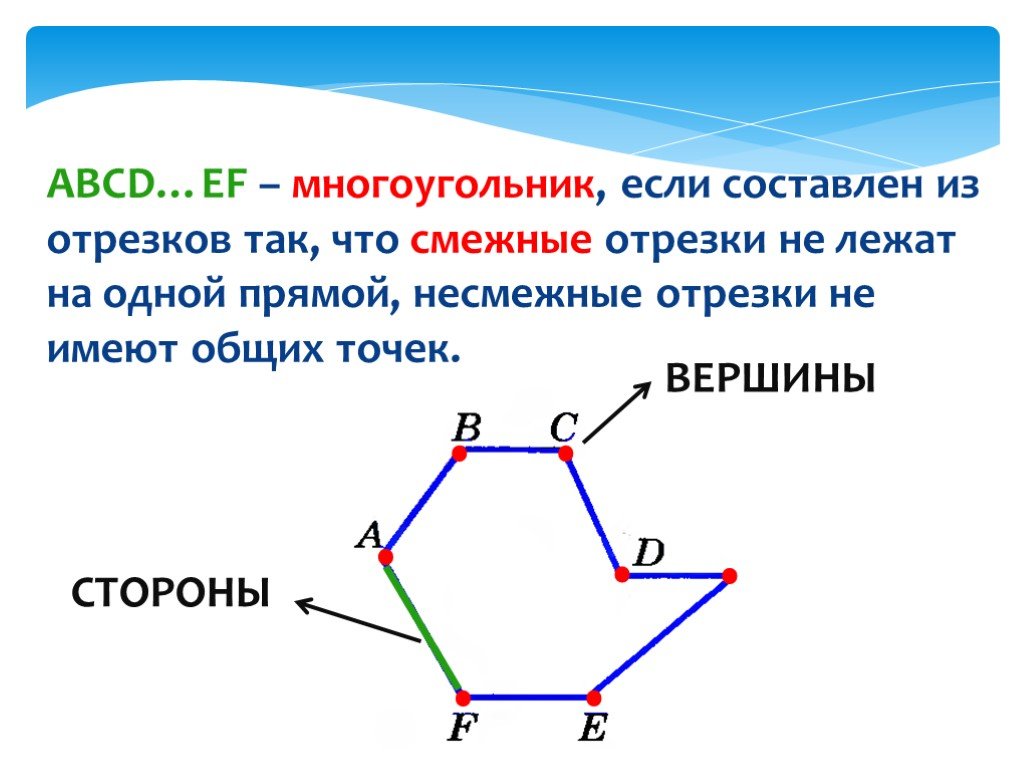
Для правильного нахождения смежных отрезков полезно визуализировать многоугольник, что поможет точнее определить, какие отрезки являются соседними и какие углы они образуют.

Многоугольники. Математика 8 класс - TutorOnline
Не забывайте, что в многоугольниках с большим количеством сторон (например, в десятиугольниках и более) смежные отрезки могут быть расположены неравномерно, что следует учитывать при анализе.

Многоугольник
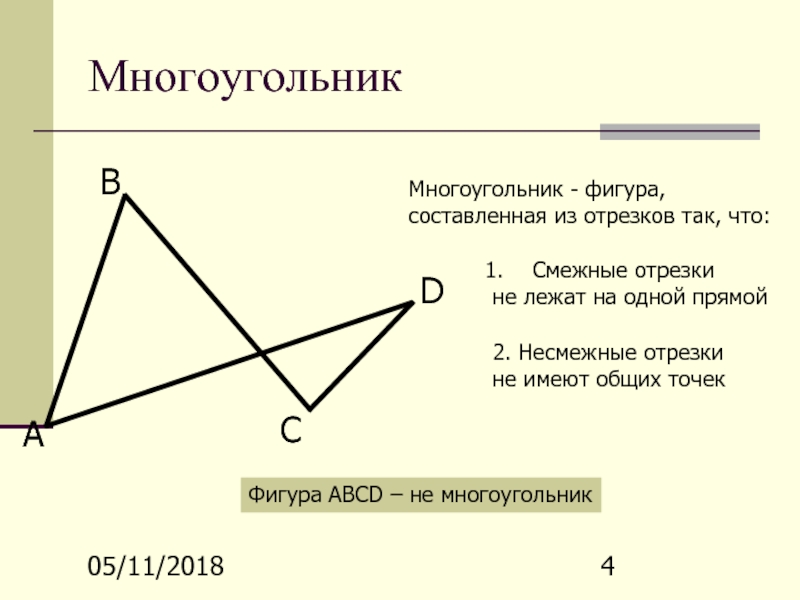
При решении задач по геометрии часто требуется найти угол между смежными отрезками. Для этого можно использовать свойства углов в многоугольниках или формулы для вычисления углов.

Для понимания структуры многоугольников полезно помнить, что смежные отрезки могут быть равными, если стороны многоугольника равны по длине, как в случае с правильными многоугольниками.
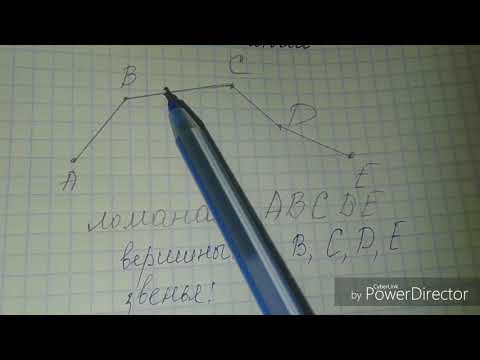
Ломаная


Если многоугольник состоит из прямых углов, то все смежные отрезки образуют углы в 90 градусов, что является важной характеристикой прямоугольных многоугольников.

Многоугольники. Четырёхугольник

Геометрия 8 класс. Многоугольники
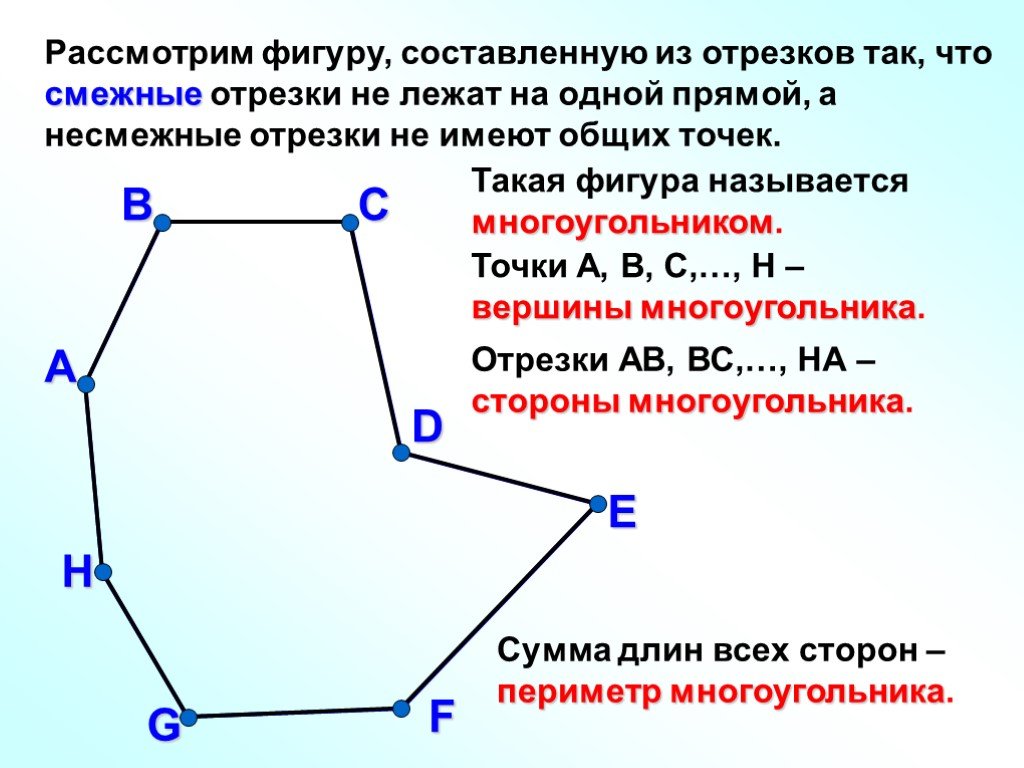
Смежные отрезки можно использовать для вычисления периметра многоугольника, если известны длины его сторон и их количество.

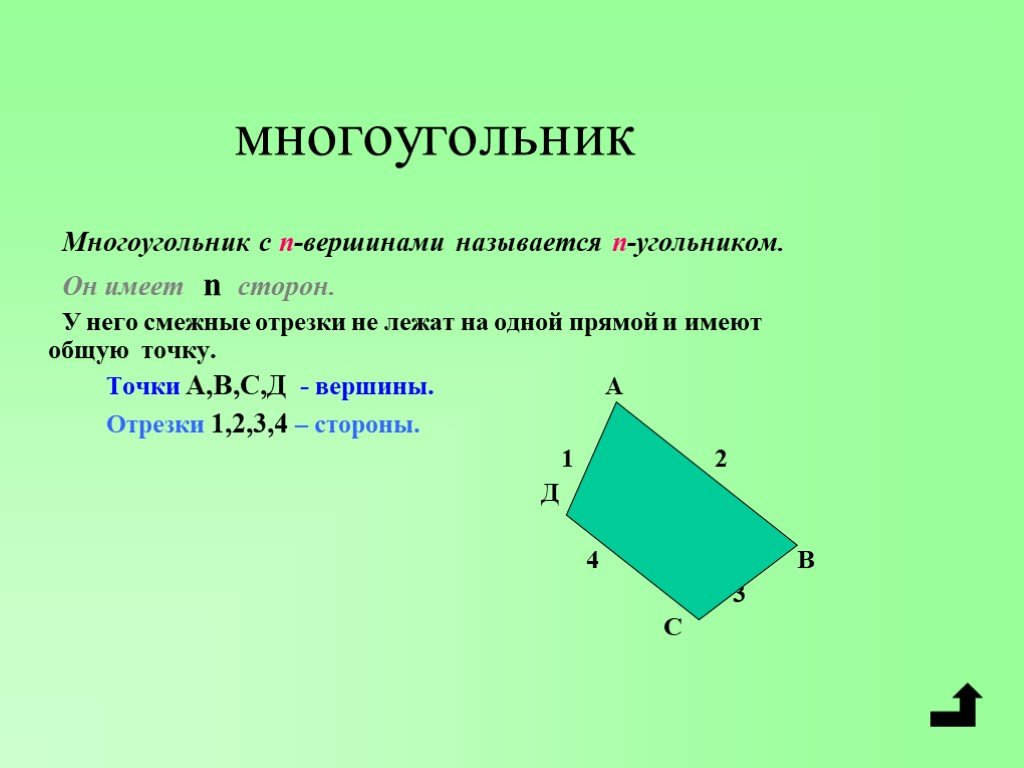
Чтобы лучше понять взаимосвязь между смежными отрезками, пробуйте рисовать различные многоугольники, отмечая их вершины и соединения, что помогает увидеть их расположение и связи на практике.