Как понять симметрию куба относительно точки: полезные советы и примеры
Симметрия куба относительно точки — это важный концепт в геометрии и 3D-моделировании. Эта симметрия играет ключевую роль в изучении пространственных объектов, а также используется в различных областях, от математики до искусства. В этой подборке мы разберем основные принципы симметрии куба, приведем примеры и поделимся полезными советами для эффективного освоения этого материала.
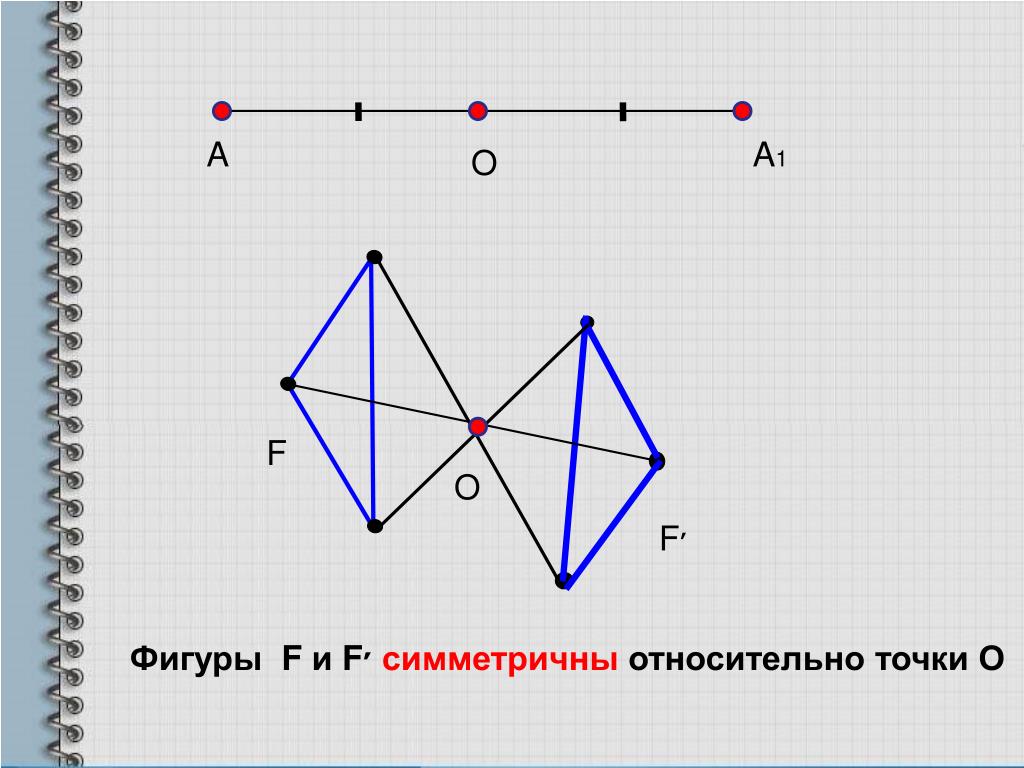
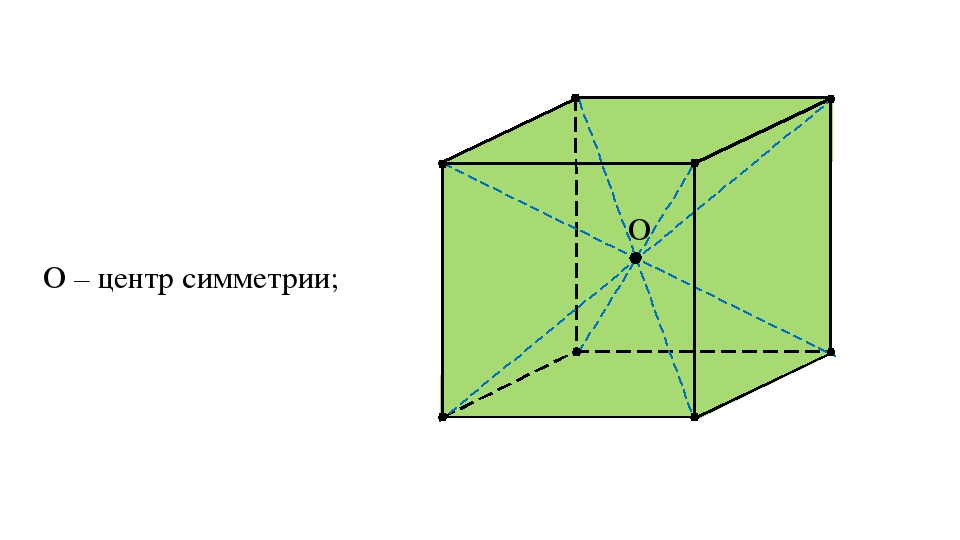
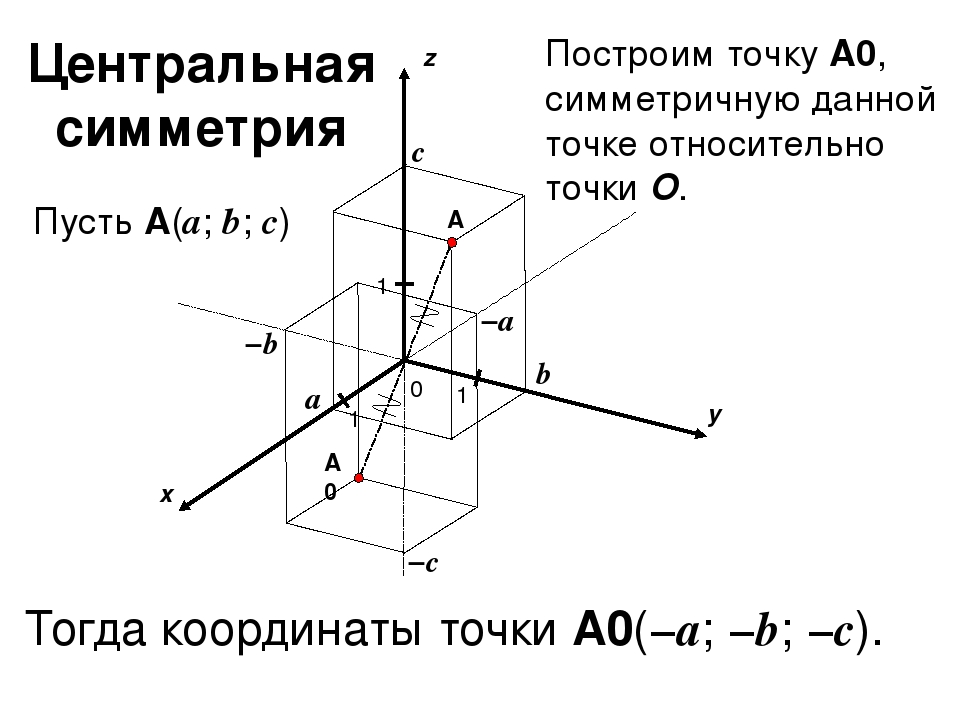
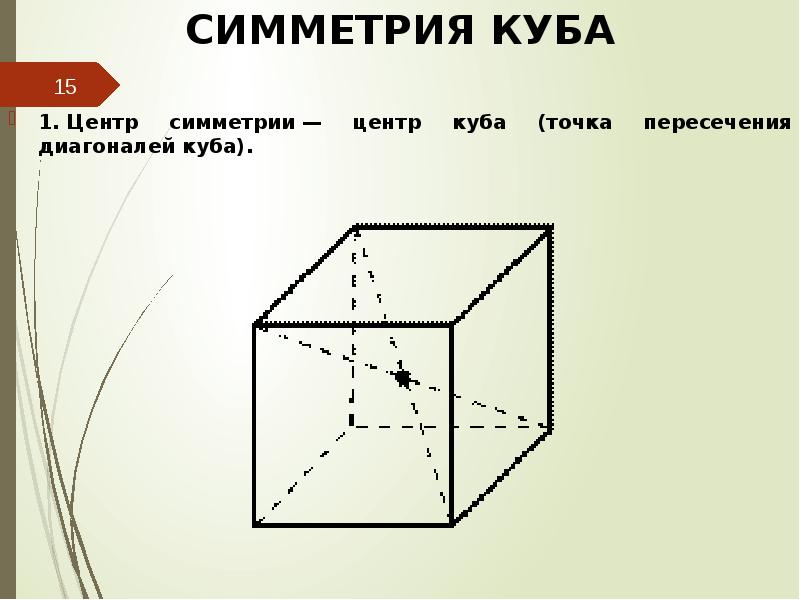
При изучении симметрии куба важно понимать, что центральная точка является осью симметрии для всех его граней и вершин.

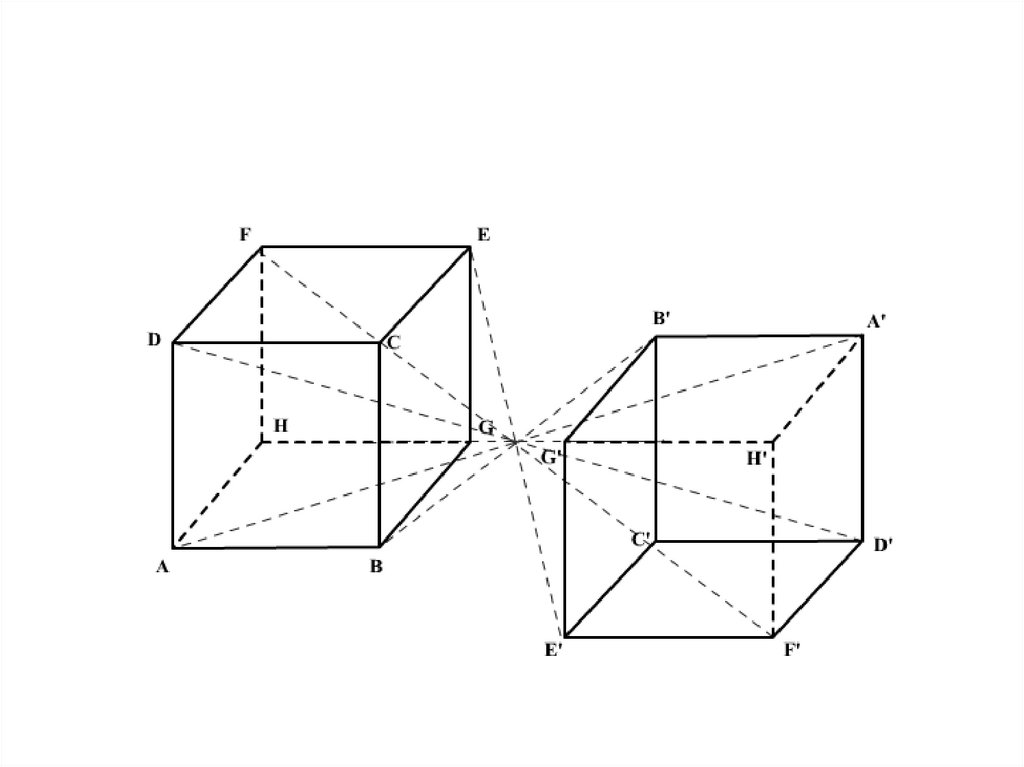
Симметрия относительно точки (центральная симметрия). Пример 2
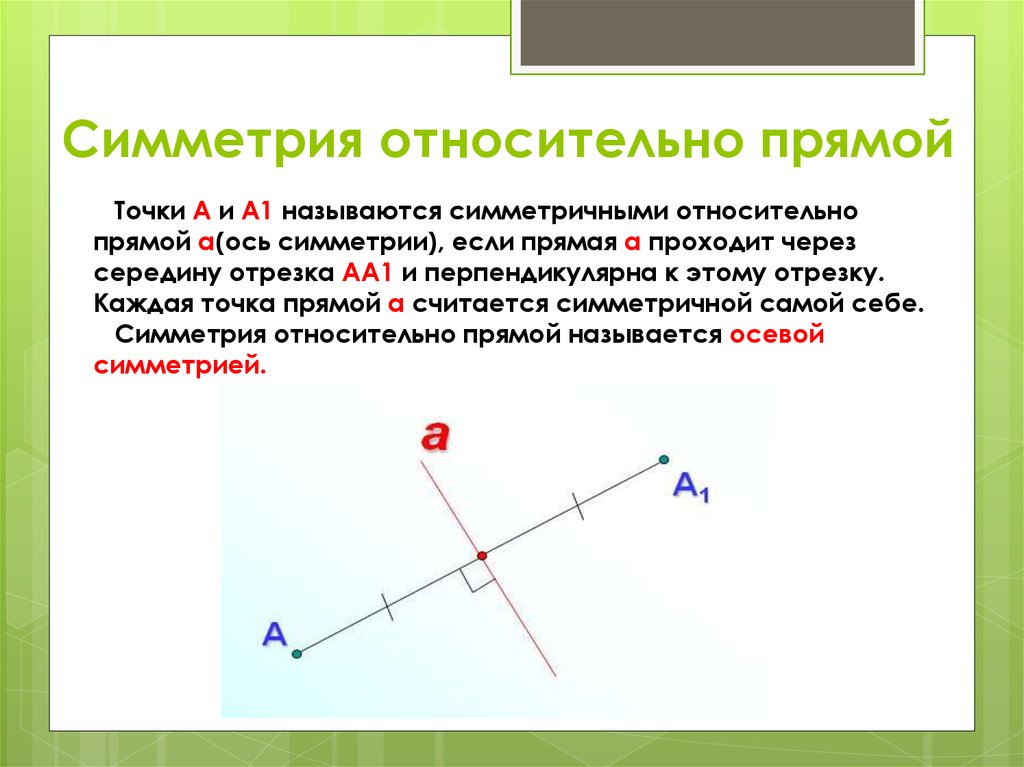
Для точного определения симметрии куба относительно точки попробуйте провести оси симметрии через его центр и проверить, как меняются координаты точек после отражения.

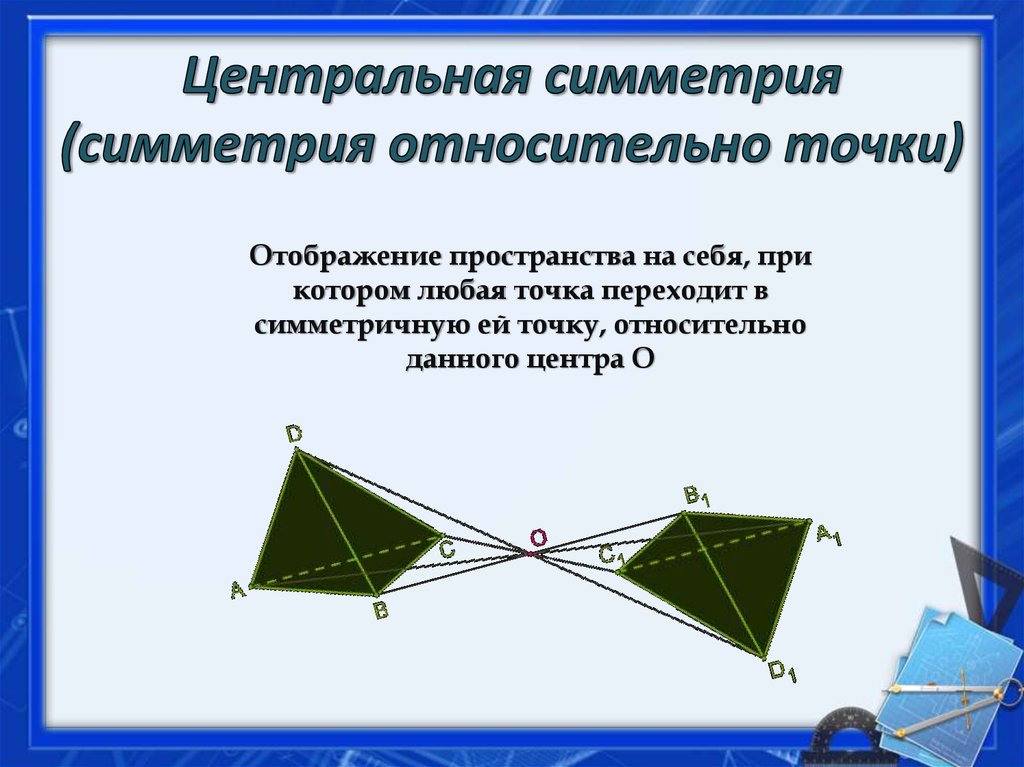
Симметрия относительно точки. 6 класс
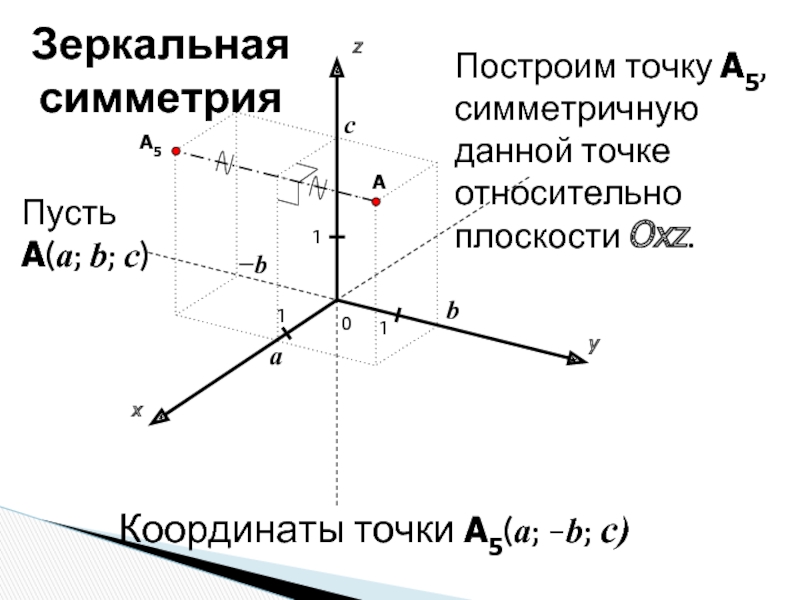
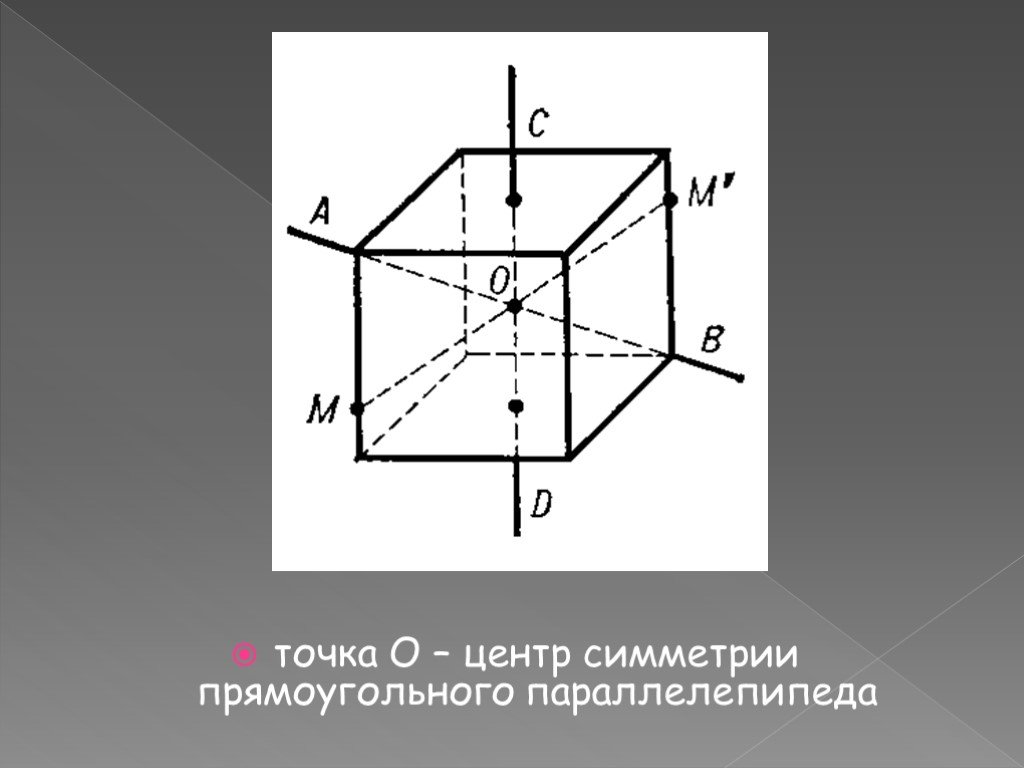
Если вы используете 3D-редактор для моделирования, обратите внимание на инструменты зеркалирования, которые могут помочь вам быстро реализовать симметрию относительно заданной точки.

Геометрия 8 класс. Осевая и центральная симметрия
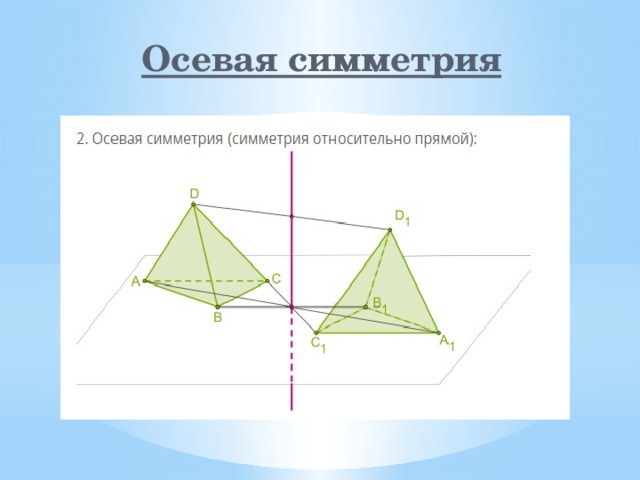
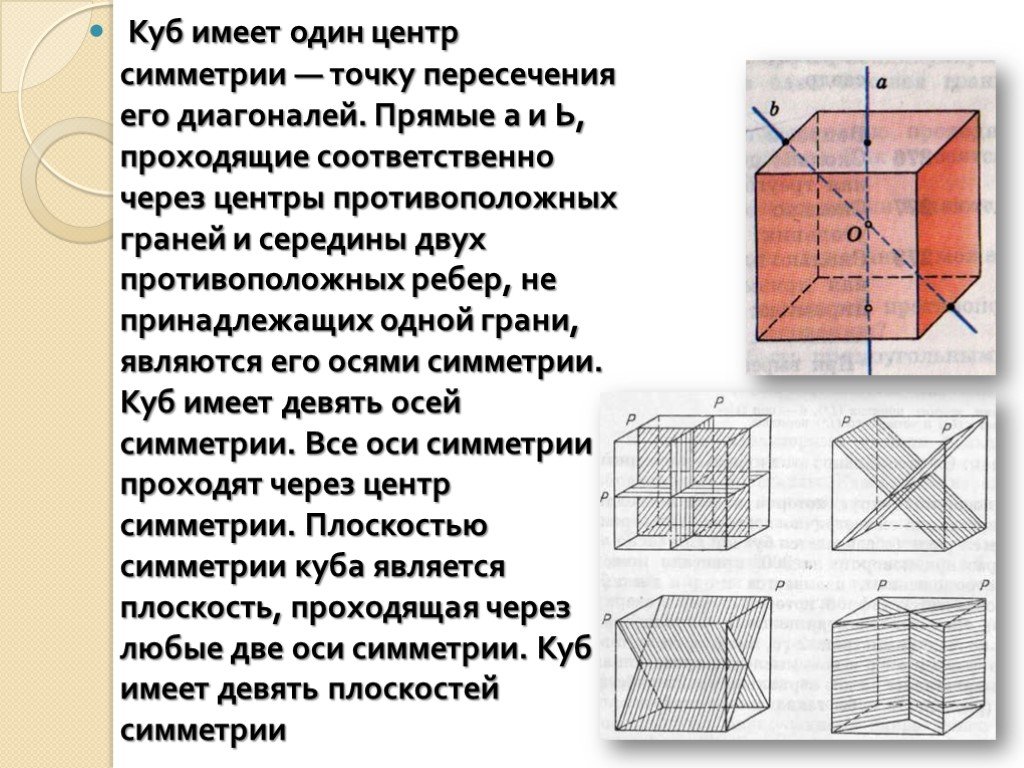
Чтобы лучше понять симметрию куба, нарисуйте его на бумаге, выделив центральную точку, и отразите все элементы относительно этой точки.

Математика. 6 класс. Центральная и осевая симметрии /15.03.2021/


Симметрия куба относительно точки также используется в некоторых видах головоломок, например, в кубиках Рубика, где важно ориентировать элементы относительно центра.

Что такое центр симметрии #огэ #математика #shorts
Помните, что симметрия куба может быть выполнена не только в пространстве, но и на плоскости — рассмотрите проекции куба для изучения его симметрии.
При работе с симметрией в программировании, для выполнения отражения объектов относительно точки можно использовать алгоритмы трансформации координат.

Элементы симметрии куба. cubic 9m sym 2


Обратите внимание, что каждая из вершин куба имеет противоположную ей вершину, и именно эта пара определяет ось симметрии относительно центральной точки.
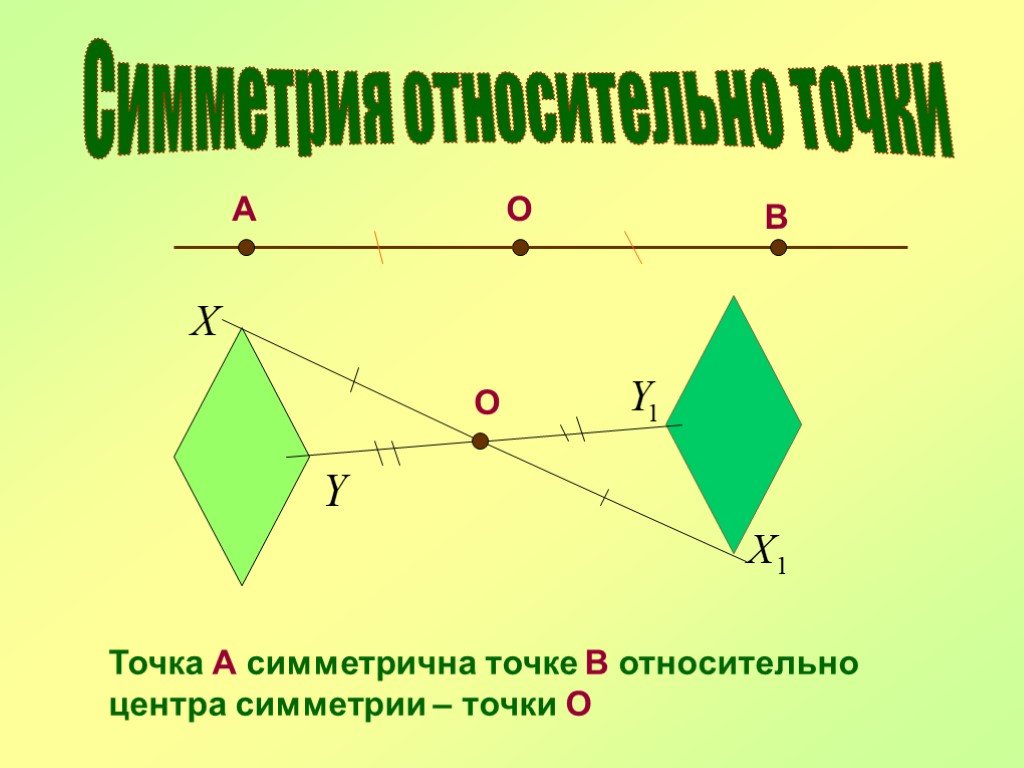
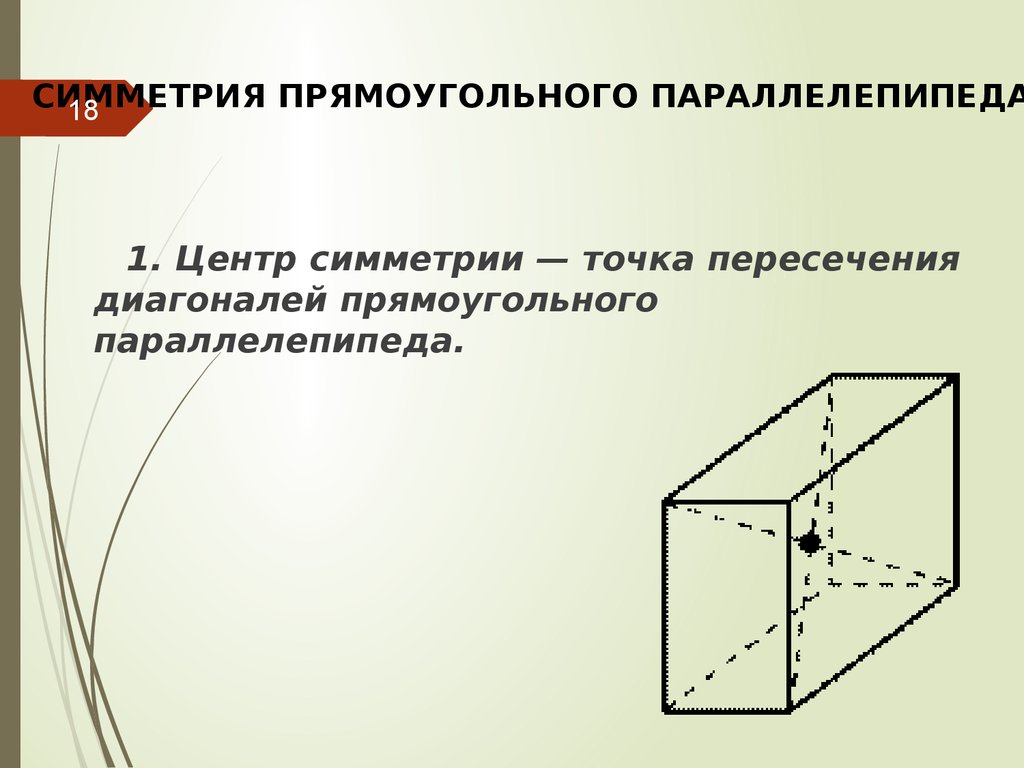
Понять симметрию куба можно через его диагонали: они пересекаются в центре куба, разделяя его на одинаковые части.
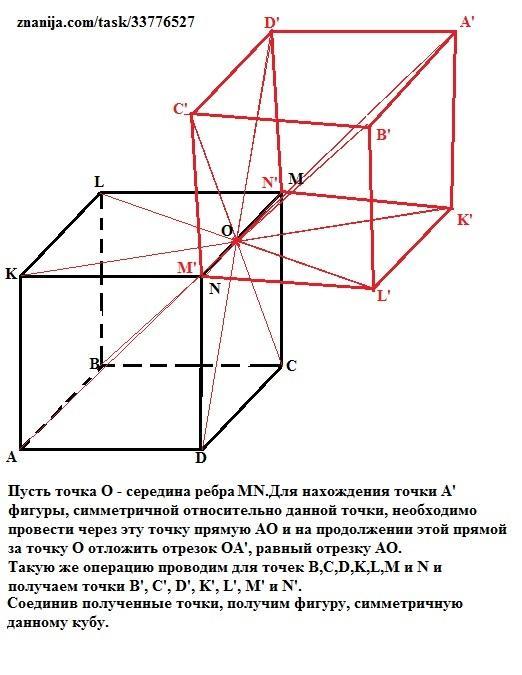
Используйте модели кубов, созданные в 3D-графике, чтобы наглядно увидеть, как работает симметрия относительно центра объекта.
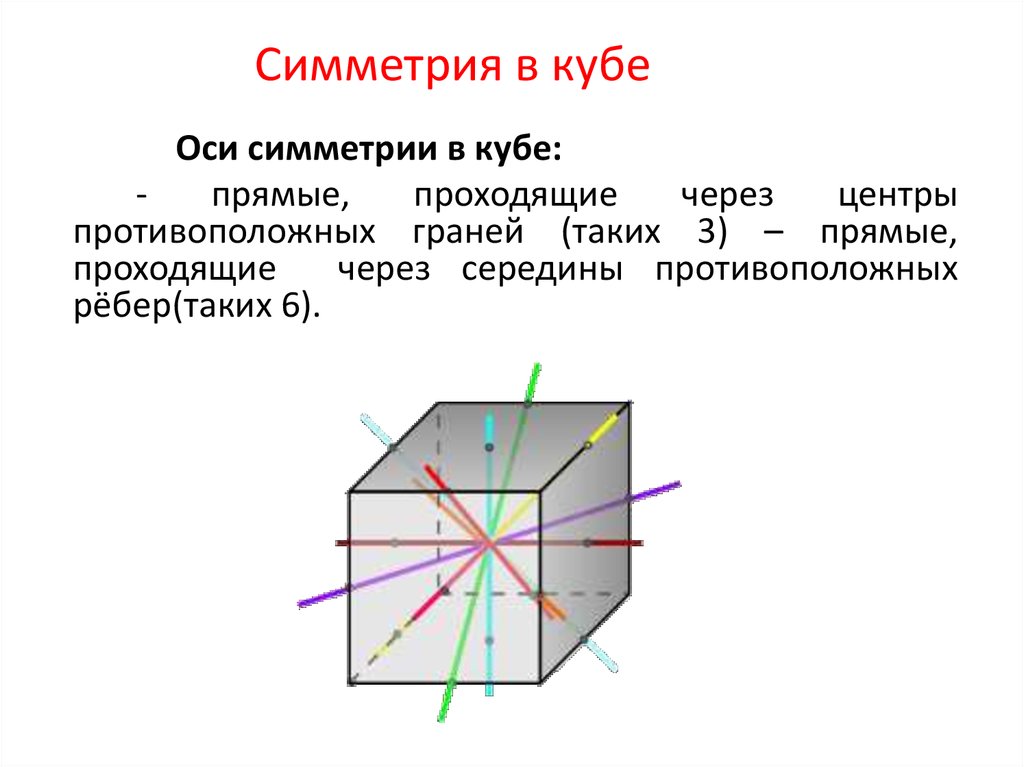

8 класс, 9 урок, Осевая и центральная симметрия