Как вычислить радиус графа, используя его матрицу смежности: подробное объяснение
Радиус графа — это важная характеристика, которая используется в теории графов для анализа структуры сети. В данном разделе мы рассмотрим, как можно вычислить радиус графа, применяя его матрицу смежности. Пошаговое руководство и советы помогут вам понять основные принципы работы с графами и эффективно применять их на практике.

Для начала убедитесь, что ваша матрица смежности корректно отражает связи между вершинами графа.

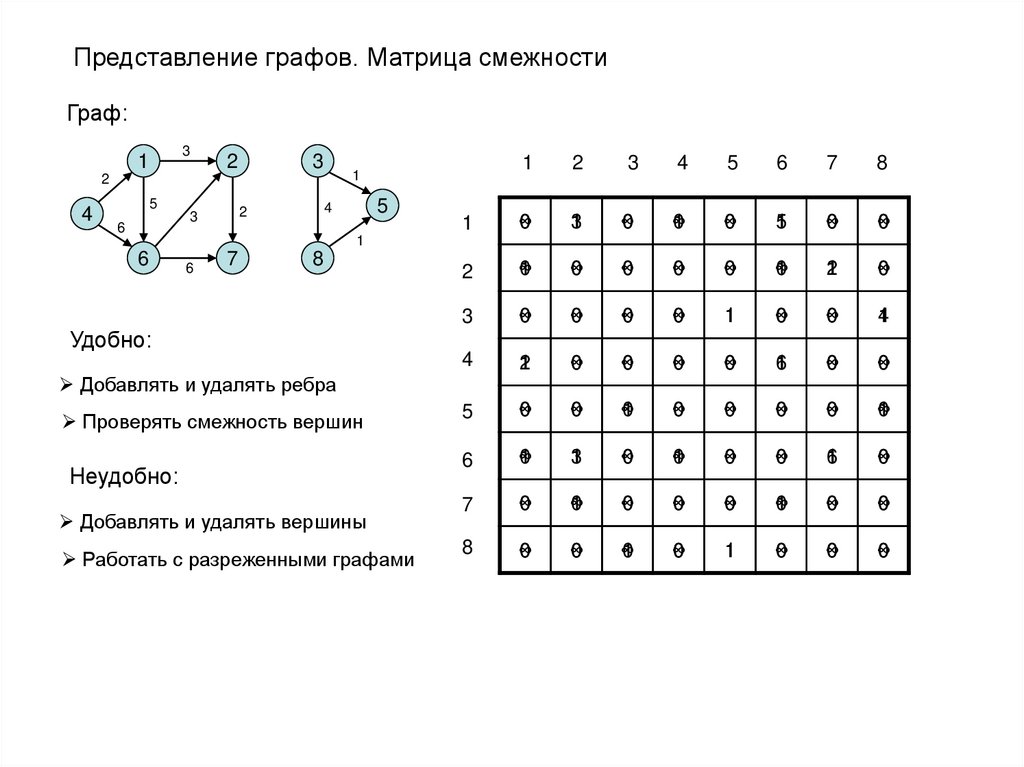
Способы представления графов: список рёбер, матрица смежности, списки смежности

Применяйте алгоритмы поиска кратчайших путей, такие как алгоритм Флойда, для вычисления расстояний между всеми вершинами.
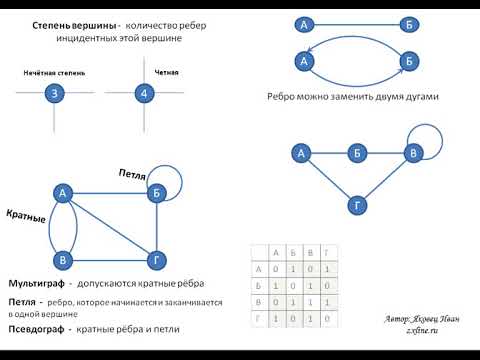
Графы, вершины, ребра, инцидентность, смежность
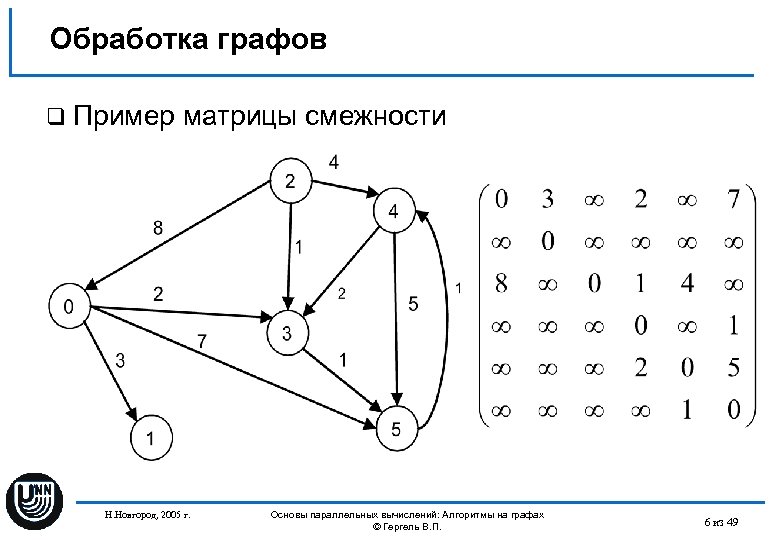
После того как вы получите все кратчайшие расстояния, вычислите диаметр графа, который представляет собой максимальное расстояние между любыми двумя вершинами.
Хранение графов (часть 1) - три базовых метода. Очень просто и с примерами.
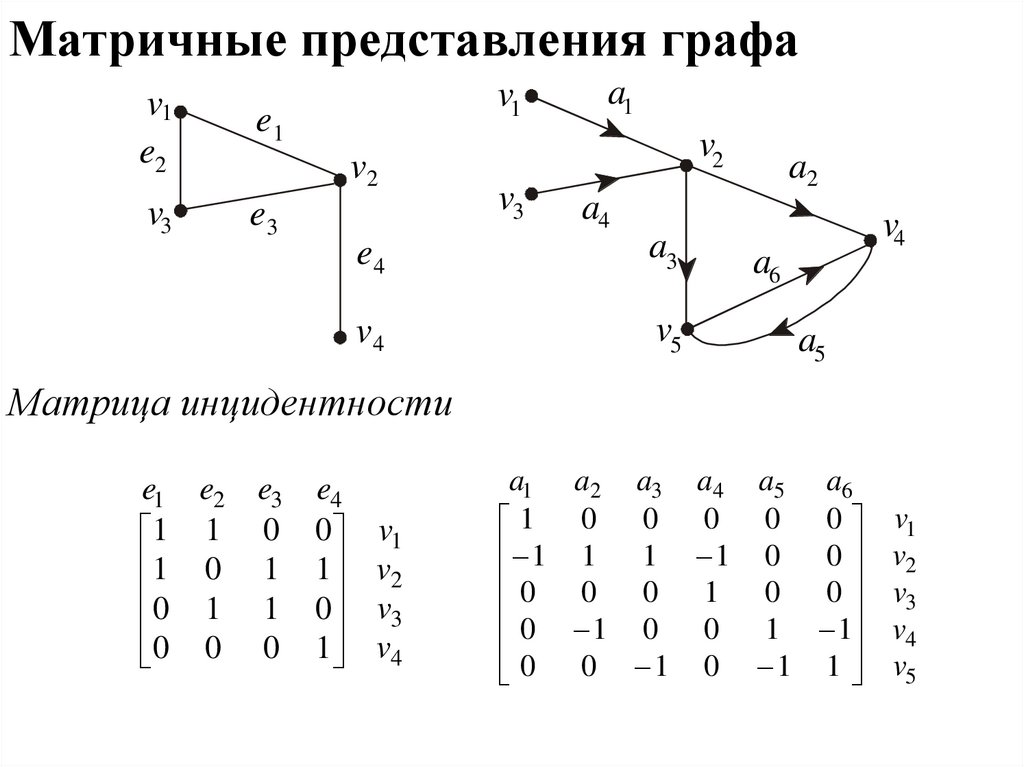
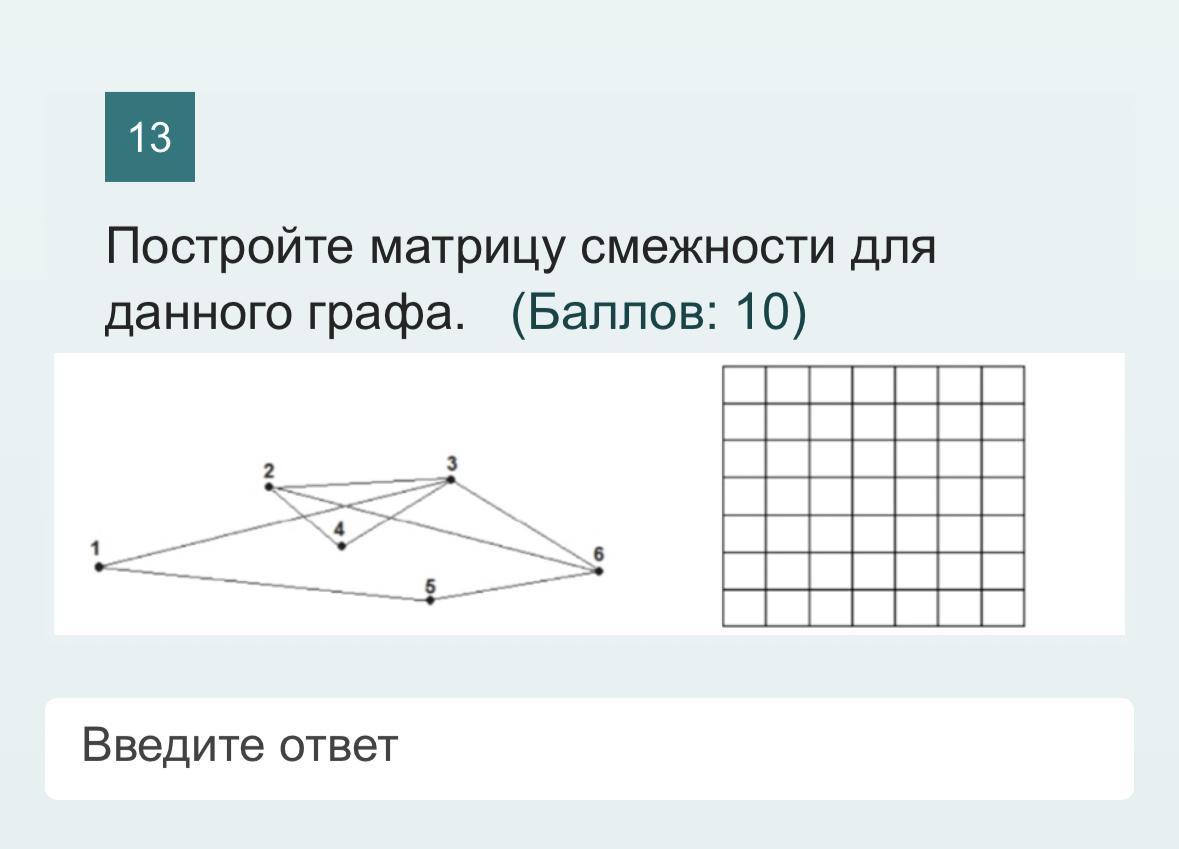
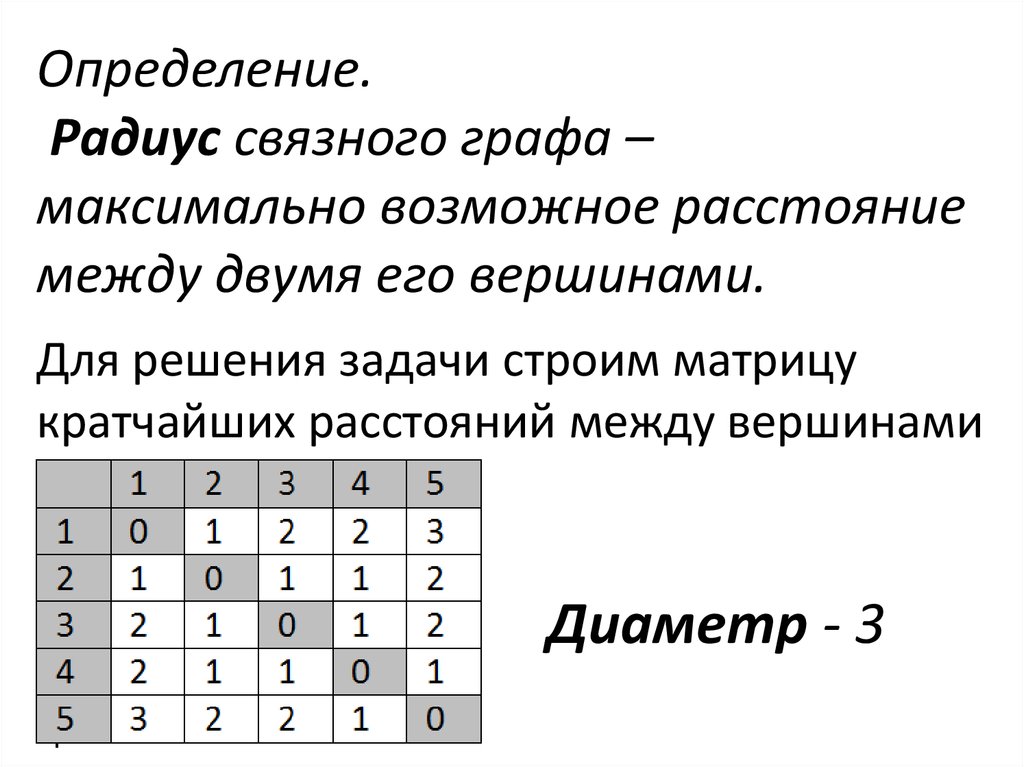
Радиус графа можно найти как минимальное расстояние от любой вершины до самой удаленной из других вершин.
Матрица смежности и расстояния. Расчёт топологических индексов Рандича и Винера
Если граф связан, то радиус можно определить как минимум из диаметров всех возможных подграфов.
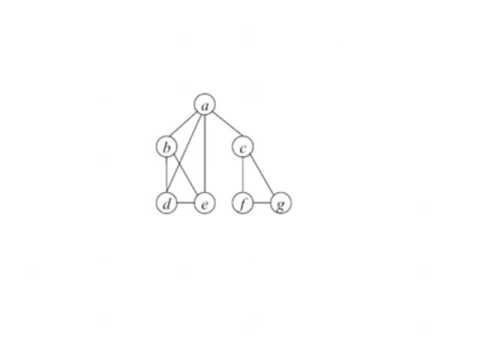
Обход графа в глубину
Не забывайте, что для ориентированных графов матрица смежности будет асимметричной, что повлияет на расчет радиуса.
Для больших графов используйте оптимизированные алгоритмы, такие как алгоритм Дейкстры для поиска кратчайших путей, чтобы ускорить расчеты.
8. Матрица расстояний
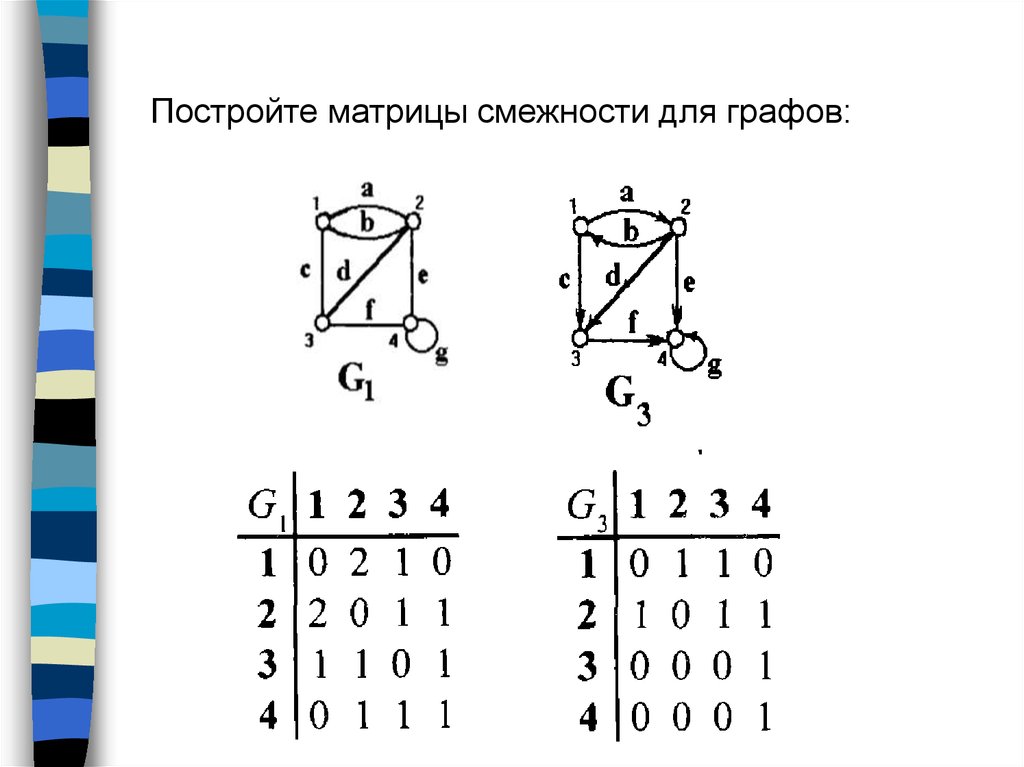
Рассматривайте связность графа перед расчетом радиуса — если граф не связан, радиус не существует.
Способы задать граф. Матрица векторов смежности

Информатика. Теория графов. Хранение графа: матрица смежности. Центр онлайн-обучения «Фоксфорд»
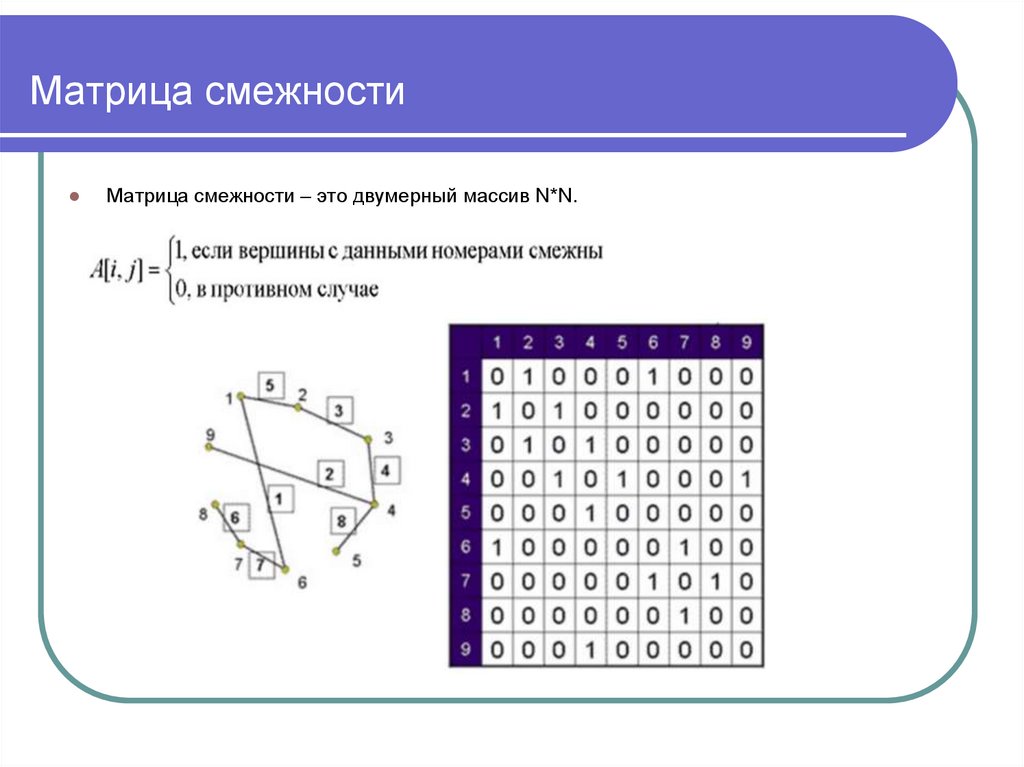
В некоторых случаях полезно использовать представление графа в виде списков смежности, чтобы сэкономить память и упростить вычисления.

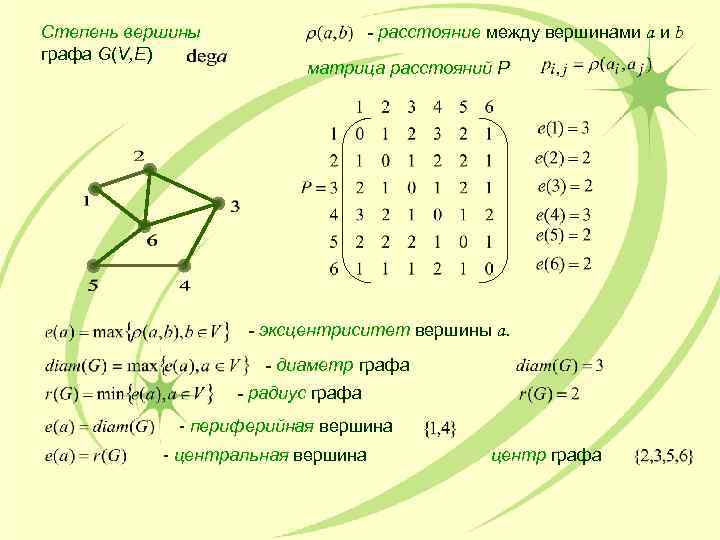
Диаметр графа. Радиус. Эксцентриситет. Центр
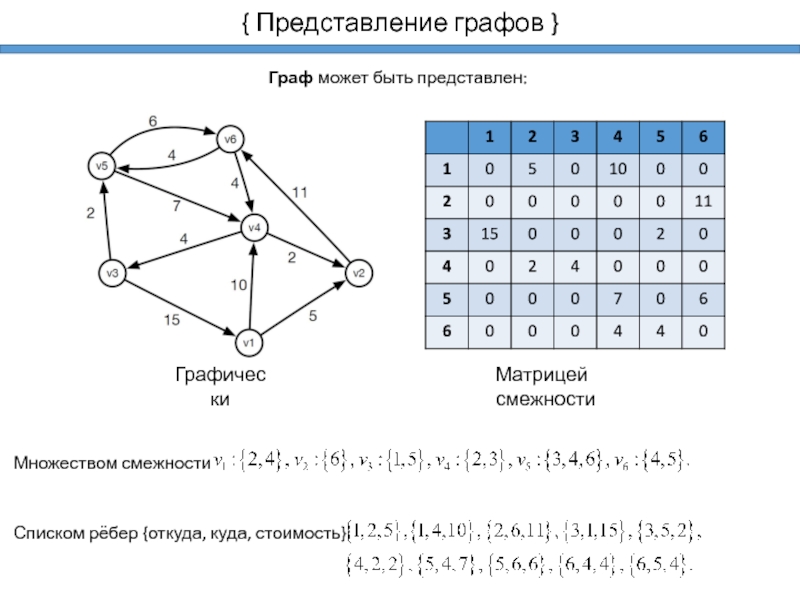
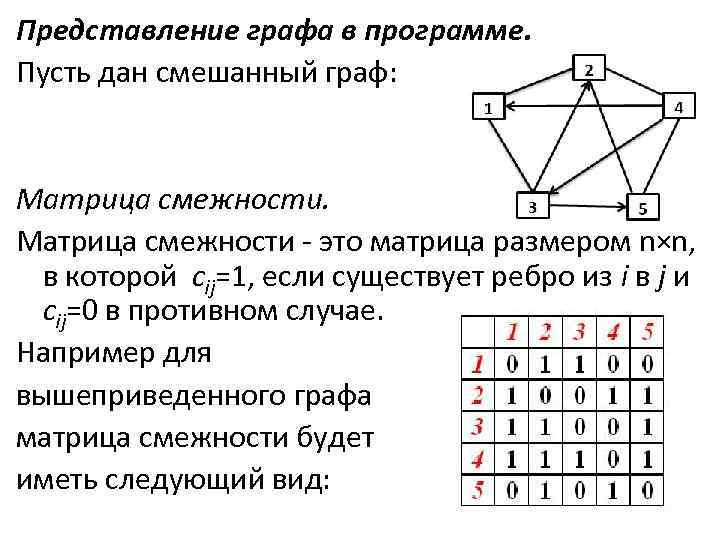
Проводите тесты на простых примерах графов, чтобы понять основные принципы работы с матрицами смежности и радиусом графа.

4.5 Расстояния в графах