Что такое подпространства линейных пространств и как их использовать в теории и практике?

Подпространство линейного пространства — это важная концепция в линейной алгебре, которая играет ключевую роль в различных математических и научных дисциплинах. Знание подпространств помогает глубже понять структуру линейных пространств и их применение в задачах анализа, геометрии и других областях.

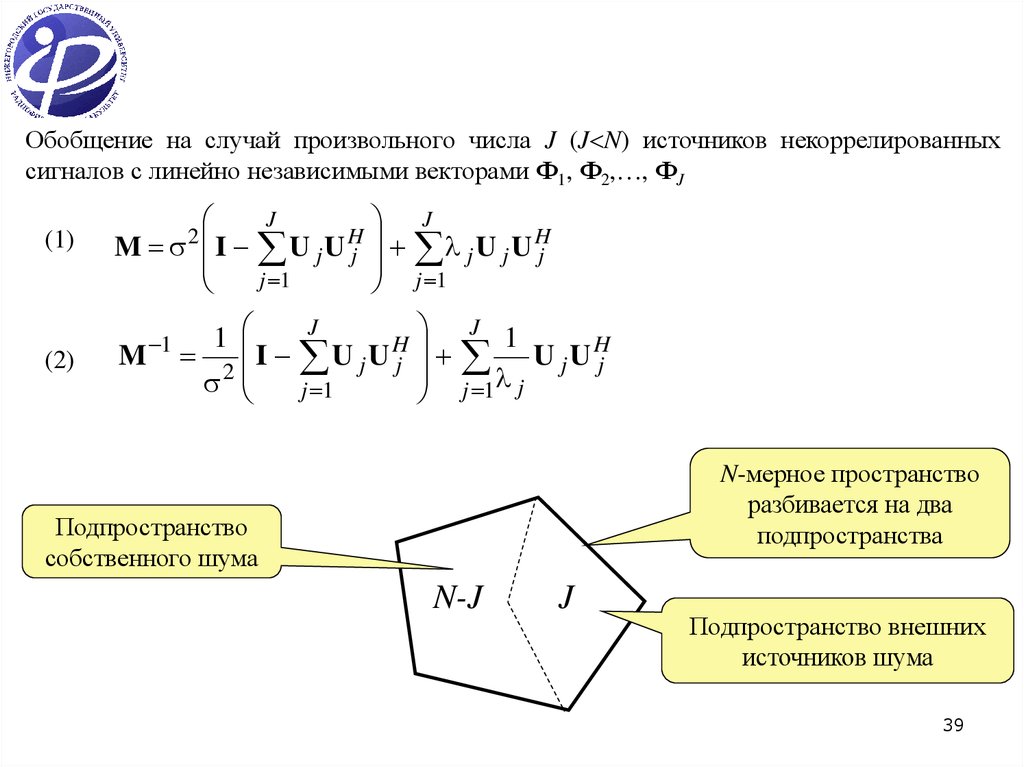
При изучении подпространств всегда проверяйте три основных условия: наличие нулевого вектора, замкнутость относительно сложения и умножения на скаляры.

Для того чтобы убедиться, что множество является подпространством, можно использовать теорему о критериях подпространства, проверяя, что оно удовлетворяет свойствам линейного пространства.

Не забывайте, что подпространства могут быть как конечномерными, так и бесконечномерными, что важно учитывать при решении задач на размерность.

Обратите внимание, что любое подпространство линейного пространства обязательно является линейным пространством само по себе, но не каждое множество является подпространством.

Изучая подпространства, полезно использовать методы матричных вычислений для нахождения базиса подпространства и его размерности.

Когда вы работаете с подпространствами, важно учитывать их геометрическую интерпретацию, например, линии и плоскости в пространстве могут служить примерами подпространств.

Если подпространство является решением системы линейных уравнений, можно найти его с помощью методов Гаусса или других алгоритмов для нахождения решения линейных систем.

Знание свойств подпространств линейных пространств критически важно при решении задач на проекции и разложения векторных пространств.

При изучении подпространств также полезно рассматривать вопросы независимости векторов и линейной зависимости в контексте подпространств.

Использование графического подхода может помочь вам наглядно увидеть, как подпространства взаимодействуют с другими элементами линейных пространств, особенно в двух- и трёхмерных случаях.