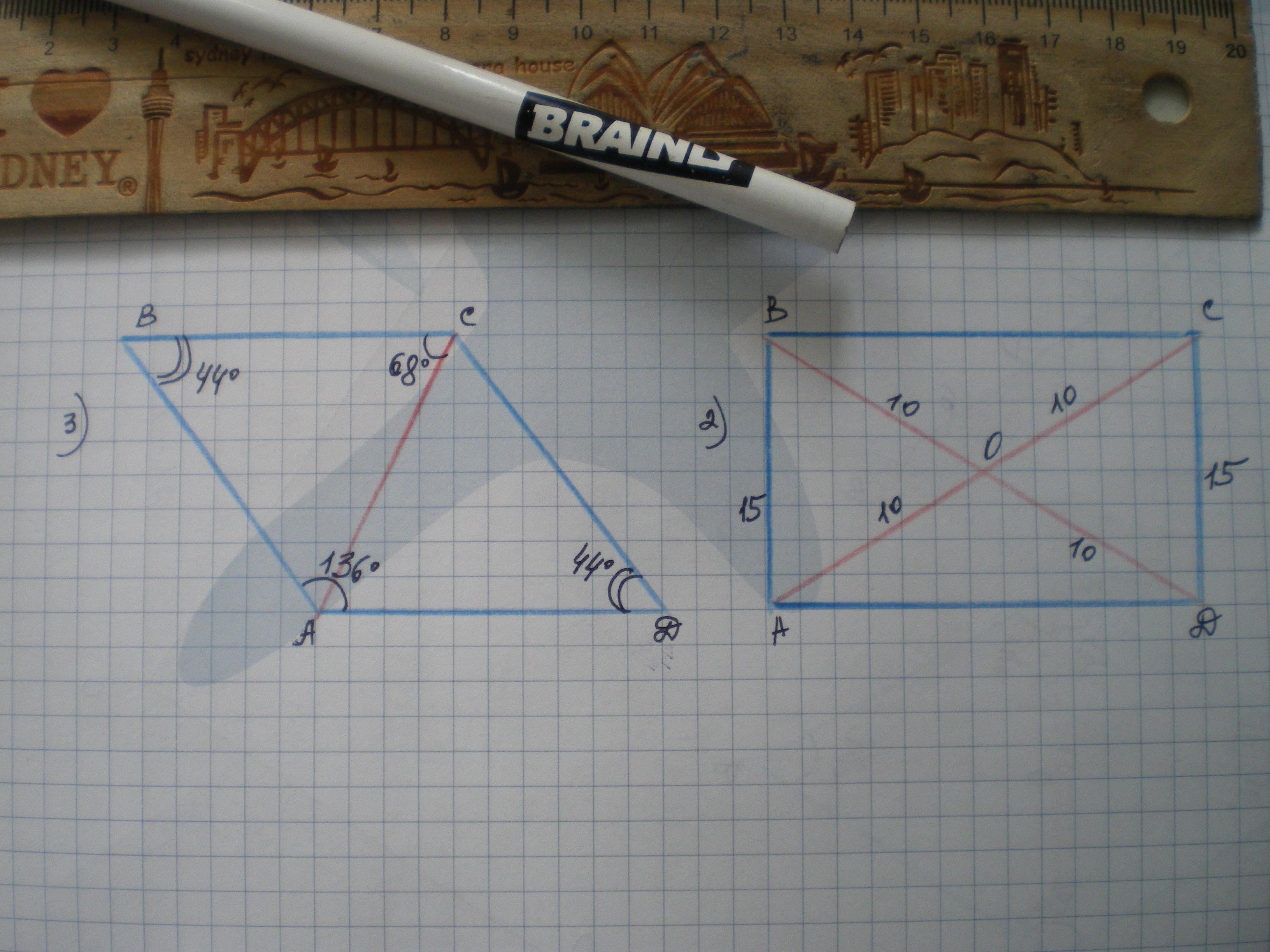
Все, что нужно знать о полупериметре параллелограмма и его вычислении
Полупериметр параллелограмма — это сумма длин всех его сторон, деленная на два. Этот параметр играет важную роль при расчете площади, периметра и других характеристик геометрических фигур. Чтобы научиться правильно вычислять полупериметр, важно понимать свойства параллелограмма и правильно применить соответствующие формулы.
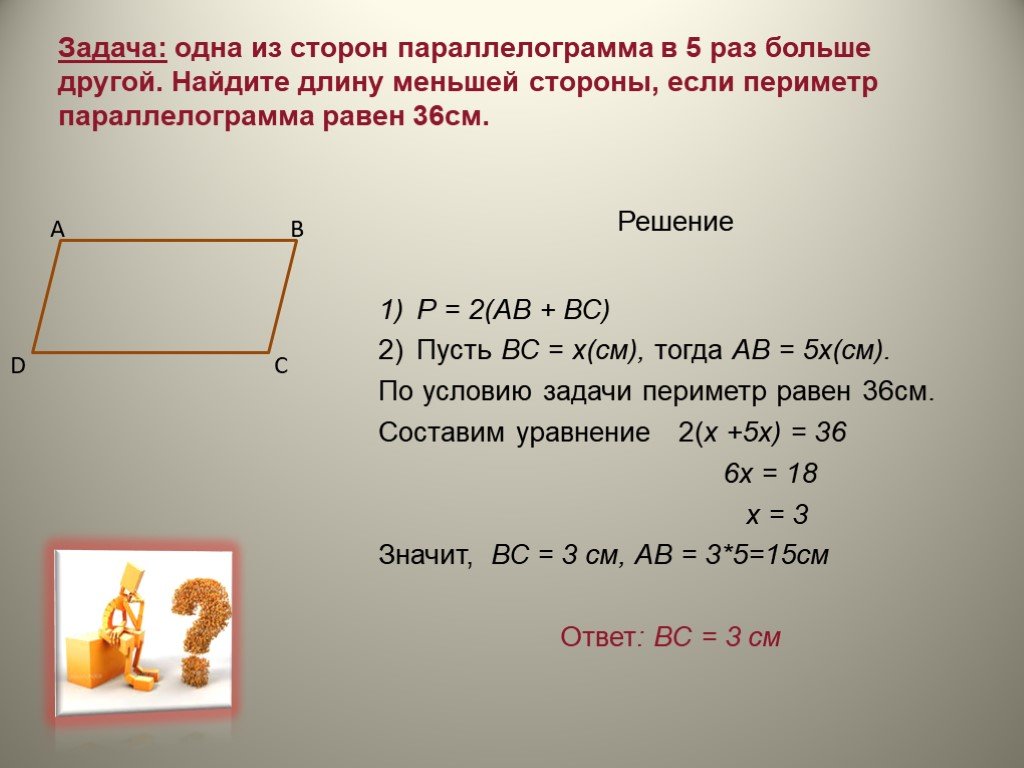
Для расчета полупериметра параллелограмма достаточно знать длины двух его сторон, так как противоположные стороны равны по длине.

Реакция на результаты ЕГЭ 2022 по русскому языку


Полупериметр параллелограмма можно найти, сложив длины всех его сторон и поделив на два. Формула: P = (a + b) * 2 / 2.
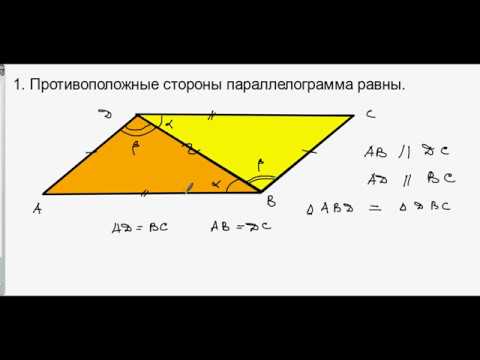
Свойства диагоналей параллелограмма.

При вычислении полупериметра важно учитывать, что противоположные стороны параллелограмма всегда равны.

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия
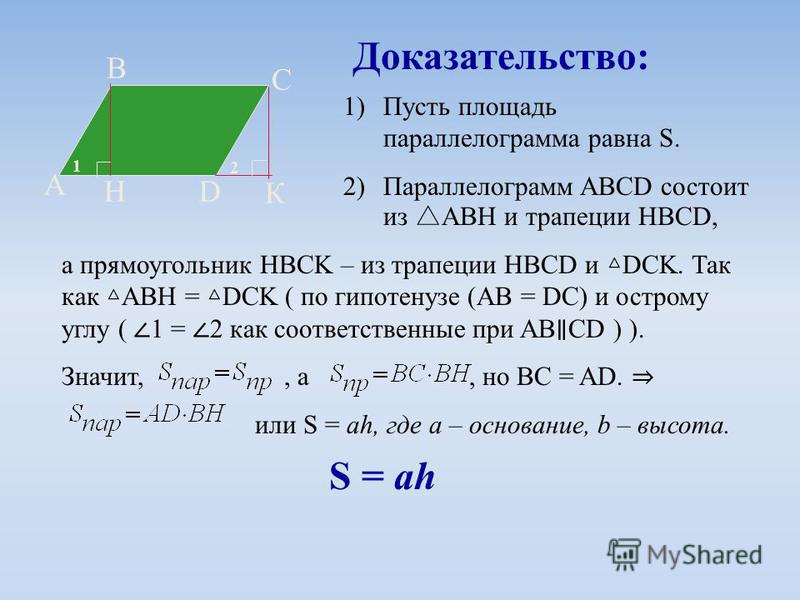
Понимание того, что полупериметр является половиной периметра, помогает упростить вычисления.

ЕГЭ 2017 - Задание 3 - Периметр параллелограмма равен ... ✘ Школа Пифагора
Если известны только углы параллелограмма, для нахождения полупериметра нужно сначала вычислить длины сторон, используя тригонометрические формулы.
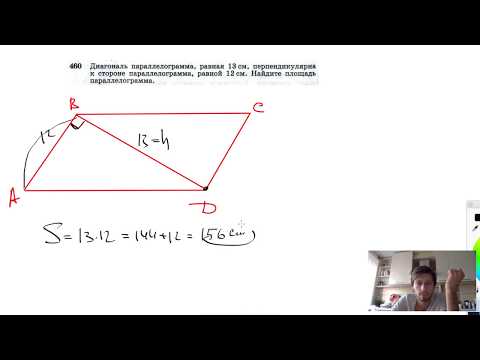
№460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма,
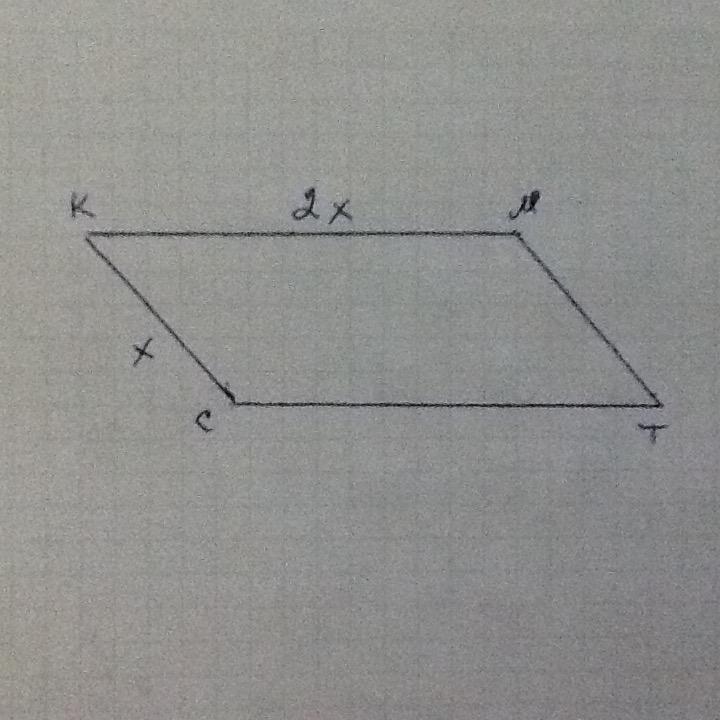
Помимо основного расчета полупериметра, полезно учитывать его связь с площадью параллелограмма, особенно при решении задач на нахождение площади.
Когда требуется найти площадь параллелограмма, можно использовать полупериметр в формулах, где он участвует в расчете высоты или других геометрических характеристик.
Если параллелограмм является ромбом, то все его стороны одинаковы, и для расчета полупериметра достаточно знать только одну сторону.
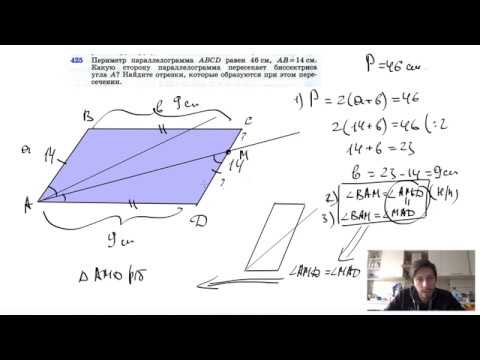
№425. Периметр параллелограмма ABCD равен 46 см, АВ=14см. Какую сторону параллелограмма

Периметр параллелограмма равен 112 см. Найдите его стороны, если одна из них на 12 см меньше другой.
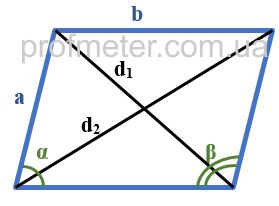
Для трапецеидального параллелограмма можно использовать аналогичные принципы, но необходимо помнить, что стороны могут быть разной длины.
Чтобы научиться лучше понимать геометрию параллелограммов, попробуйте решить несколько задач на вычисление полупериметра и площади, чтобы закрепить знание формул.

90°60°30° Как определить прямой угол?