Основы подграфов: ключевая роль в дискретной математике и теории графов

Подграфы — важная концепция в теории графов, являющаяся частью дискретной математики. Понимание подграфов помогает анализировать структуры и их связи в различных математических моделях и алгоритмах. В данной подборке вы найдете основные принципы и советы по работе с подграфами, а также примеры их использования в различных областях.

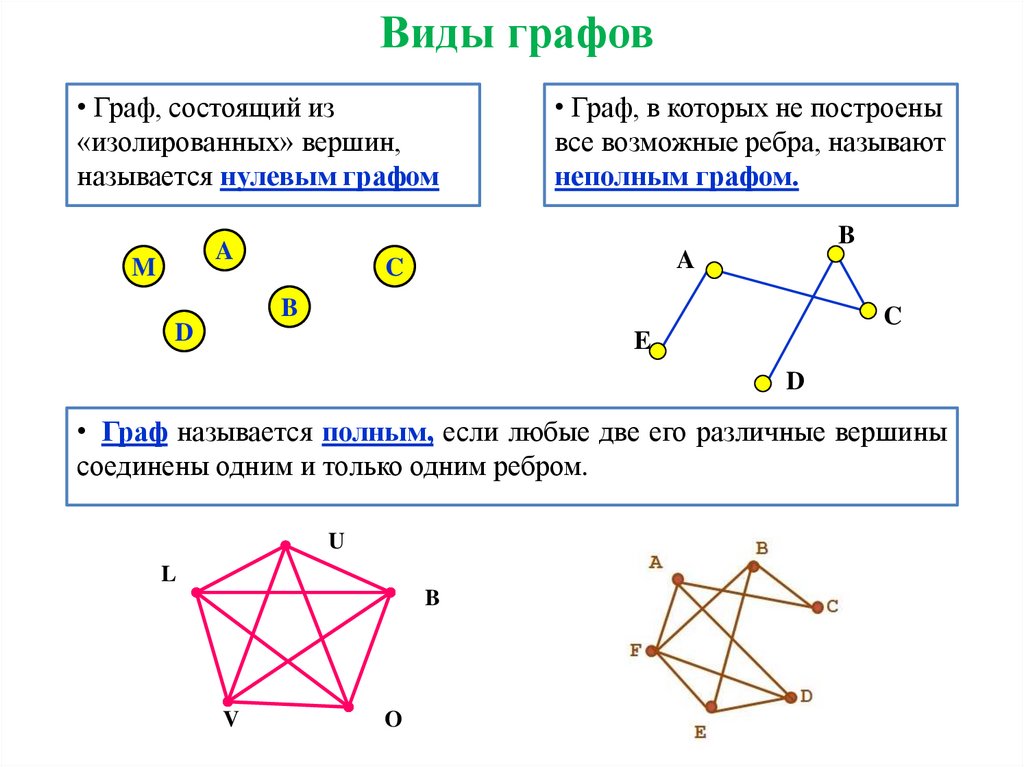
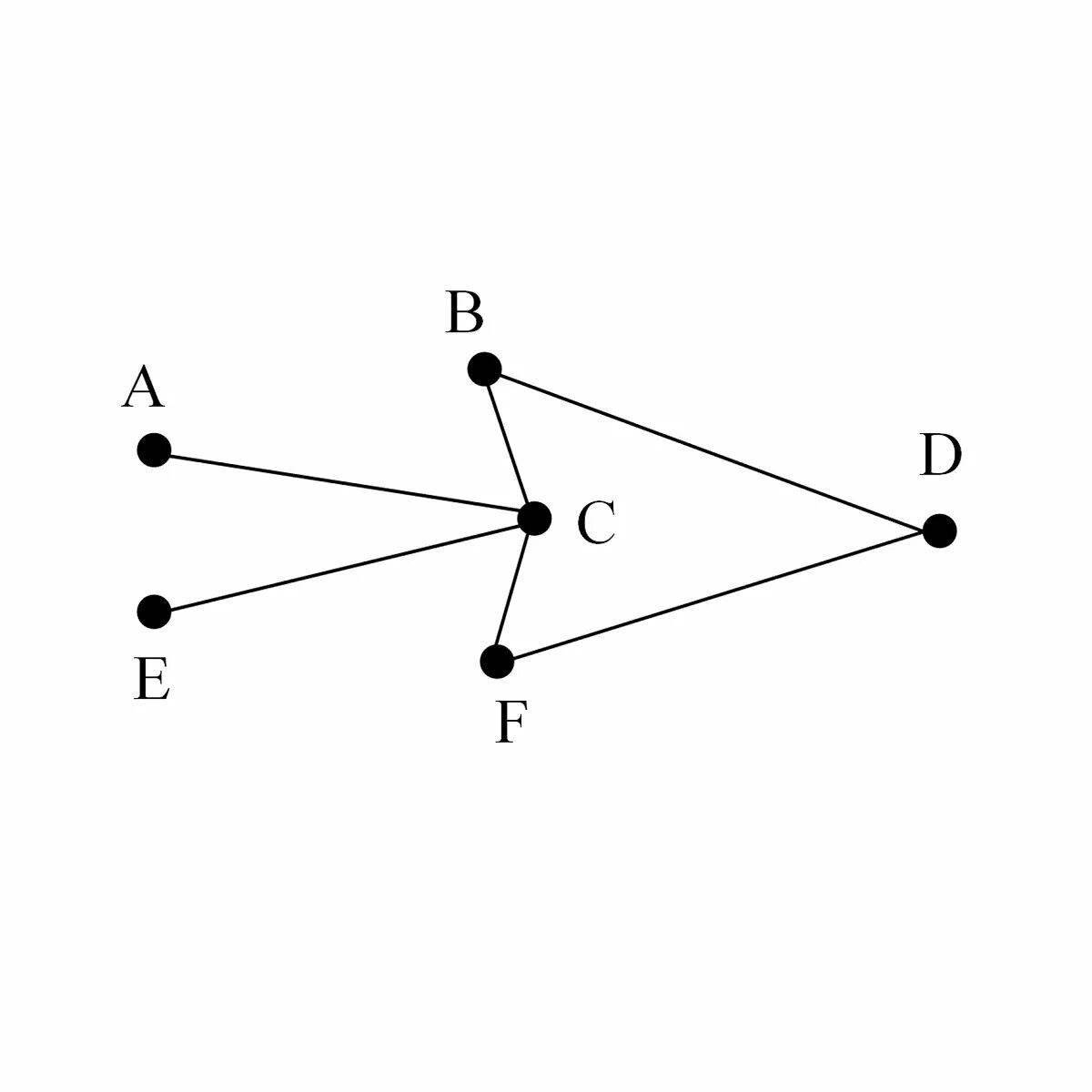
Подграф можно рассматривать как часть графа, включающую некоторое подмножество вершин и рёбер исходного графа.

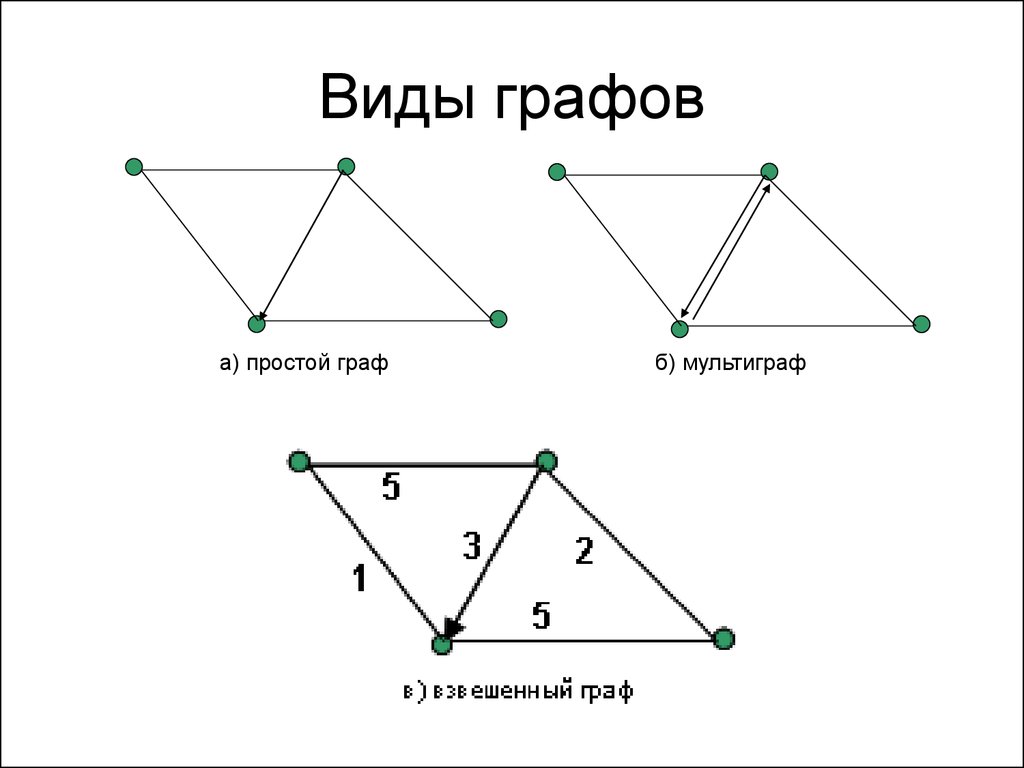
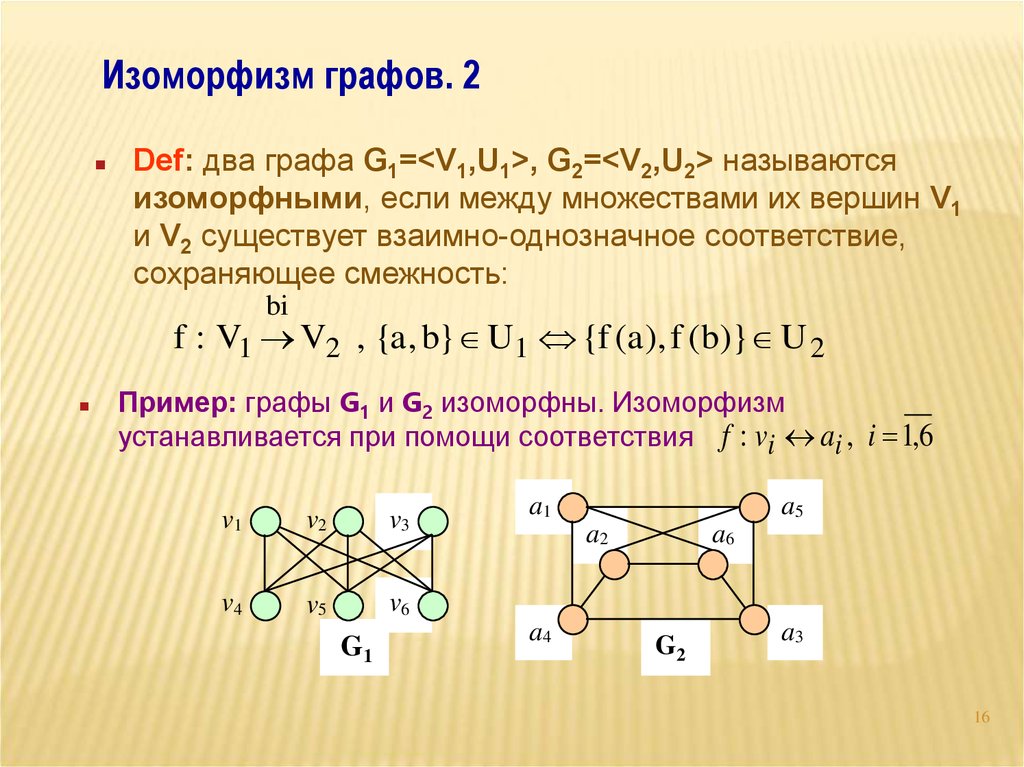
Для создания подграфа из графа важно правильно выбрать вершины и рёбра, которые будут включены в подграф.

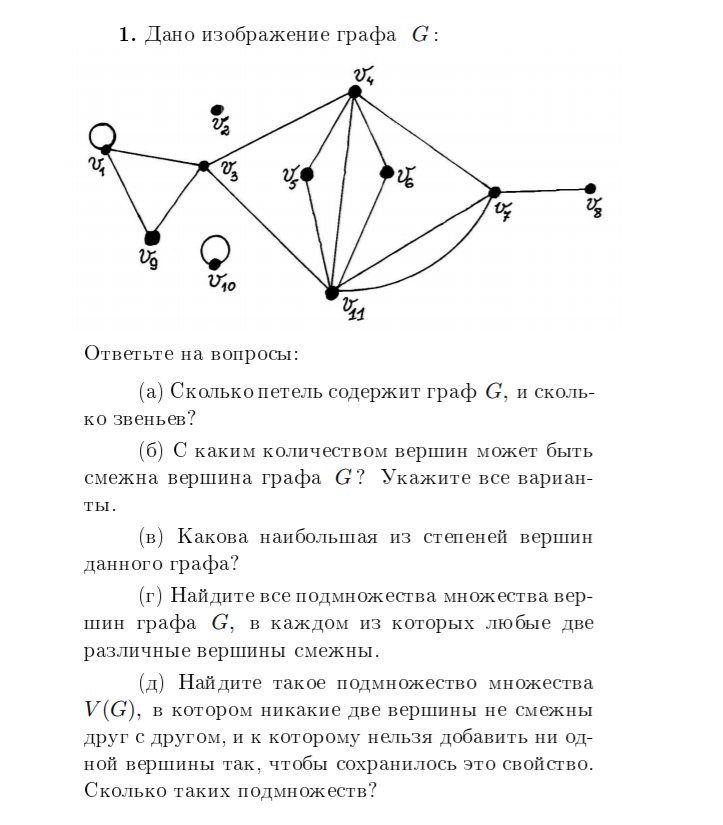
Если подграф включает все рёбра и вершины исходного графа, он называется индутированным.

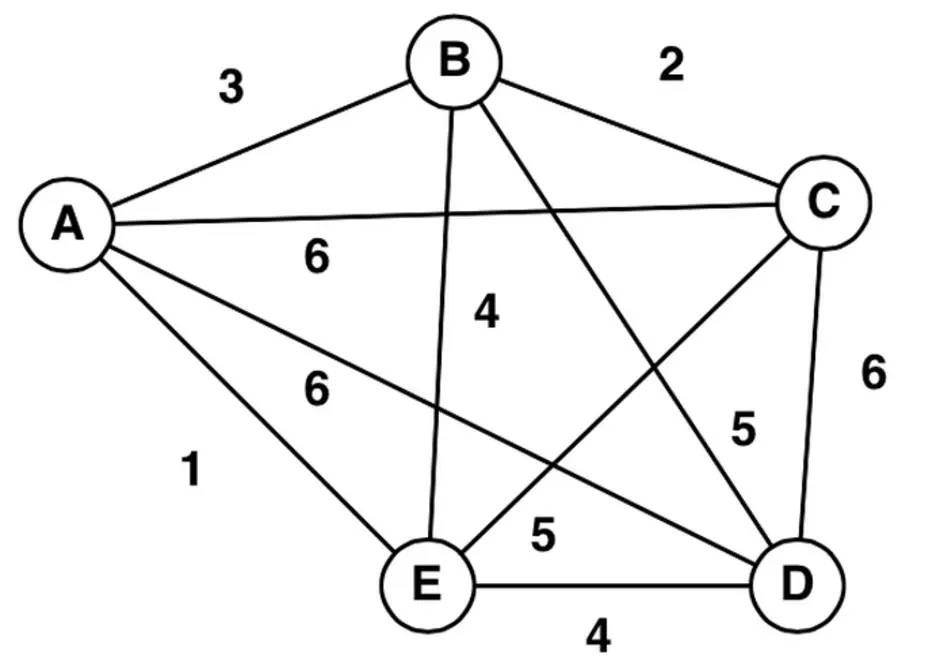
Подграфы могут использоваться для анализа связности графов и поиска кратчайших путей между вершинами.

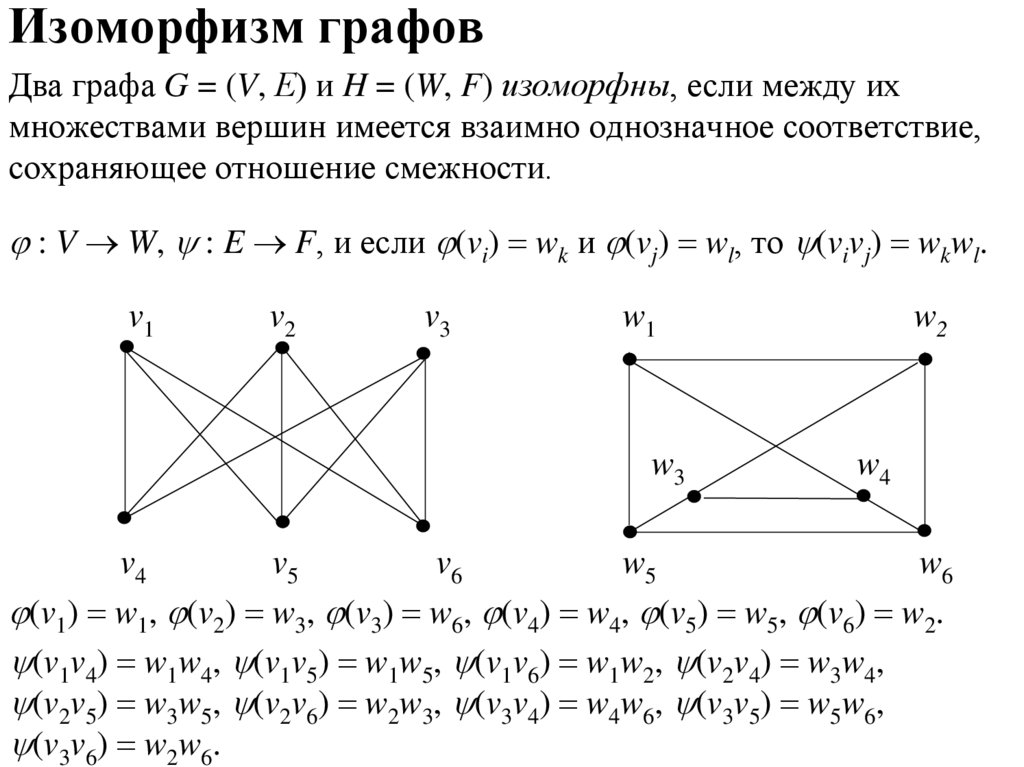
Чтобы узнать, является ли подграф компонентом связности, нужно проверить наличие путей между всеми вершинами подграфа.

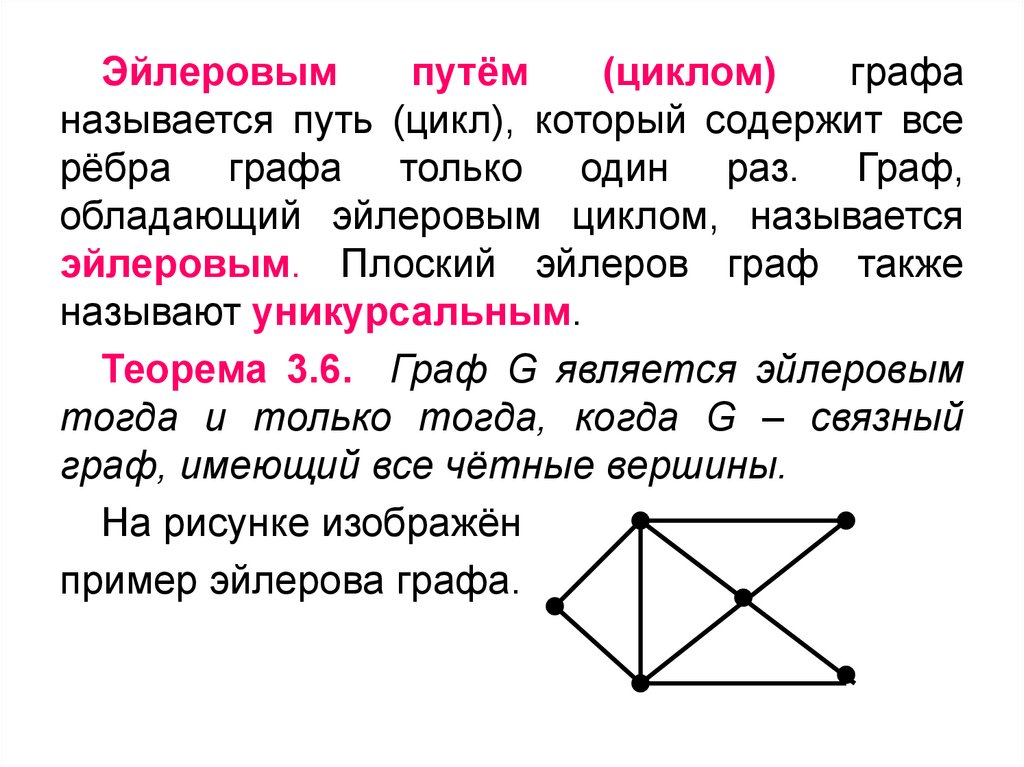
Иногда подграфы используются для решения задач о максимальных потока и остовных деревьях в графах.

Подграфы важны при анализе графов с точки зрения их структуры и локальных свойств.

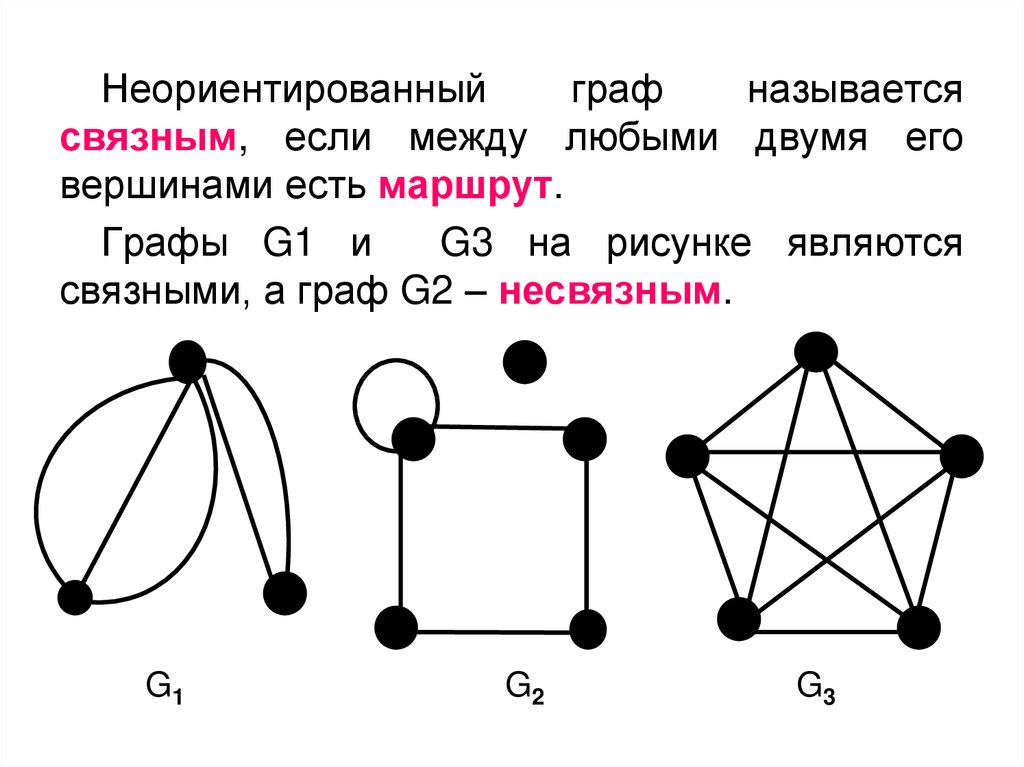
Подграфы играют ключевую роль в теоремах о графах, таких как теорема о планарности графа или теорема о четырёх красках.

Изучение подграфов помогает лучше понять, как различные элементы графа взаимодействуют друг с другом на более мелком уровне.

Для эффективной работы с подграфами полезно освоить алгоритмы поиска подграфов и их изоморфизмов в графах.