Как на основе графика функции выявить её основные характеристики
График функции — это наглядное представление зависимости между переменными, которое позволяет понять её поведение, характер изменений и ключевые свойства. Важно уметь правильно интерпретировать график, чтобы выделить такие характеристики, как экстремумы, точки пересечения с осями, монотонность и асимптоты. В этом разделе мы рассмотрим основные советы, как на основе графика функции описывать её свойства.
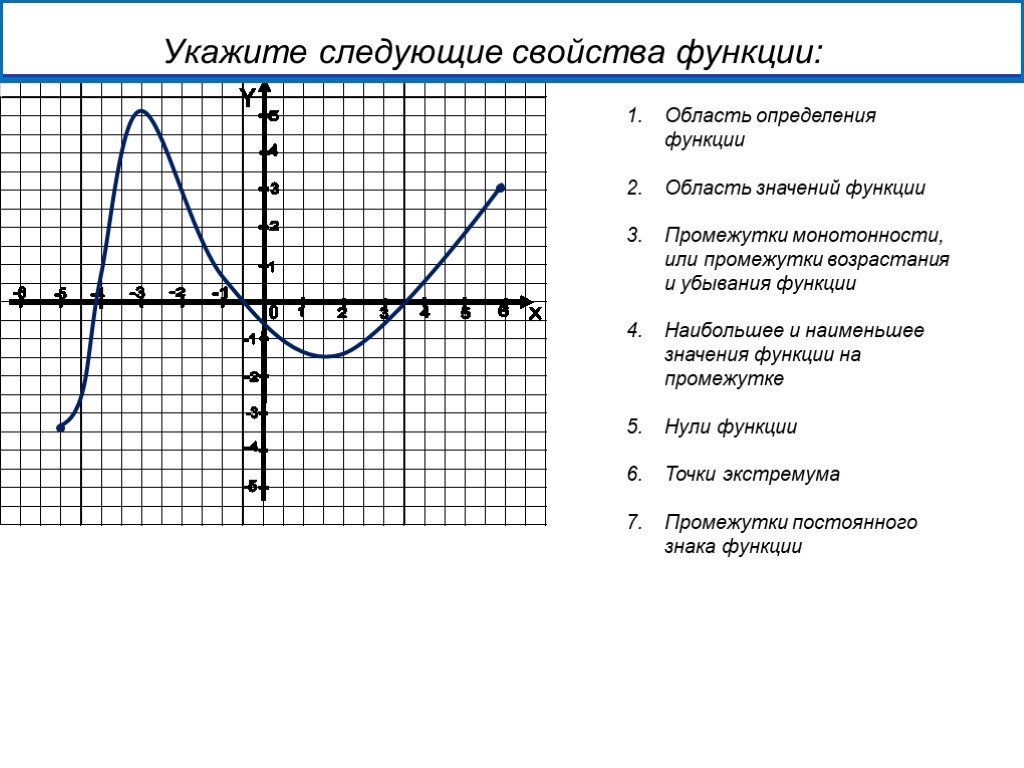

Начните с определения области определения функции, то есть интервала, на котором она задана.

Свойства функций. Алгебра, 9 класс

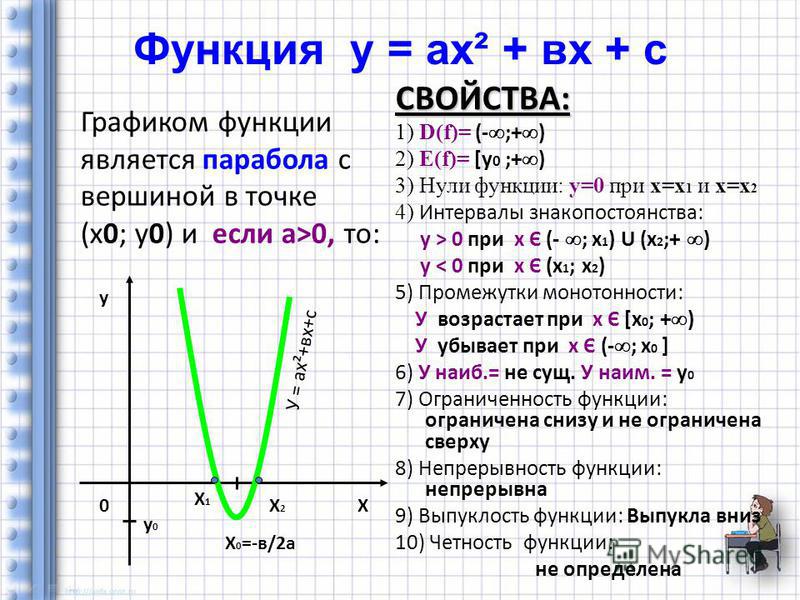
Определите вид графика: линейный, параболический, экспоненциальный или другой, чтобы сразу ориентироваться на характер изменений функции.

Чтение графиков функций. Определение свойств функции по графику.
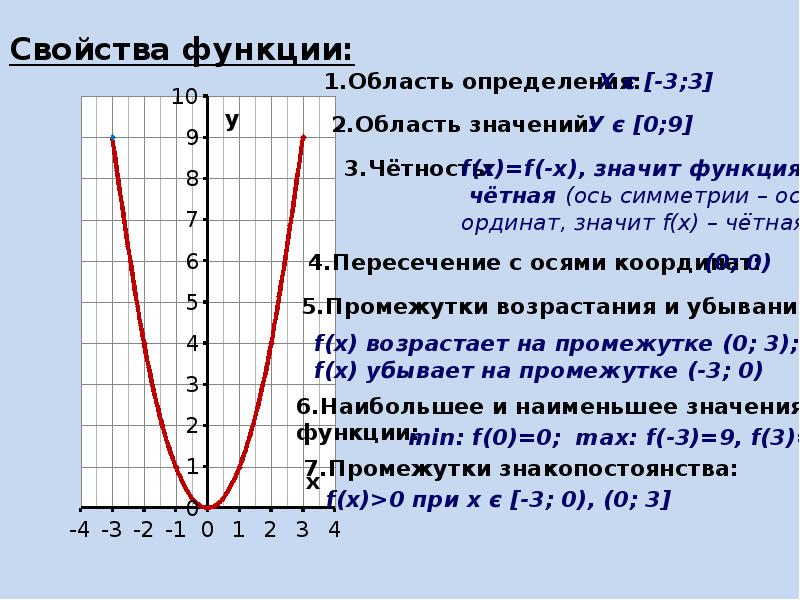

Обратите внимание на точки пересечения графика с осями: это может быть важно для понимания корней функции.
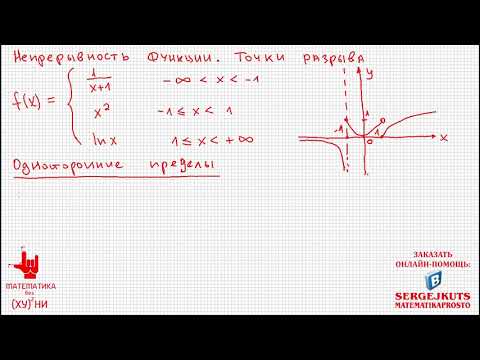
Математика без Ху%!ни. Непрерывность функции, точки разрыва.
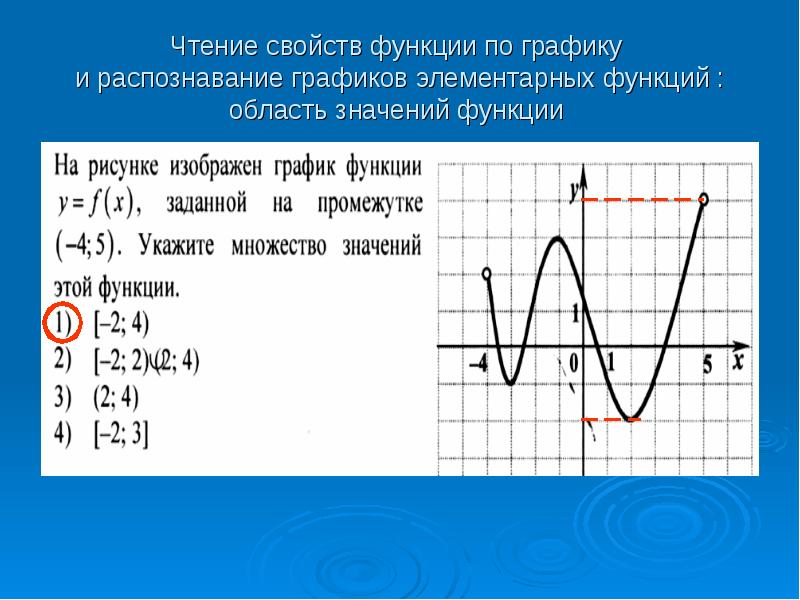
Ищите экстремумы (максимумы и минимумы) — они помогут определить поведение функции в разных точках.
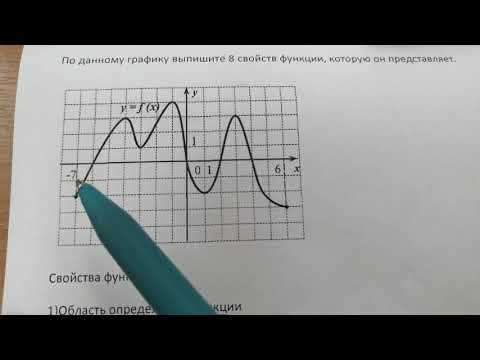
Чтение свойств функции по графику - 1
Оцените монотонность функции: возрастающая она или убывающая на каждом участке графика.

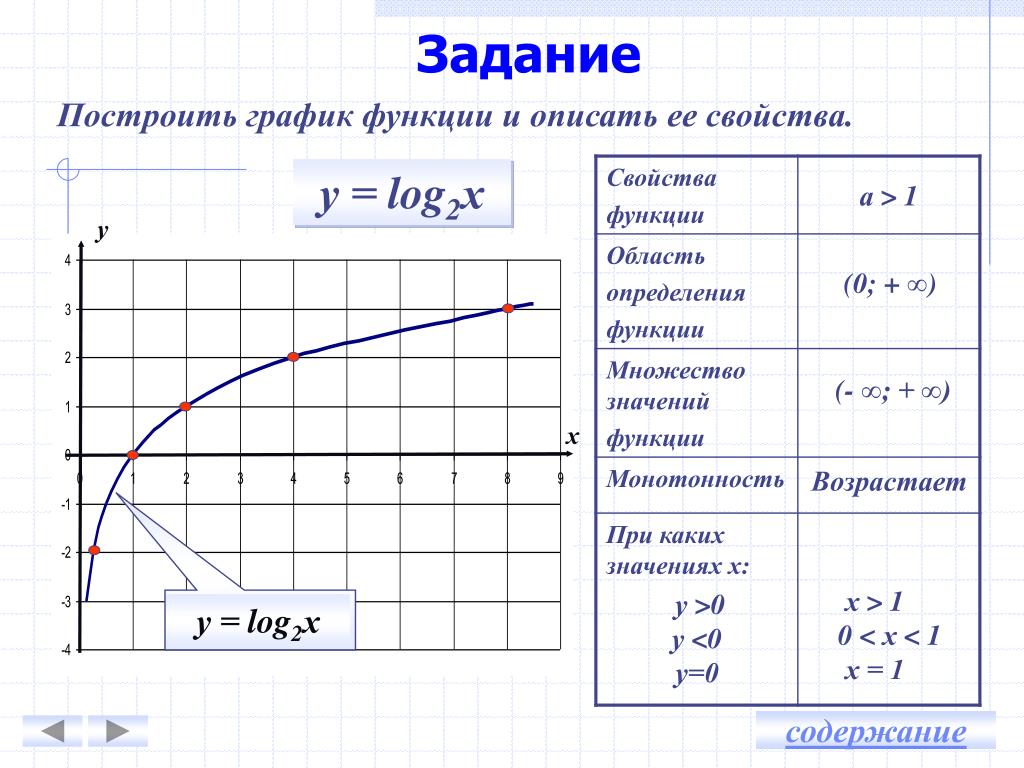
Проверьте, есть ли у функции асимптоты — горизонтальные, вертикальные или наклонные, это может многое рассказать о её поведении при стремлении переменных к бесконечности.

Для сложных графиков применяйте преобразования: смещение, растяжение, сжатие — это поможет более точно анализировать функцию.
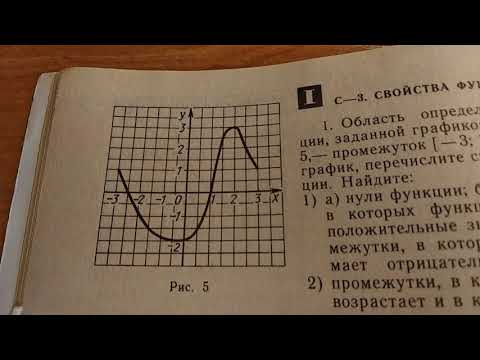
Свойства функции.

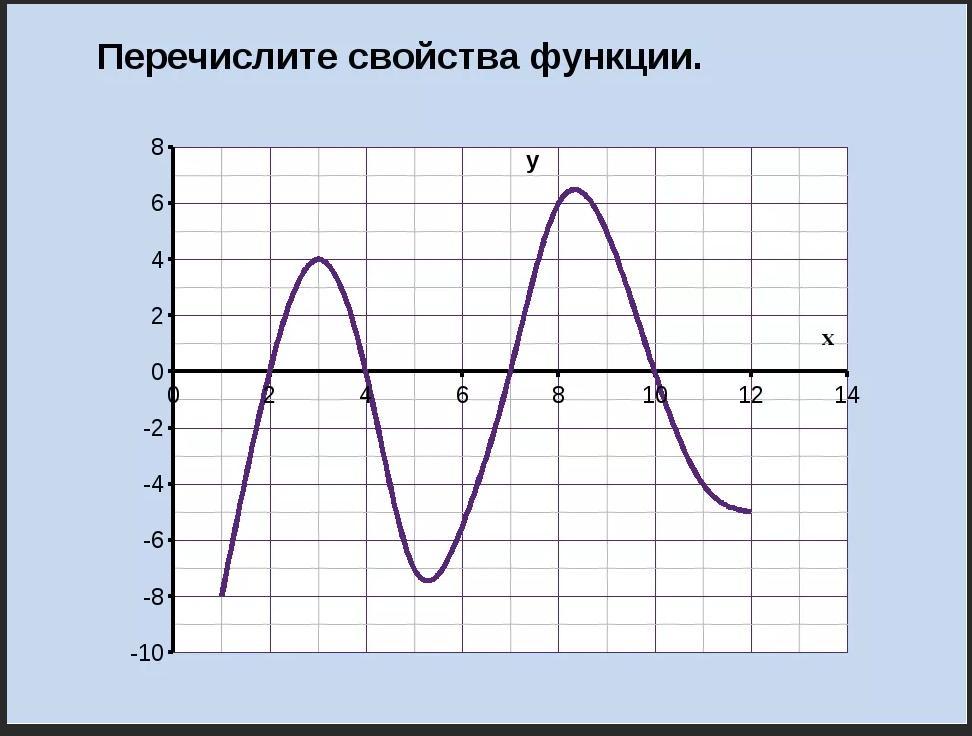
Не забывайте о периодичности функции, если график напоминает волну, это может свидетельствовать о том, что функция является периодической.
График функции y=sinx и ее свойства. 10 класс.

Алгебра ВСЕ Темы за 8 Класс / Математика с НУЛЯ за 30 МИНУТ / Маркова
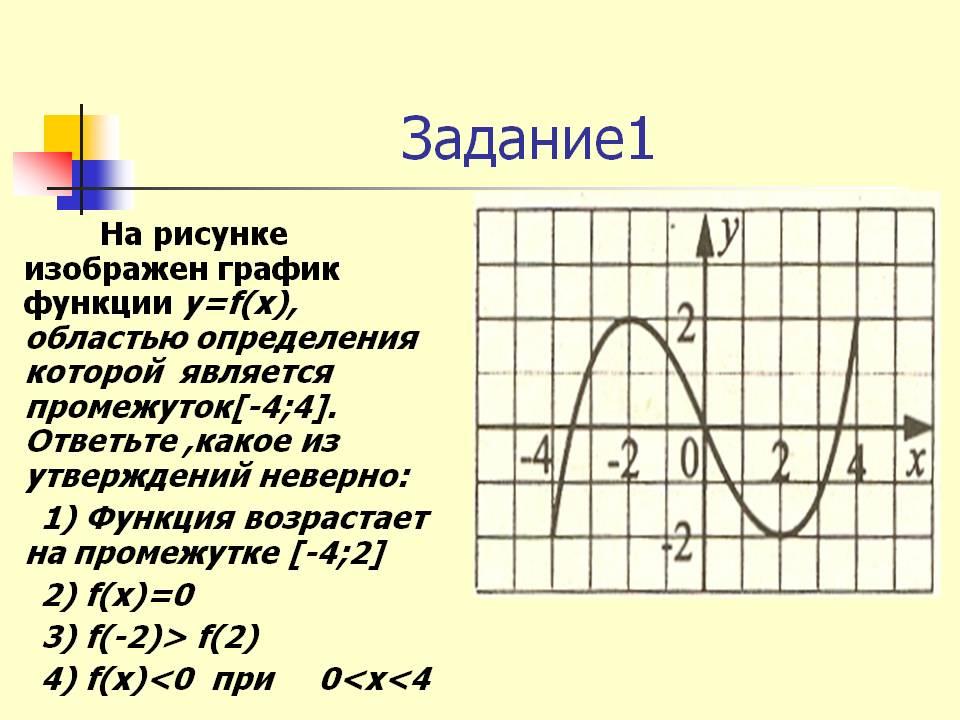
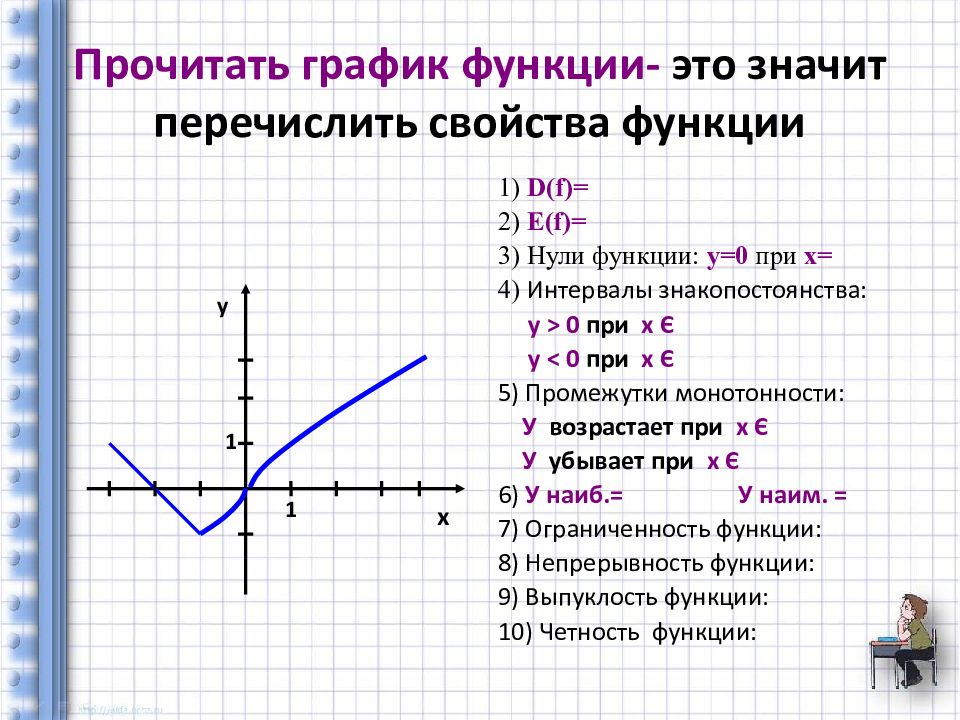
Обратите внимание на асимптотическое поведение функции — важно понимать, как она ведет себя при стремлении к бесконечности или нулю.
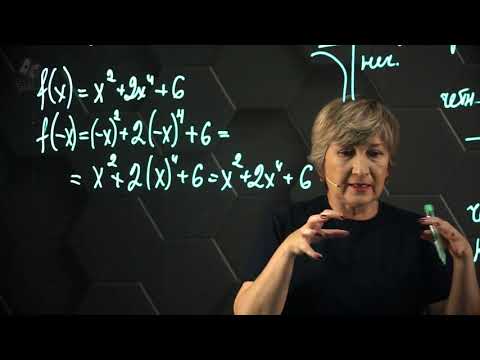
Свойства функции. Четность и нечетность функции. 10 класс.
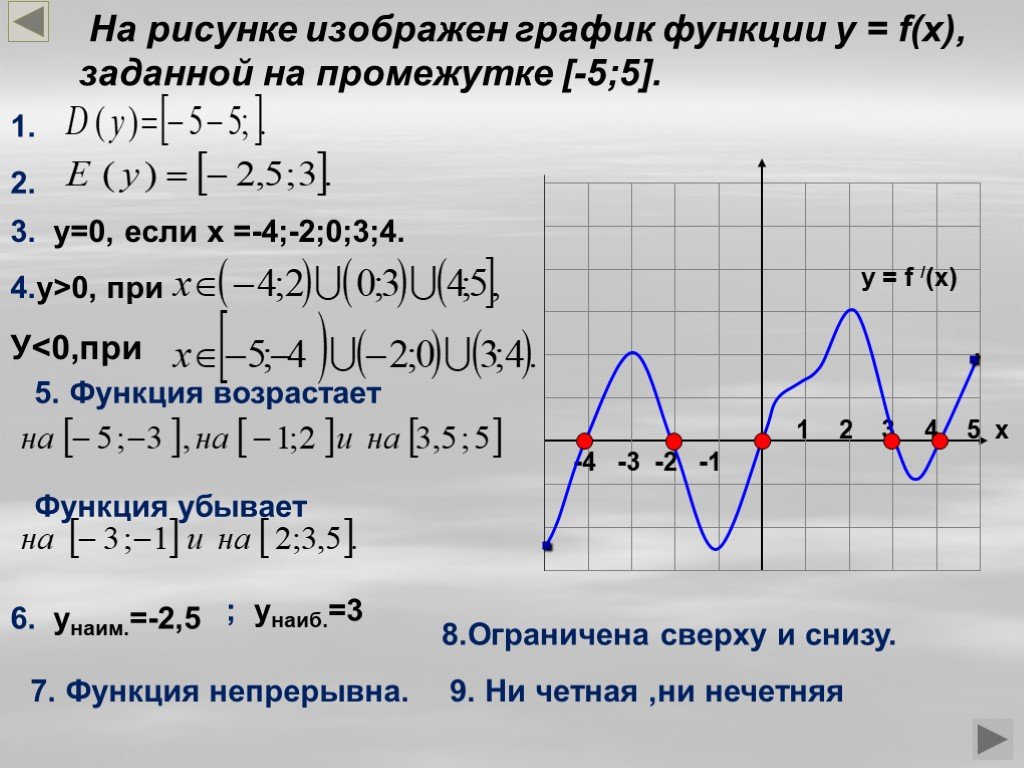
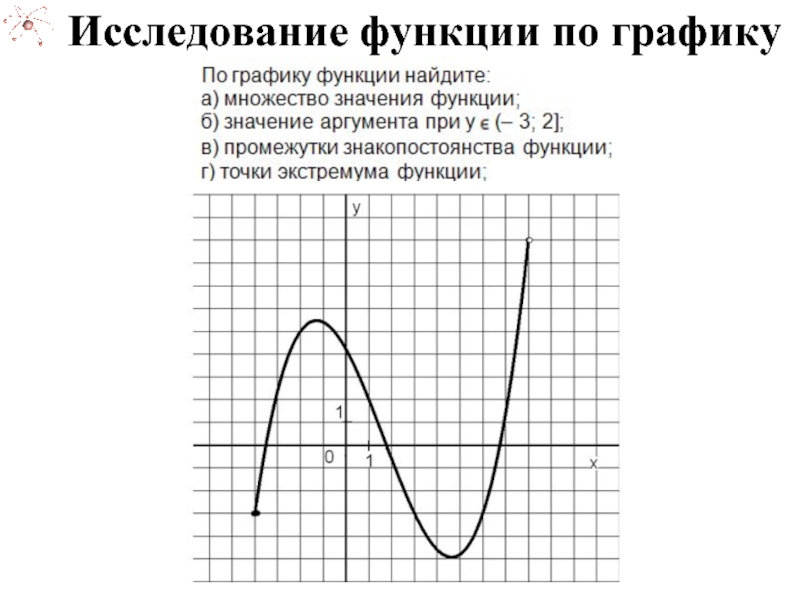
Не забывайте о симметрии графика: функция может быть четной или нечетной, и это определяет её поведение относительно оси y или x.

СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули Функции
