Методы нахождения площади заштрихованной области через интегралы: советы и примеры
На этой странице вы найдете подробное руководство по вычислению площади заштрихованных фигур с помощью интегралов. Мы рассмотрим основные методы, подходы, а также дадим полезные советы, которые помогут вам легче понять и решить задачи, связанные с нахождением площади через интегралы. Эти знания будут полезны не только для студентов, но и для всех, кто изучает математический анализ и геометрию.


Для начала определите границы фигуры и функции, которые ограничивают ее.

Применение определенного интеграла. Площадь криволинейной фигуры.

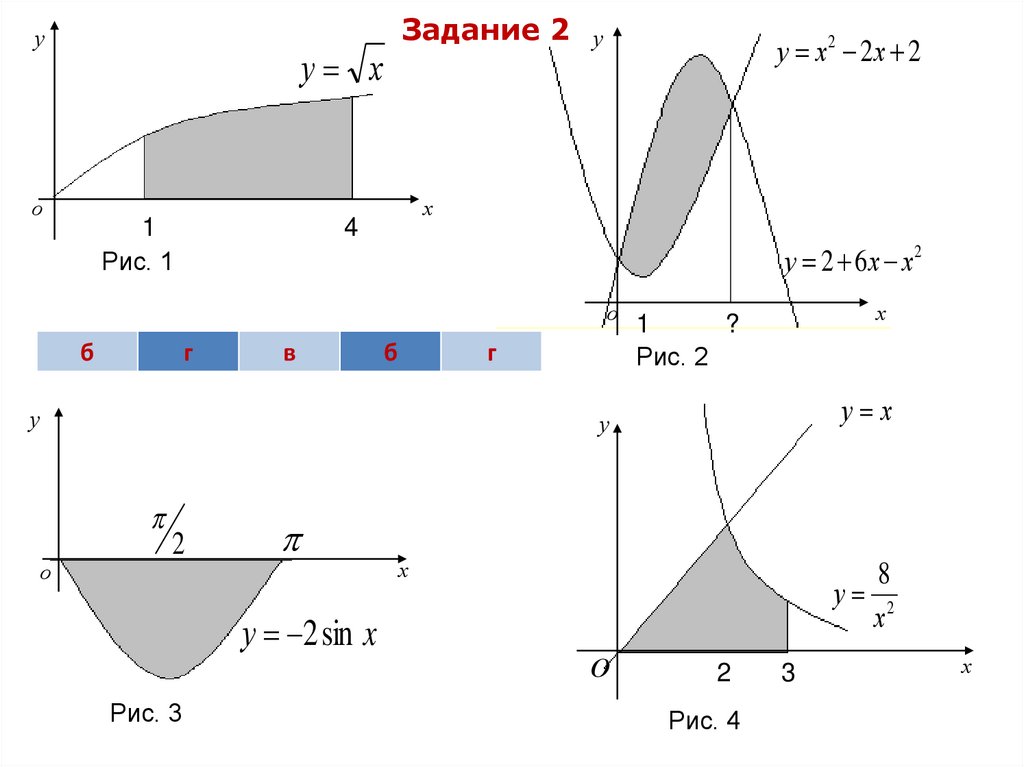
Важно понимать, какие области заштрихованы, чтобы правильно выбрать пределы интегрирования.

Вычисление площадей определённым интегралом
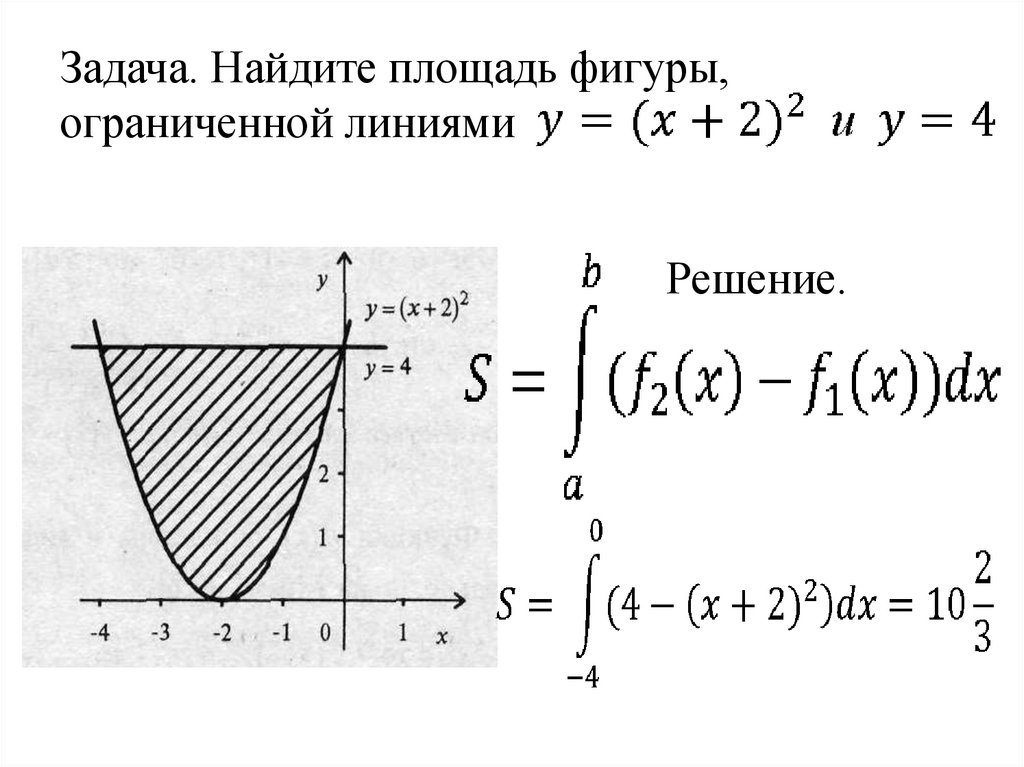
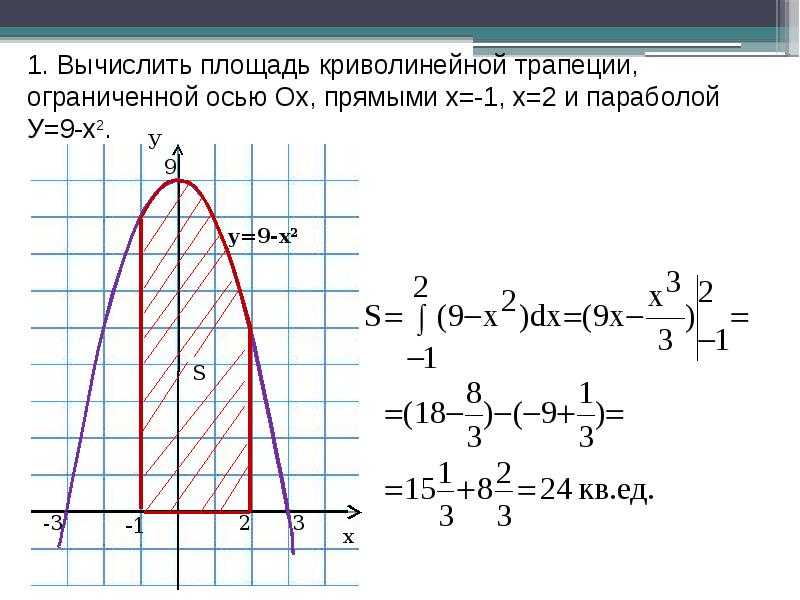
Не забывайте проверять, является ли функция, ограничивающая фигуру, непрерывной на данном интервале.
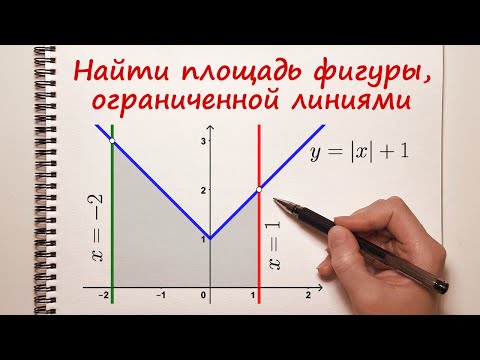
Найти площадь фигуры, ограниченной линиями. Пример 2.
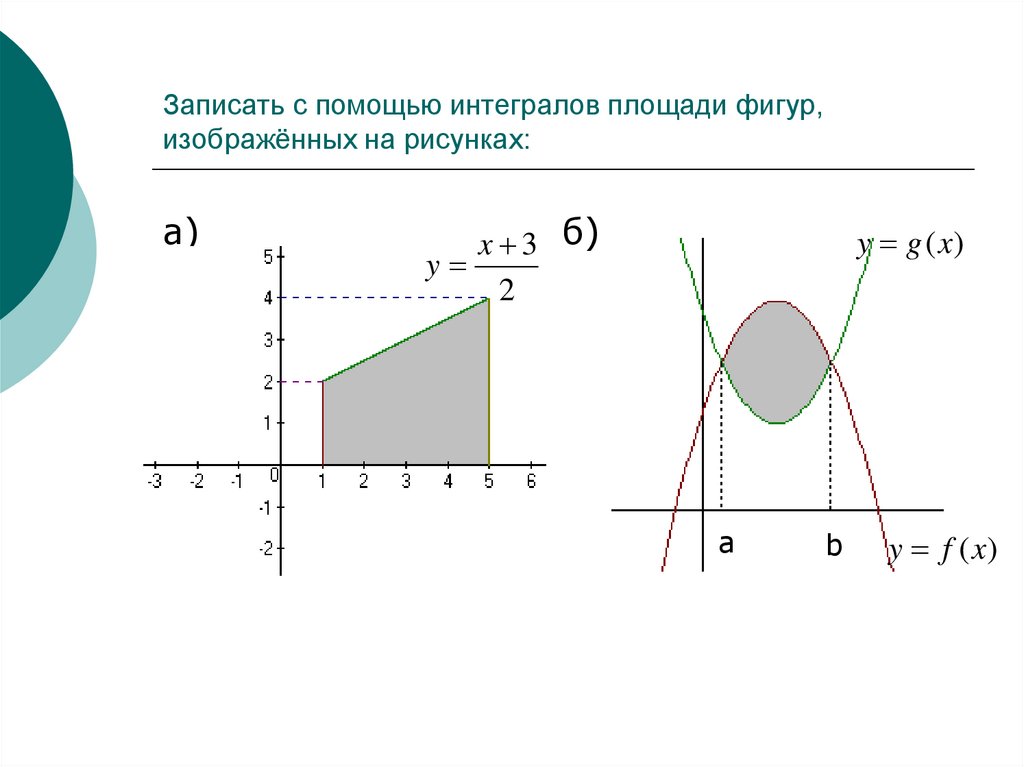

Использование вертикальных или горизонтальных прямых для определения границ области может значительно упростить решение.
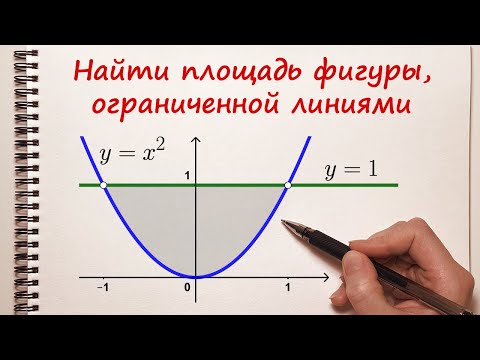
Найти площадь фигуры, ограниченной линиями. Пример 1.

В некоторых случаях можно воспользоваться симметрией фигуры, чтобы упростить вычисления.

Площадь фигуры через интеграл
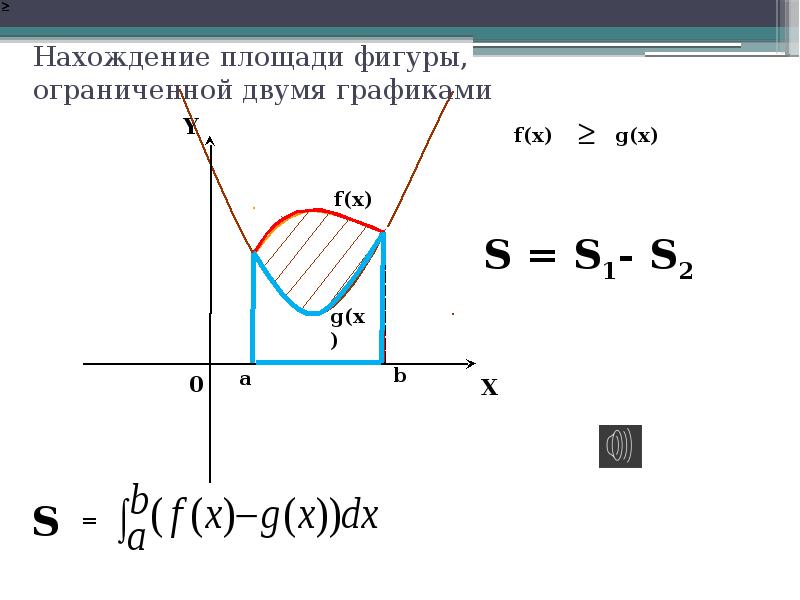
Если фигура состоит из нескольких областей, разбейте задачу на несколько интегралов и решите их поочередно.
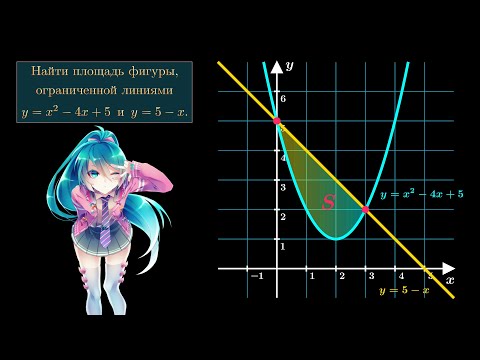
Интеграл для расчёта площади

Обратите внимание на тип интеграла: для нахождения площади часто используется определенный интеграл.
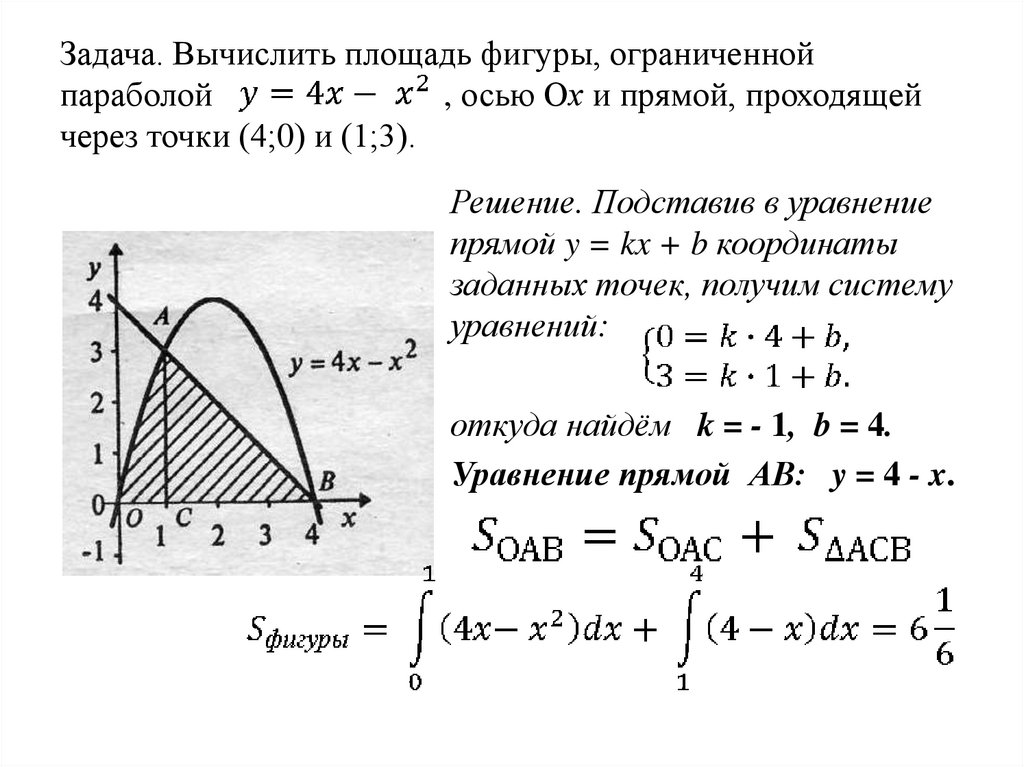
Используйте графическое представление для лучшего понимания расположения границ области и заштрихованных участков.
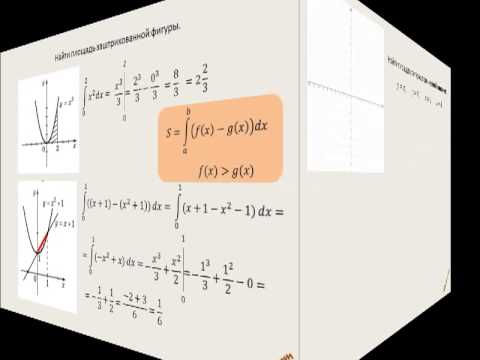
Интеграл для нахождения площади фигуры ч1
Проверьте свои вычисления, чтобы избежать ошибок при нахождении площади.
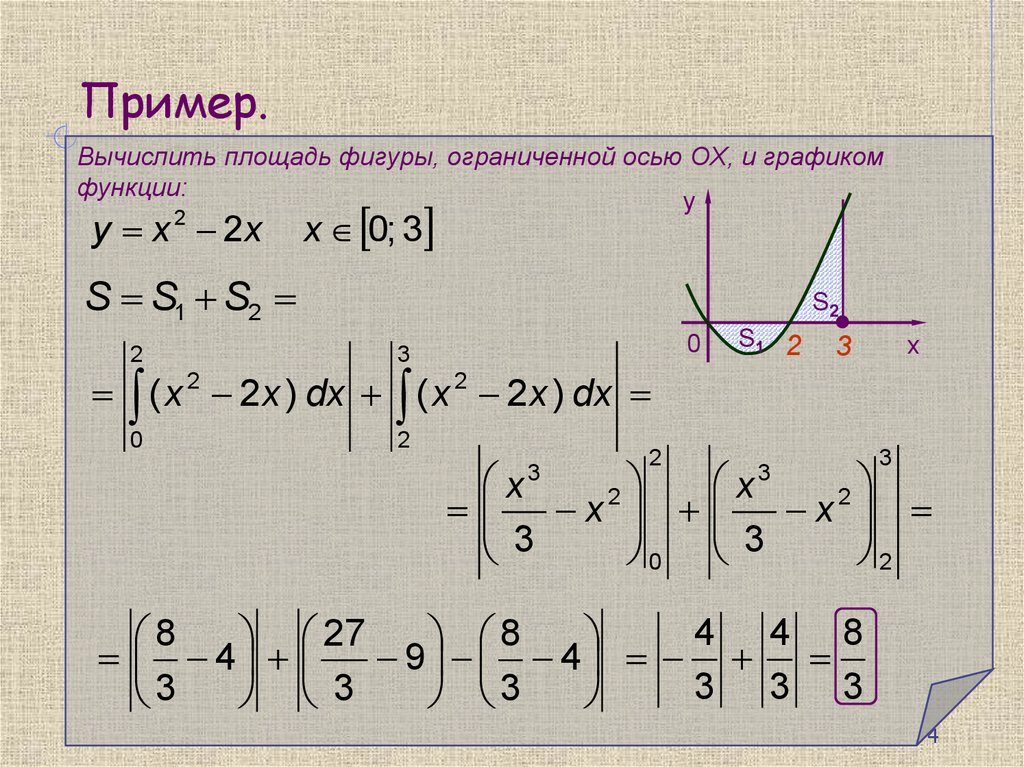
Если задача имеет сложную форму, рассмотрите возможность применения численных методов для вычисления площади.
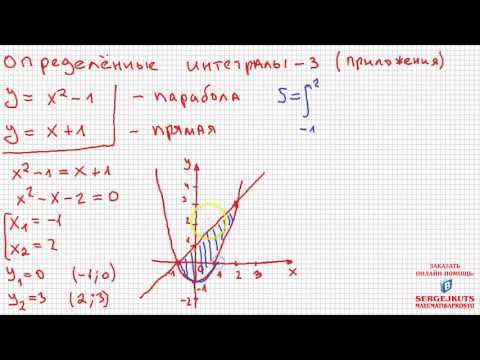
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.
