Как эффективно решать задачи на пересечение графов: важные советы и подходы
Пересечение графов — это важная тема в теории графов, изучающая пересечения рёбер и вершин различных графов. В этой статье собраны полезные советы и методы, которые помогут вам лучше понять и решать задачи, связанные с пересечением графов, а также применить эти знания на практике.
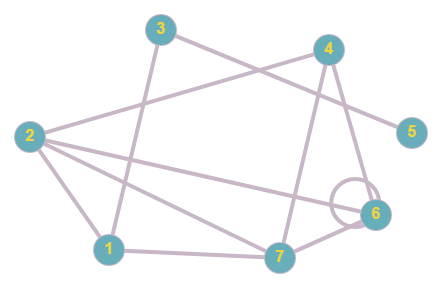

Для успешного решения задач на пересечение графов важно начать с анализа структуры графов, которые будут пересекаться, и выделить ключевые рёбра и вершины.

Операции над графами
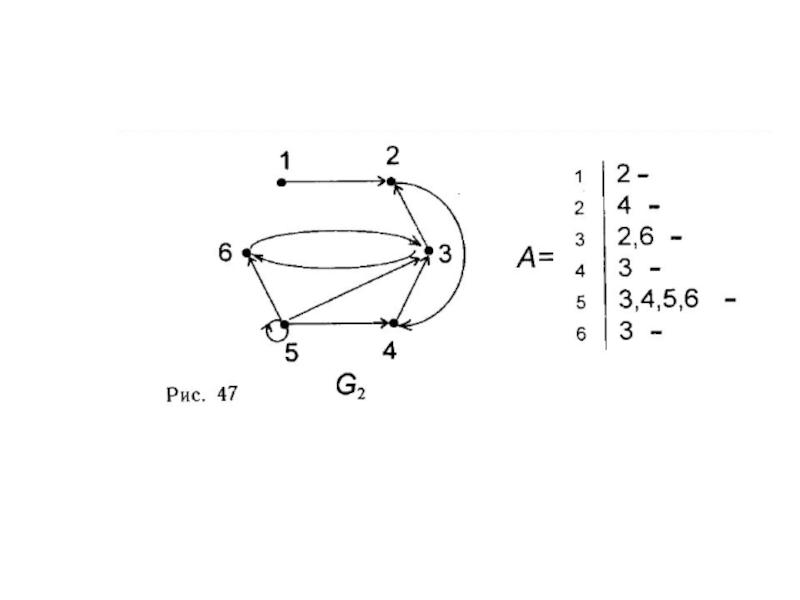

Использование алгоритмов поиска в глубину или ширину помогает выявить возможные пути пересечения рёбер и оптимизировать решение задачи.
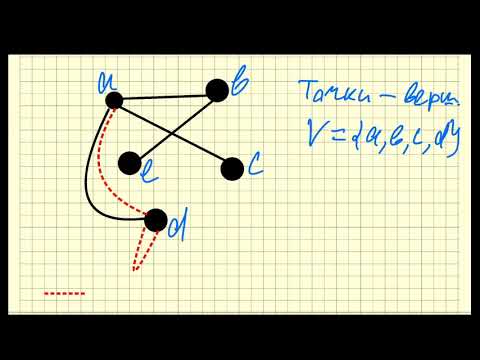
АЛКТГ-4. Графы I
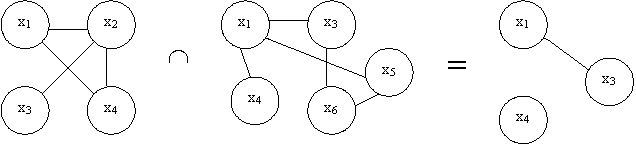

Применение теоремы о пересечении множества рёбер может существенно упростить задачу, особенно если графы представляют собой планарные объекты.
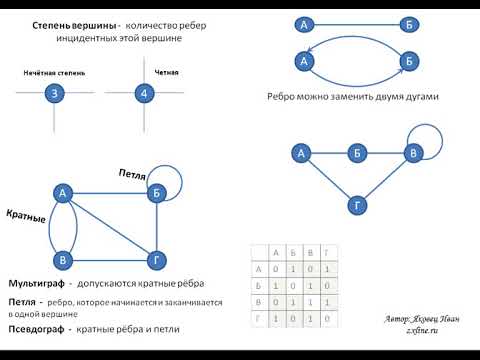
Графы, вершины, ребра, инцидентность, смежность
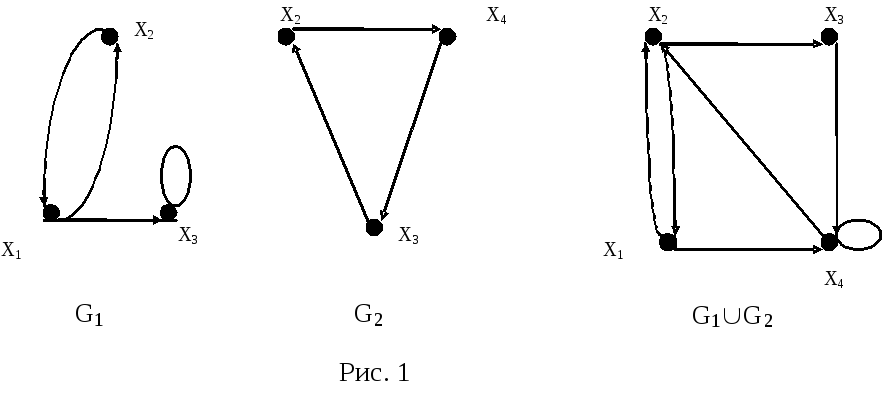
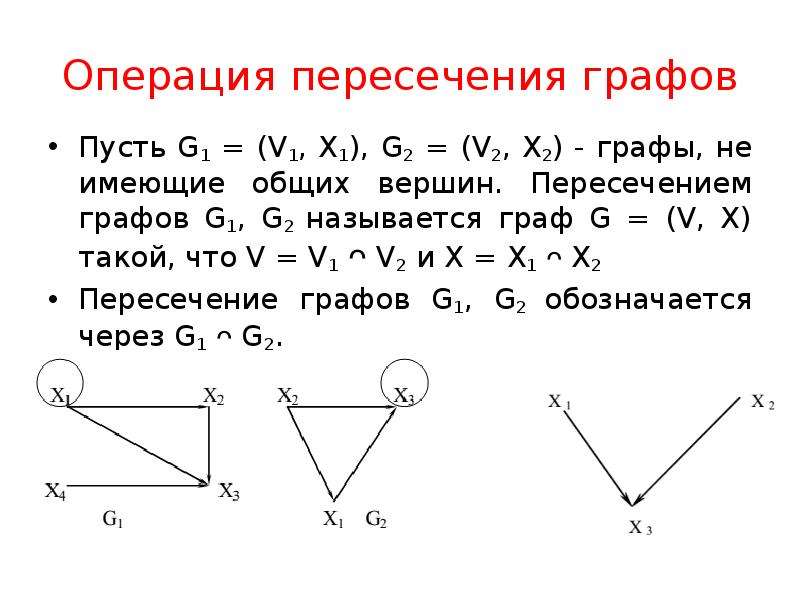
Не забывайте о принципах теории графов, таких как планарность и многогранность, которые могут быть полезны при анализе пересечений.
Флаги ''Пересечения'', ''Доп точки'', ''Исп пройденные отрезки'', ''Отрисовка графа''
Для решения сложных задач на пересечение графов важно тщательно анализировать возможности редуцирования графов, сокращая количество рёбер без потери информации.

4.3 Операции над графами Гиперкубы
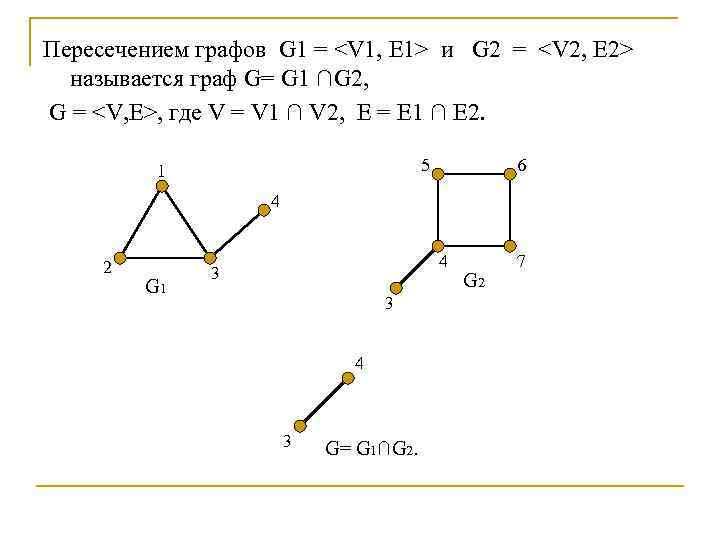
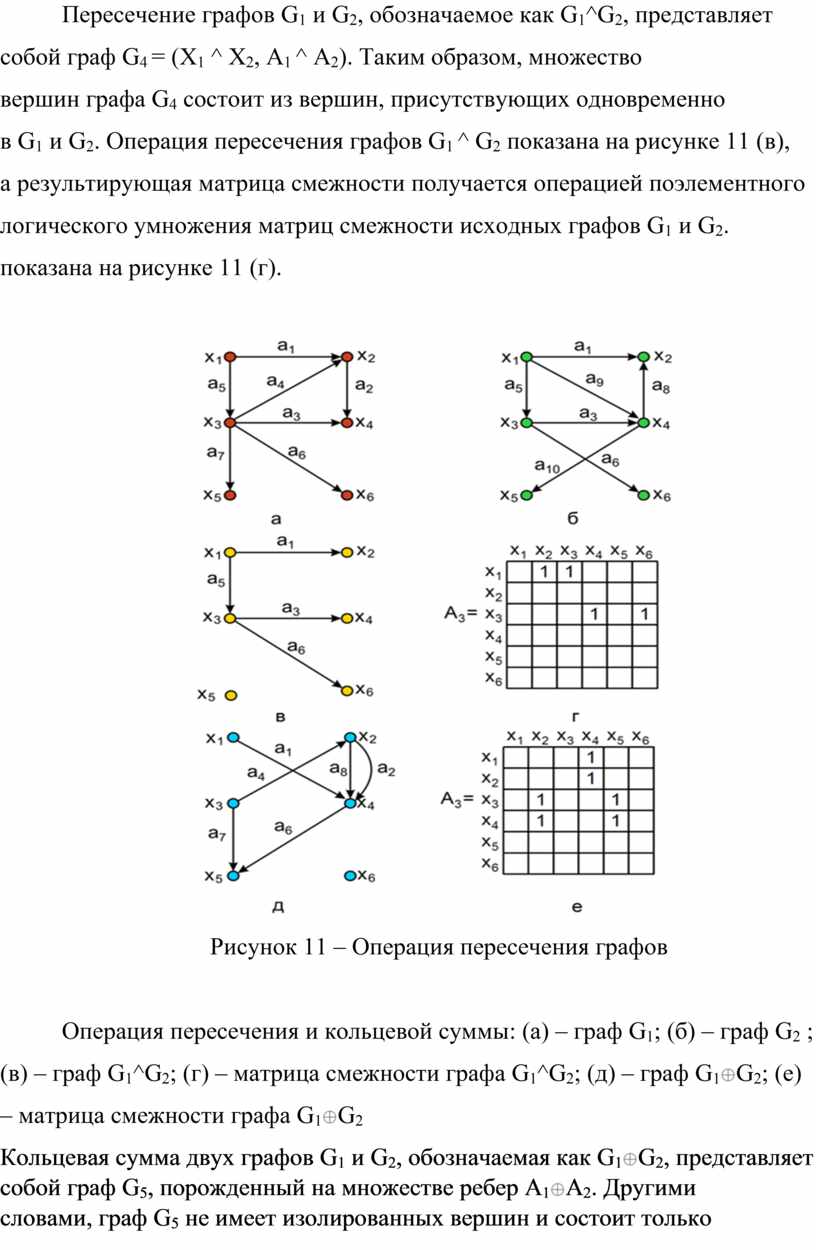
Отметьте, что задачи на пересечение графов могут требовать учета дополнительных ограничений, таких как минимизация числа пересечений или оптимизация расстояний между вершинами.


Использование динамического программирования может быть полезным инструментом для решения задач, связанных с минимизацией пересечений.
Лекция по дискретной математике №likerkacinema.ru теории графов. Изоморфные, обыкновенные, неориентированные
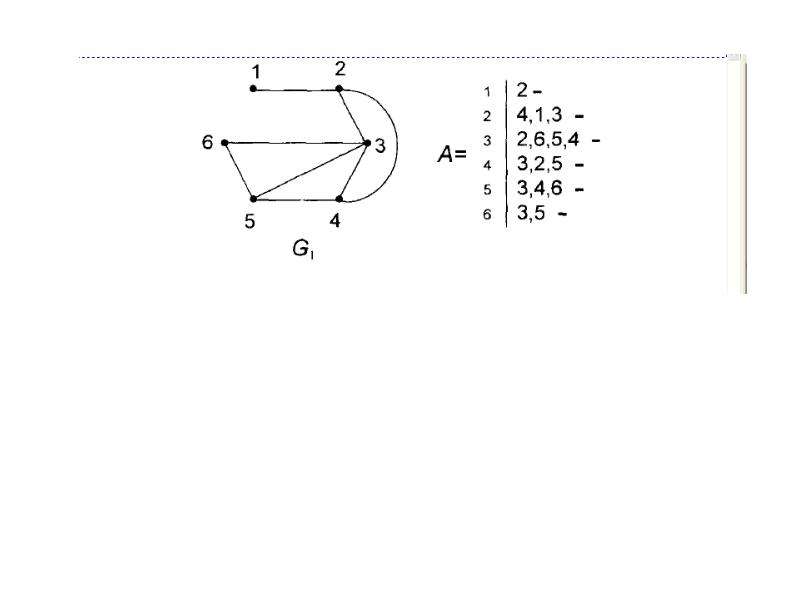
Если задача предполагает множество пересечений, полезно применять методы, которые помогут избежать излишних повторений и ускорят процесс вычислений.

Информатика. графы за 40 секунд!
Графы с переменными пересечениями часто решаются с помощью специализированных алгоритмов, таких как алгоритм Краскала или Прима.

Задачи по теории графов. 6 класс
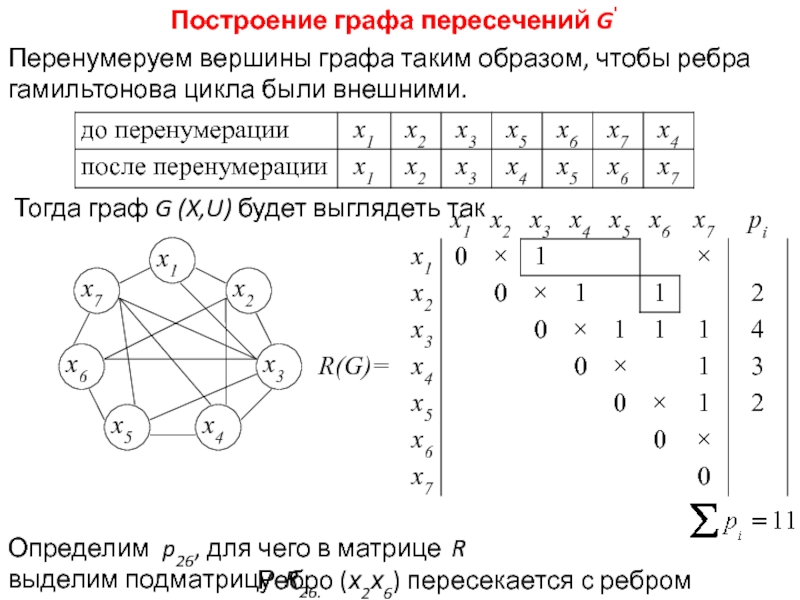
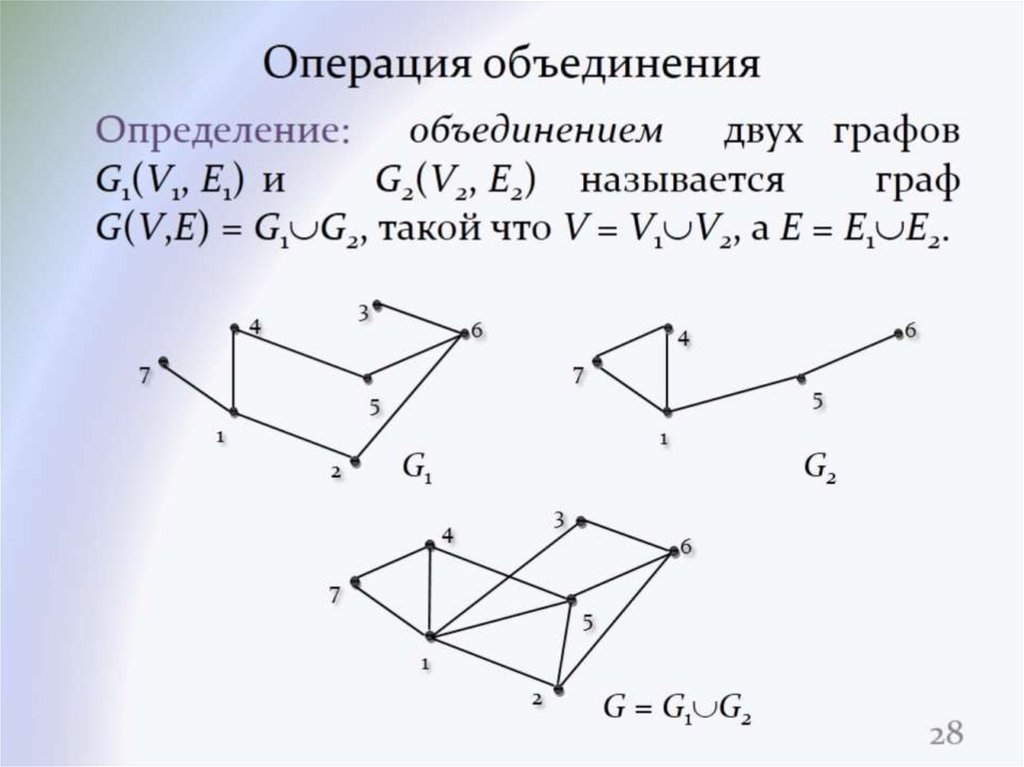
Не забывайте проверять результат, чтобы убедиться в правильности пересечений, а также в отсутствии ненужных или лишних соединений между вершинами и рёбрами.
