Понимание основы геометрических фигур и их важность для решения задач
Основание в геометрии — это одна из ключевых концепций, необходимая для правильного понимания и решения задач, связанных с фигурами, такими как треугольники, многоугольники и другие геометрические объекты. Разбираясь в этой теме, важно учитывать как теоретическую, так и практическую составляющую, чтобы успешно применять знания на практике. В этой подборке мы собрали полезные советы и рекомендации, которые помогут вам разобраться в основах геометрии и повысить уровень ваших знаний.
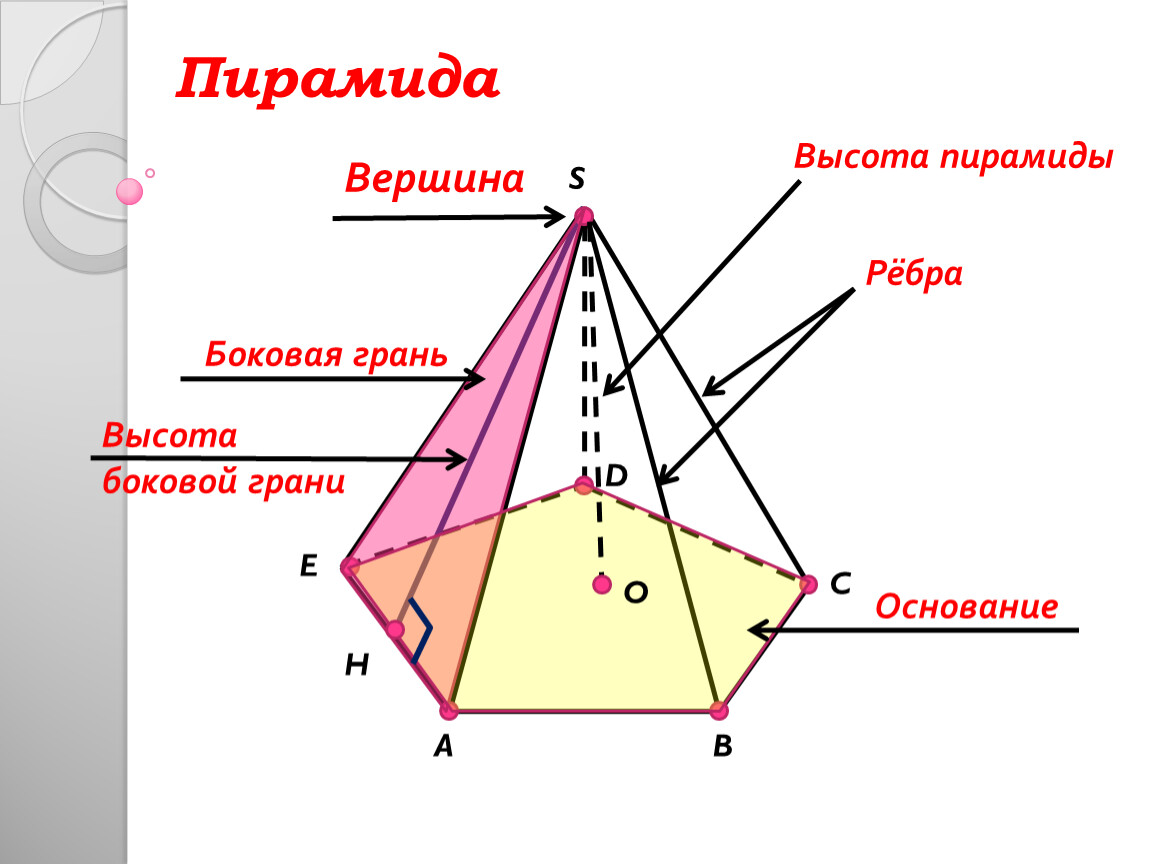
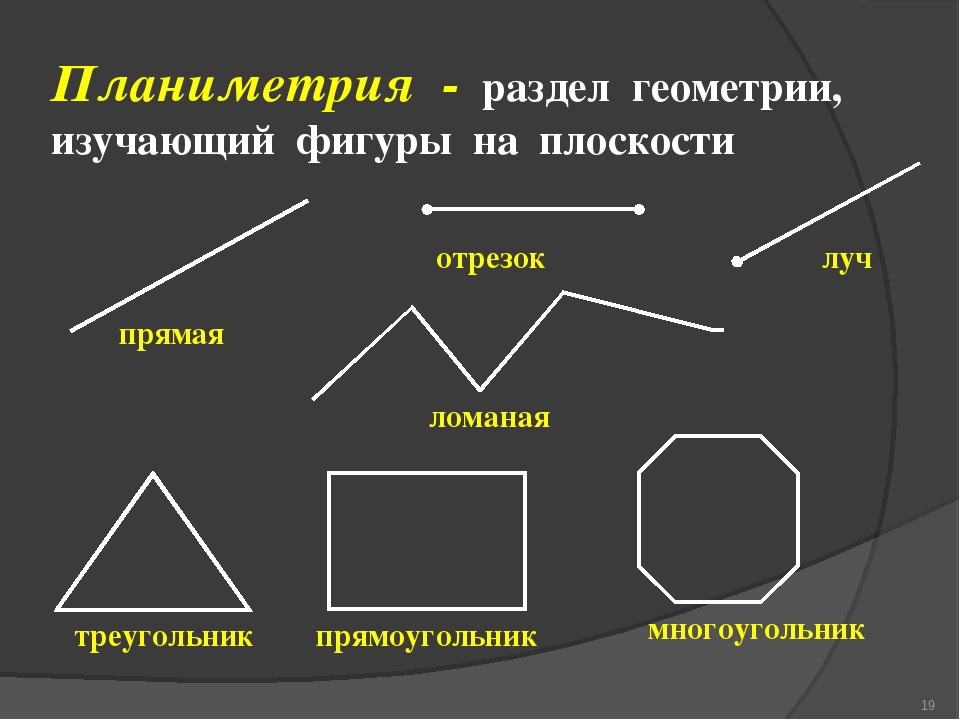

Основание треугольника — это любая из его сторон, выбранная для расчета площади. Обычно выбирается основание, которое наиболее удобно в контексте задачи.
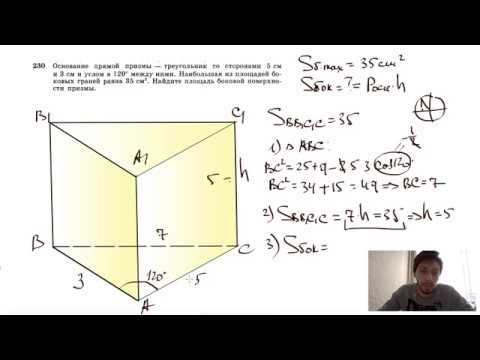
№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120
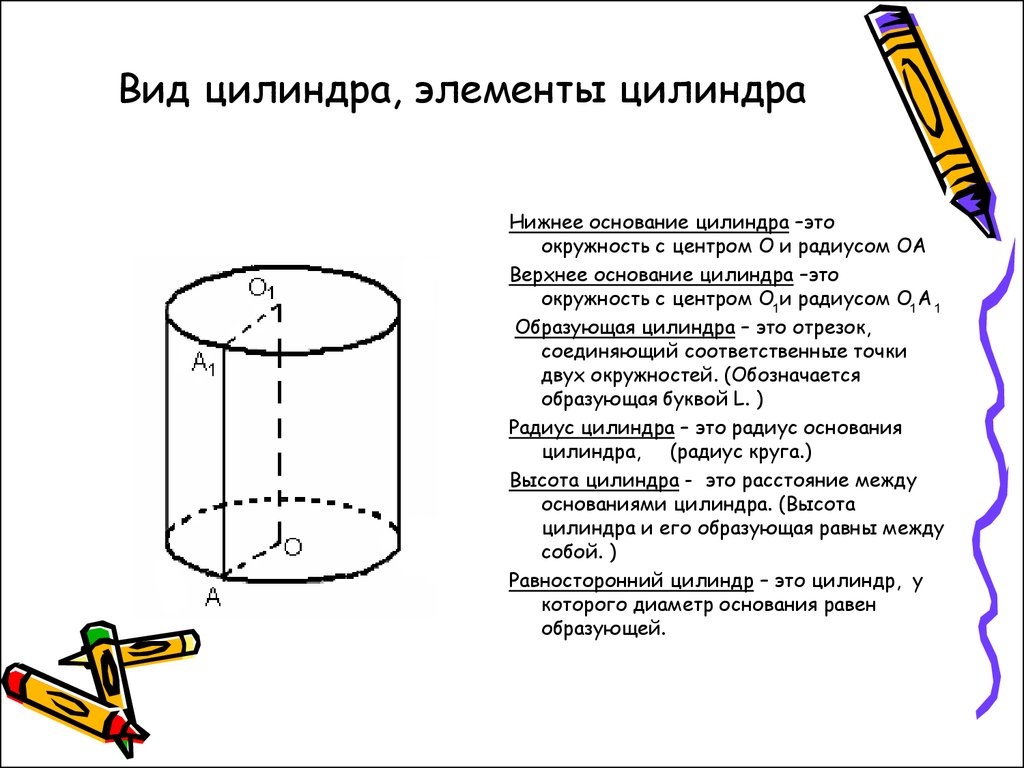
Для прямоугольных треугольников основание и высота — это перпендикулярные стороны, которые важны для вычисления площади.
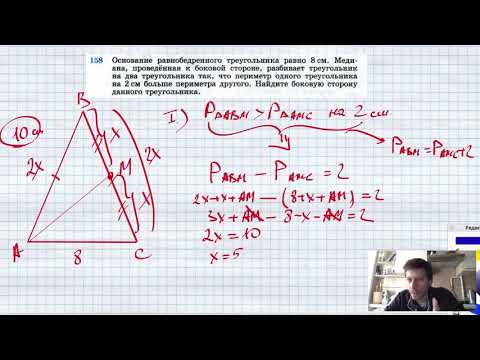
№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой стороне

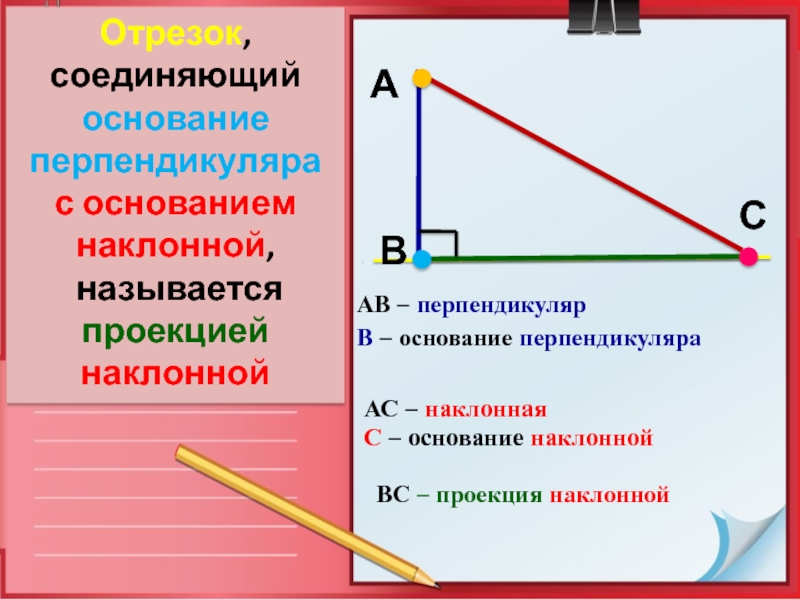
При решении задач на объемы геометрических тел важно помнить, что основание может быть не только прямой стороной, но и многогранной фигурой, например, многоугольником.

№219. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ
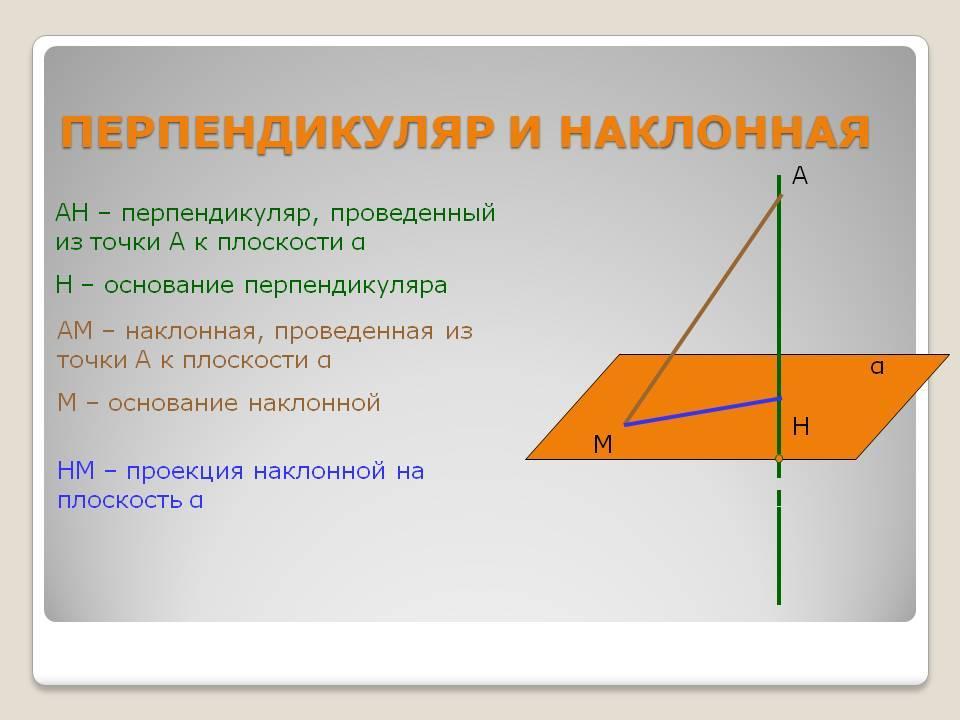
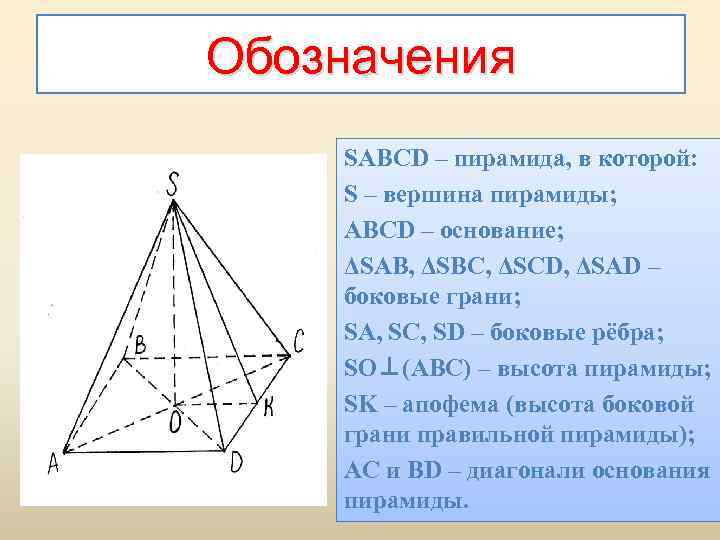
Основание прямоугольной призмы — это одна из ее граней, которая служит базой для вычисления объема.
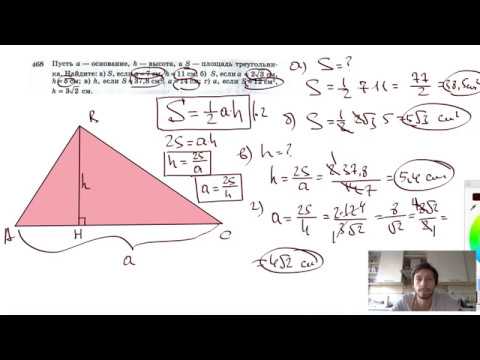
№468. Пусть а — основание, h — высота, a S — площадь треугольника. Найдите:
Не забывайте, что правильное определение основания является первым шагом для вычислений в геометрии, ведь от этого зависит выбор формул для решения задачи.

№799. Дана равнобедренная трапеция ABCD. Перпендикуляр, проведенный из вершины В к большему основани

Для нахождения площади круга основанием может быть радиус, который также играет важную роль при определении других характеристик фигуры.

likerkacinema.ru \


В задачах на многогранники основание может быть связано с любым элементом фигуры — например, с плоской гранью, которая определяет форму и размеры тела.

NUET 2021 разбор [ Файл в описании ]
При расчете площади многоугольников важно помнить, что основание может меняться в зависимости от типа задачи и выбранной методики.

В некоторых задачах геометрия требует учета не только физического основания, но и специфических характеристик фигуры, таких как углы и вершины.
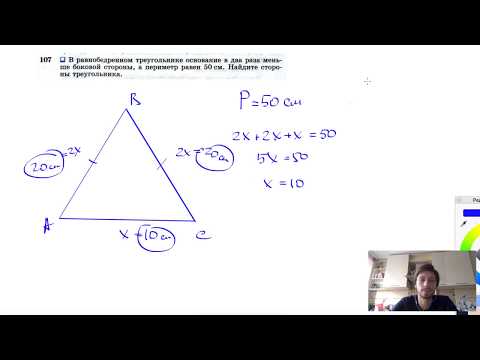
№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр
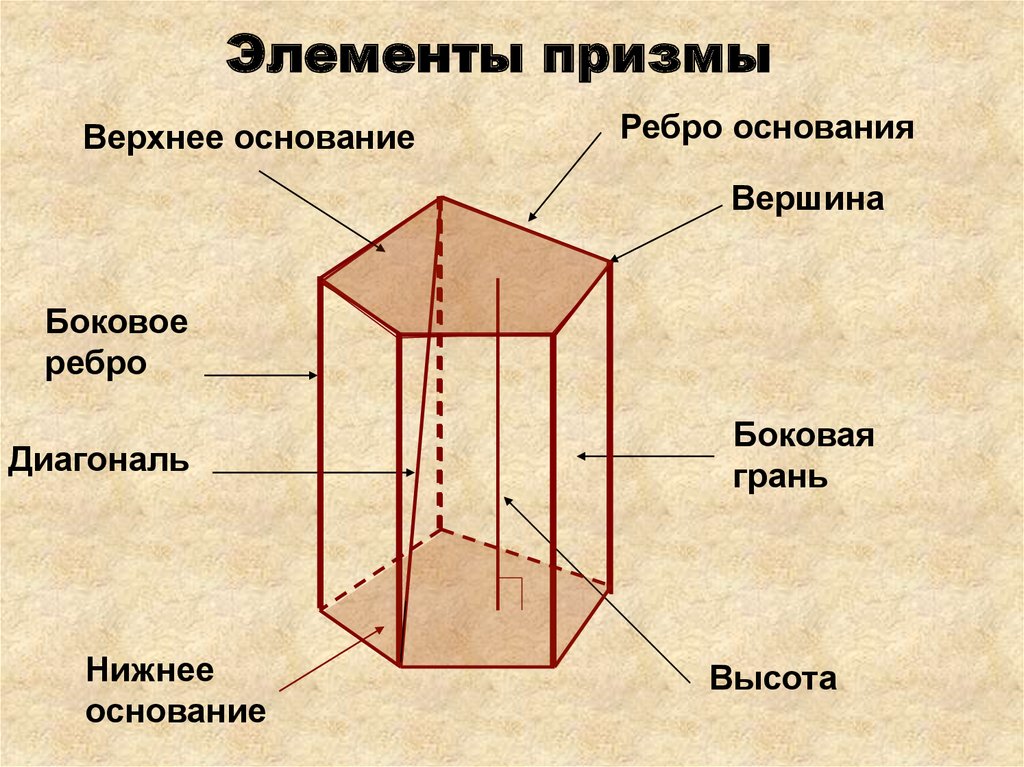
Основание может также изменяться в зависимости от того, с какой стороны смотреть на фигуру, что имеет значение при решении пространственных задач.

ГЕОМЕТРИЯ 7 класса с likerkacinema.ru рвет любой урок в школе
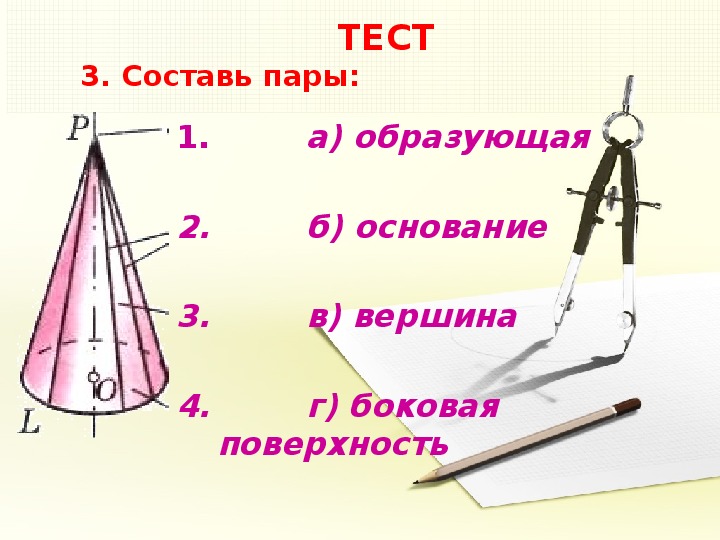

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы - Математика TutorOnline