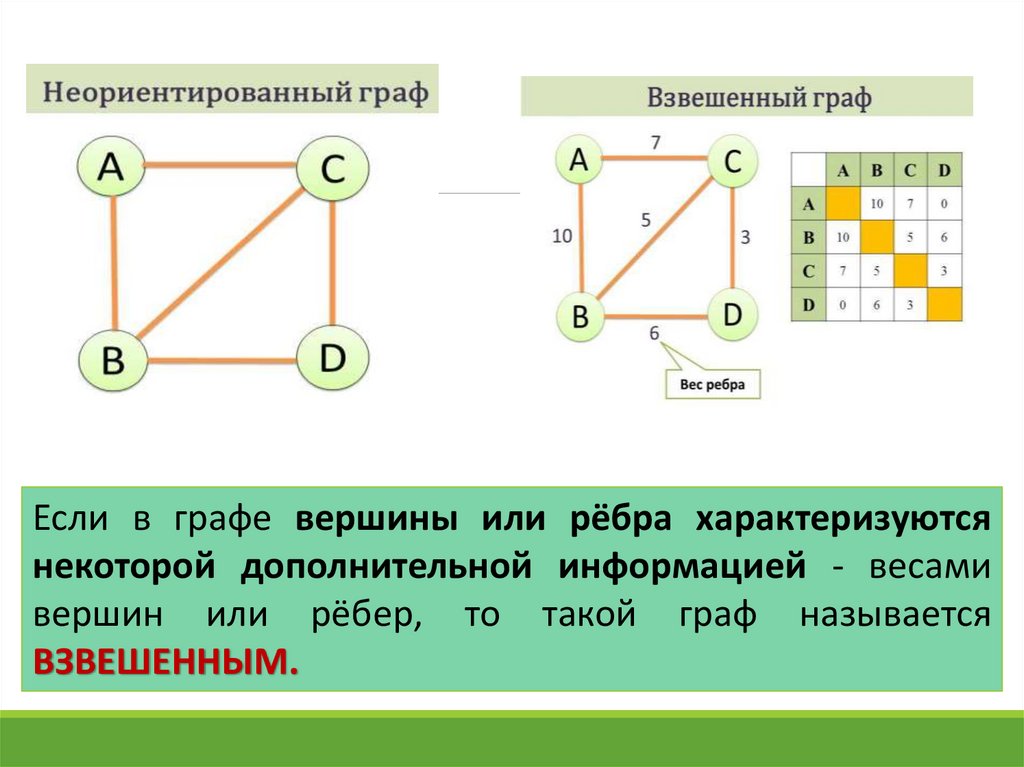
Ориентированные и взвешенные графы: основы и полезные советы по работе с деревьями
В этой статье мы рассмотрим основы ориентированных и взвешенных графов, а также их использование в различных задачах на графах, включая построение деревьев и поиск оптимальных решений. Узнайте, как эффективно работать с такими структурами данных и решать сложные задачи.

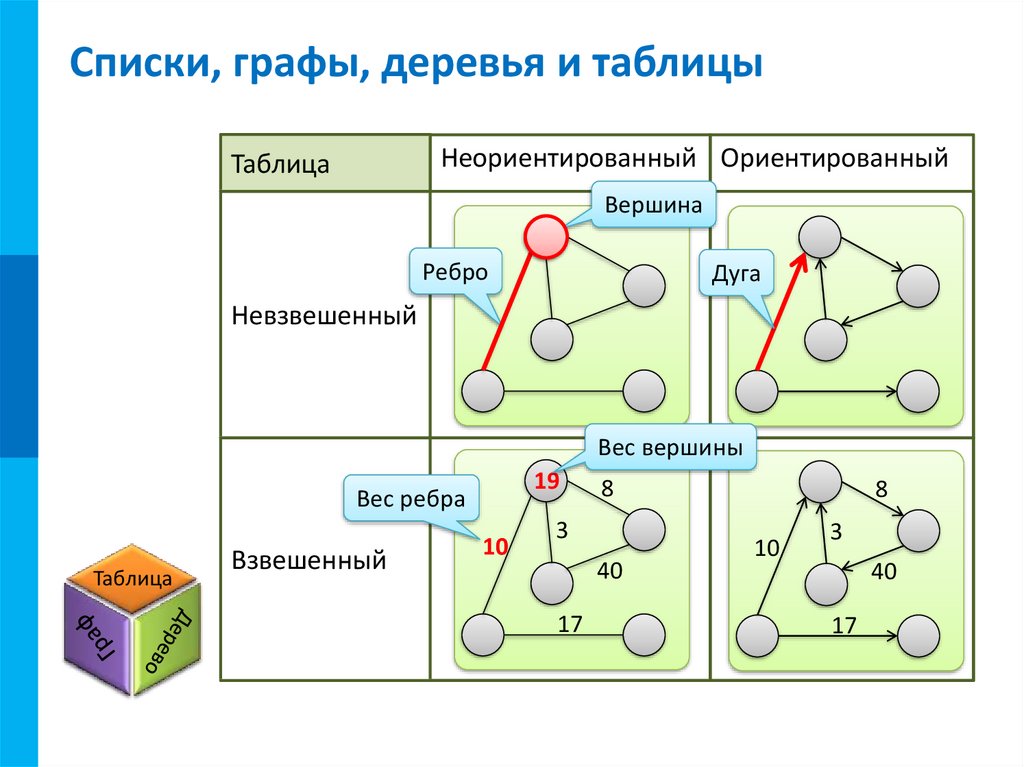
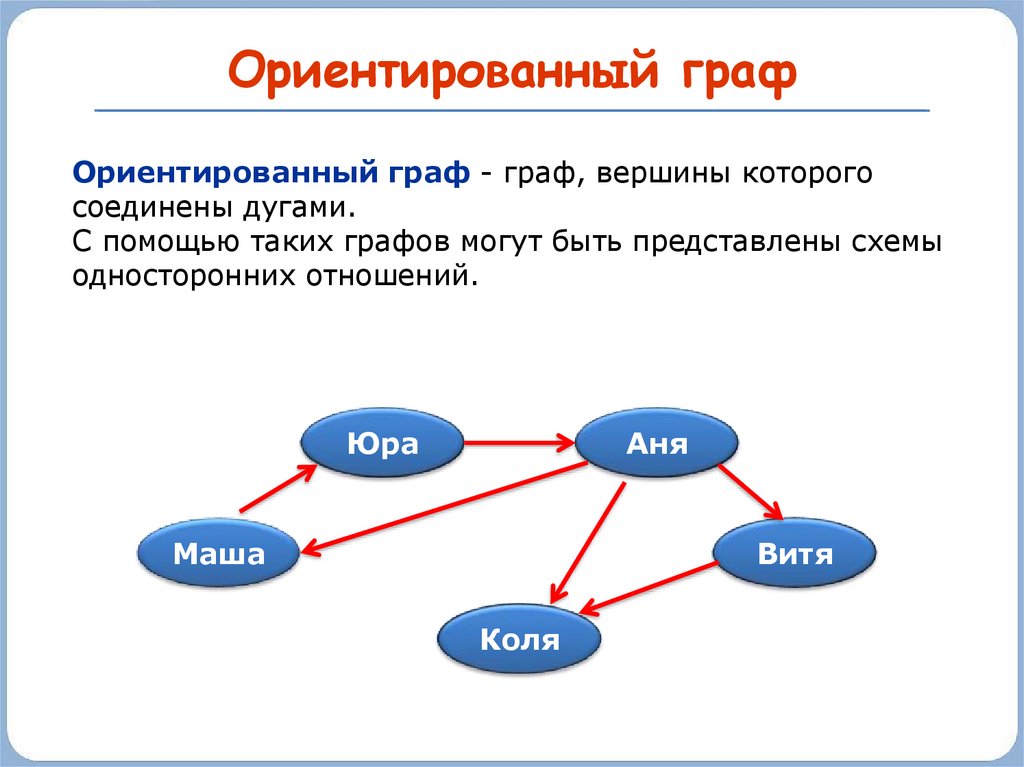
При работе с ориентированными графами важно учитывать направление рёбер, чтобы правильно моделировать взаимодействие элементов системы.
Решение задачи о кратчайшем пути Поиском решений (ориентированный граф)

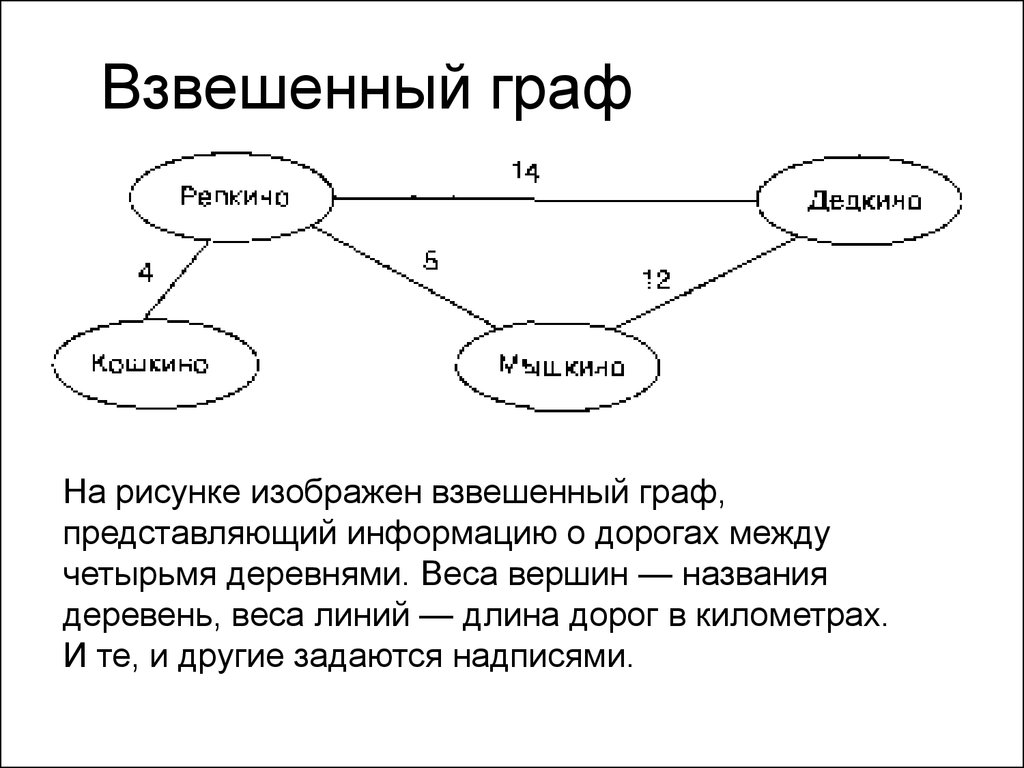
Использование взвешенных графов позволяет учитывать не только наличие связи, но и её «стоимость», что помогает при поиске оптимальных путей.
Алгоритм минимального остовного дерева в ориентированном графе Часть 3/3 Запись занятия 2021 11 13
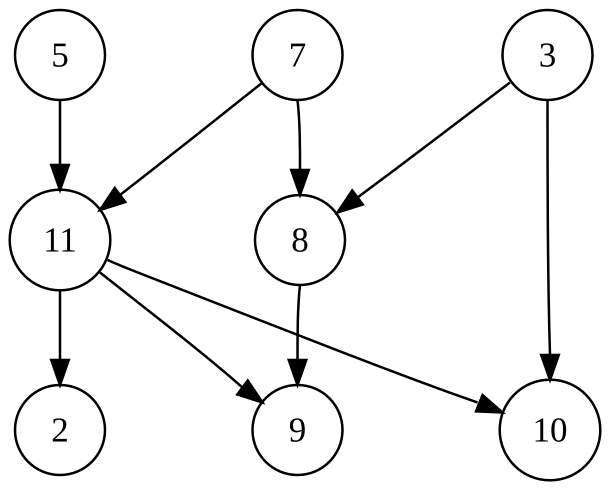
Дерево является частным случаем графа, где отсутствуют циклы, что упрощает решение задач поиска и минимизации.

Графы. Деревья. Остов графа
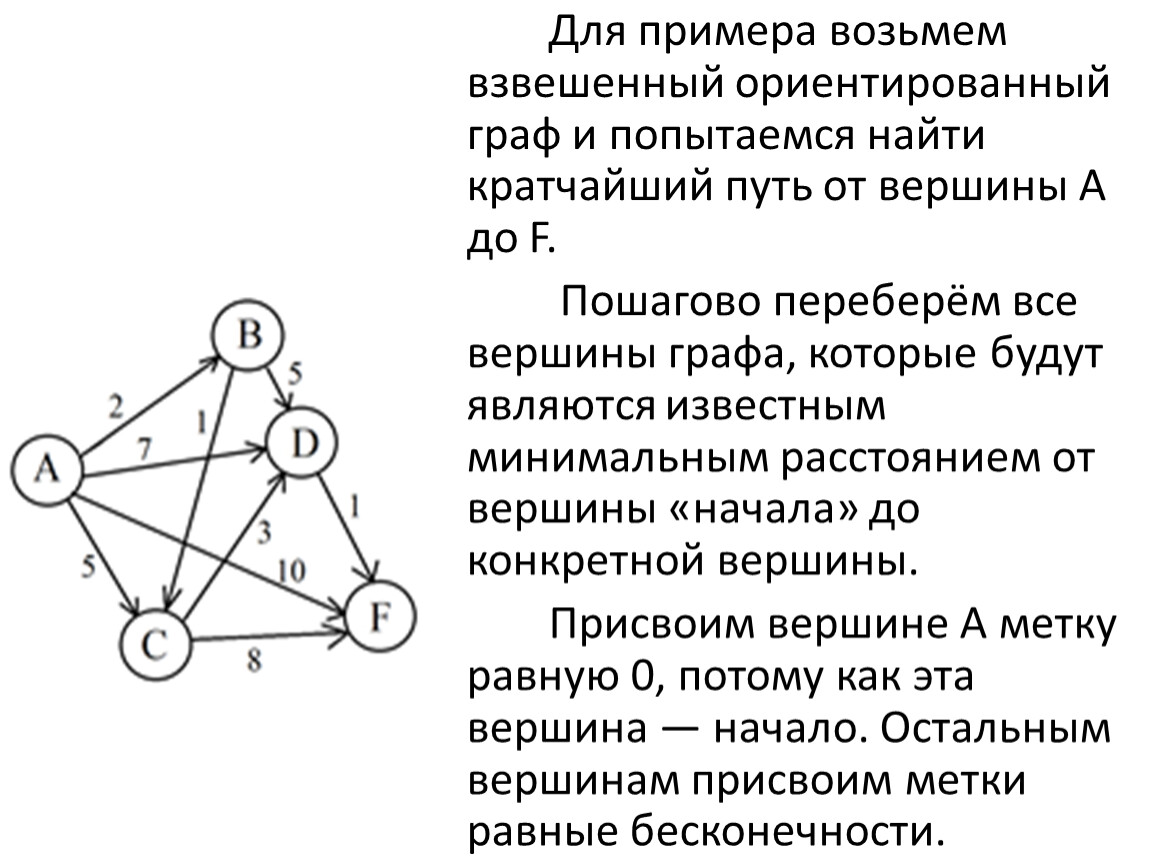
Для поиска кратчайшего пути в графе используйте алгоритм Дейкстры, который идеально работает с взвешенными графами.

Графы, Деревья и их обходы
Если ваш граф ориентирован, обязательно проверяйте возможные мертвые концы, которые могут возникать при неправильном учёте направлений рёбер.
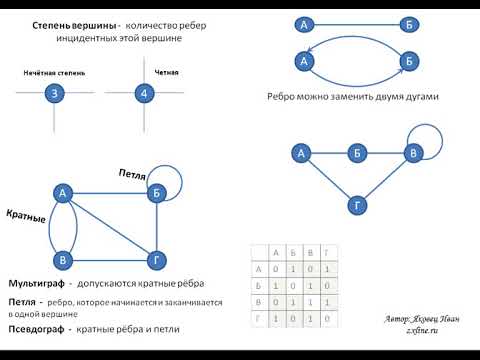
Графы, вершины, ребра, инцидентность, смежность
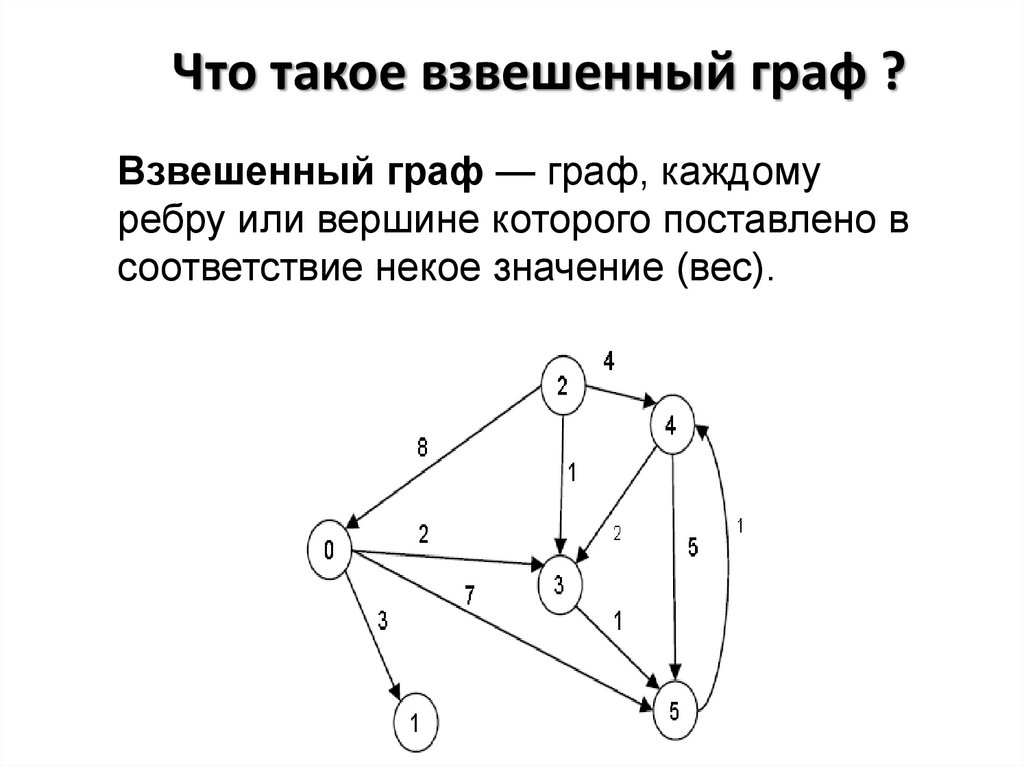
В случае построения дерева, важно выбирать подходящее дерево поиска, например, сбалансированное дерево для эффективного поиска и вставки элементов.

Графы для программистов

При работе с большими графами используйте оптимизации, такие как алгоритм A* для поиска кратчайшего пути с учётом эвристик.

КАК РАБОТАЮТ ГРАФЫ - СТРУКТУРЫ ДАННЫХ
Для определения связности графа используйте алгоритм поиска в глубину или ширину, чтобы эффективно найти компоненты связности.
Для работы с деревьями и графами важно правильно учитывать особенности памяти, особенно при хранении больших графов.
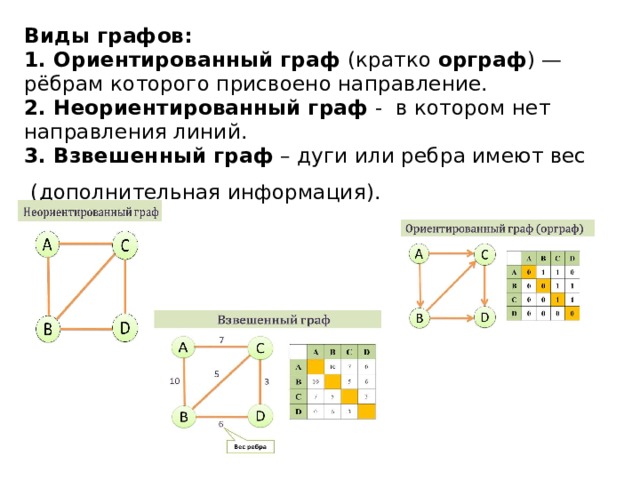

Не забывайте проверять наличие циклов в ориентированных графах, так как это может повлиять на алгоритмы поиска пути или топологическую сортировку.