Решение систем уравнений с использованием определителя третьего порядка по методу Крамера
Этот метод позволяет найти решения системы линейных уравнений с тремя переменными, используя детерминант матрицы коэффициентов и вспомогательные определители. Подробно объясняется, как вычислять такие детерминанты и использовать их для получения точных решений.



Убедитесь, что система уравнений имеет уникальное решение, проверив, что определитель матрицы коэффициентов не равен нулю.

Решение системы линейных уравнений третьего порядка методом Крамера


Для вычисления каждого из вспомогательных определителей заменяйте столбцы матрицы коэффициентов на столбцы свободных членов, соответствующие переменной.

Определитель третьего порядка. Метод Крамера.
Применяйте метод Крамера только в том случае, если матрица коэффициентов квадратная и имеет ненулевой определитель.

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математика


Для быстрого вычисления детерминантов используйте методы разложения по строкам или столбцам, чтобы минимизировать количество вычислений.
Математика Без Ху%!ни. Система линейных уравнений. Метод Крамера.

В случае сложных вычислений рассмотрите использование калькуляторов или специализированных программных средств для нахождения определителей.

Доказательство формул Крамера для системы двух уравнений

Проверяйте результаты с помощью других методов решения системы, чтобы убедиться в их корректности.
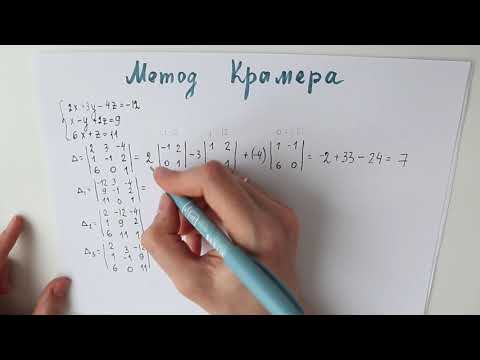
Решение систем линейных алгебраических уравнений методом Крамера.


При расчете определителей большого порядка используйте упрощенные методы, такие как правило Саррюса для матриц 3x3.

Не забывайте, что если определитель матрицы равен нулю, система уравнений либо не имеет решений, либо имеет бесконечно много решений.

Решение системы уравнений методом Крамера.

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvy
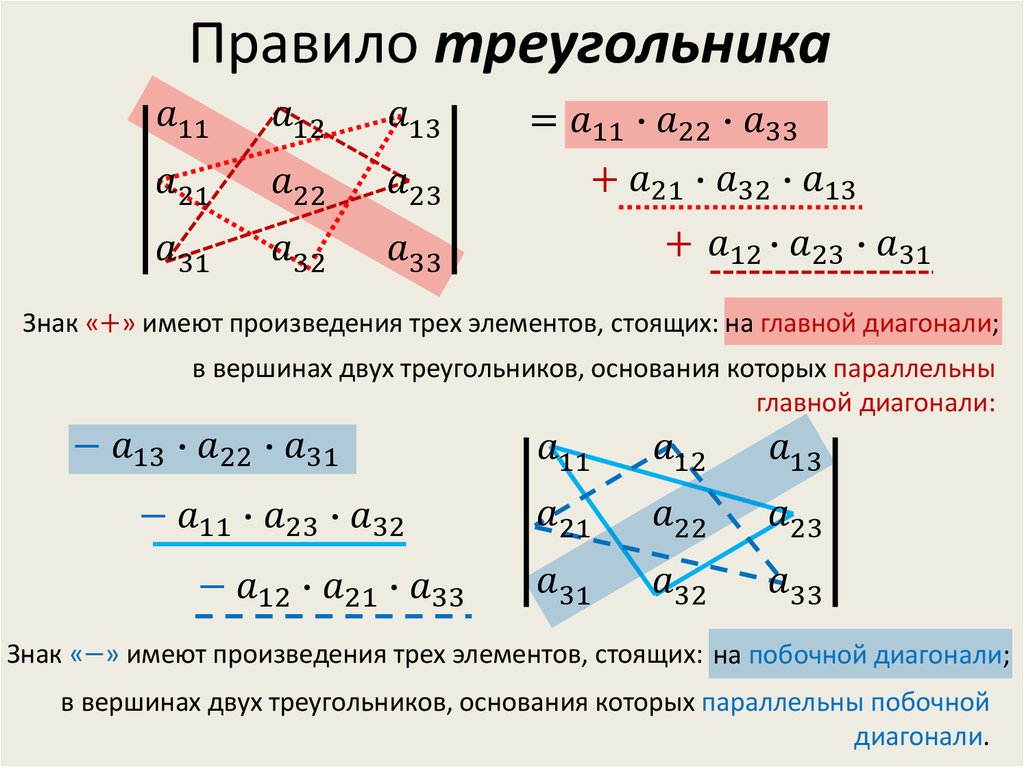
Метод Крамера работает только для систем с одинаковым числом уравнений и переменных, то есть для квадратных матриц.
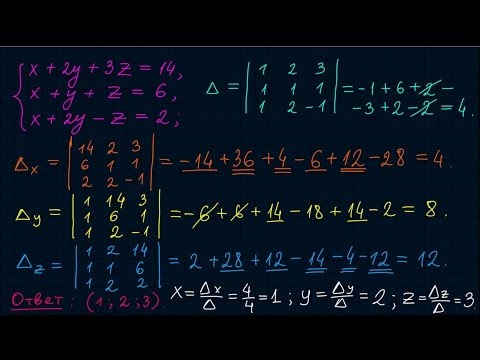
Решение системы трех уравнений по формулам Крамера

После нахождения значений переменных всегда подставляйте их обратно в исходную систему уравнений, чтобы убедиться в правильности решения.

2 минуты на формулы Крамера ➜ Решение систем уравнений методом Крамера
