Как предел интегральной суммы становится определенным интегралом: подробное объяснение
Определенный интеграл — это фундаментальное понятие математического анализа, которое имеет важное значение в различных областях науки и техники. Он определяется как предел интегральной суммы, что позволяет вычислять площадь под кривой функции на определенном интервале. Это описание поможет вам разобраться в этой теме и научиться решать задачи на определенные интегралы.



Для правильного понимания определенного интеграла полезно изучить интегральные суммы на простых примерах. Это поможет вам увидеть, как они приближаются к точному значению интеграла.

Вычислить определенный интеграл. Пример 2.


Не забывайте о геометрической интерпретации интеграла: он может быть использован для вычисления площади под кривой или длины дуги функции.

Определенный интеграл как предел интегральной суммы. Высшая математика.
Попробуйте визуализировать процесс вычисления интеграла, используя графики функции и прямоугольников, образующих интегральную сумму. Это поможет глубже понять процесс.
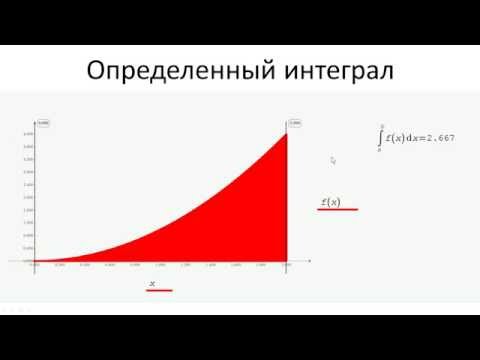
likerkacinema.ruва определенного интеграла

Понимание основ предела важно для работы с интегралами. Разберитесь, что такое предел последовательности, чтобы успешно применять его в контексте интегралов.

Определенный интеграл. 11 класс.


Изучите различные методы вычисления определенного интеграла, такие как метод подстановки и интегрирование по частям. Эти методы значительно упрощают решение сложных задач.

Понятие определенного интеграла, его геометрический смысл

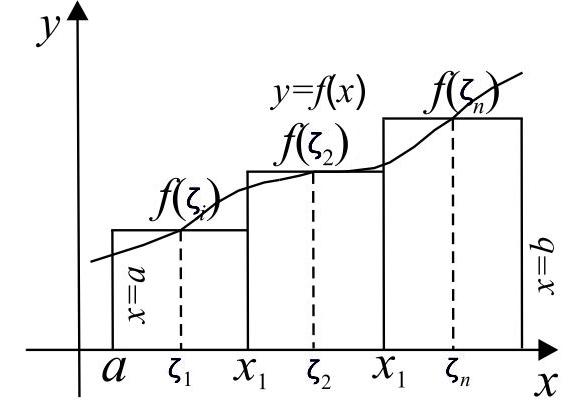
Чтобы лучше понять связь между пределом и интегралом, обратите внимание на теорему о среднем значении для определенного интеграла. Это важное средство для проверки ваших вычислений.

Линейность определенного интеграла. Ответы


Практика на примерах с различными функциями, такими как полиномы и тригонометрические функции, поможет закрепить ваши знания о вычислении определенных интегралов.
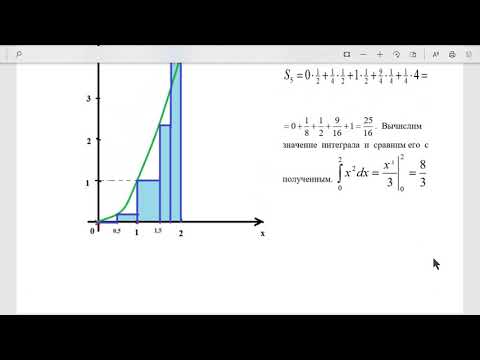
Интегрируемость по Риману Составление интегральных сумм

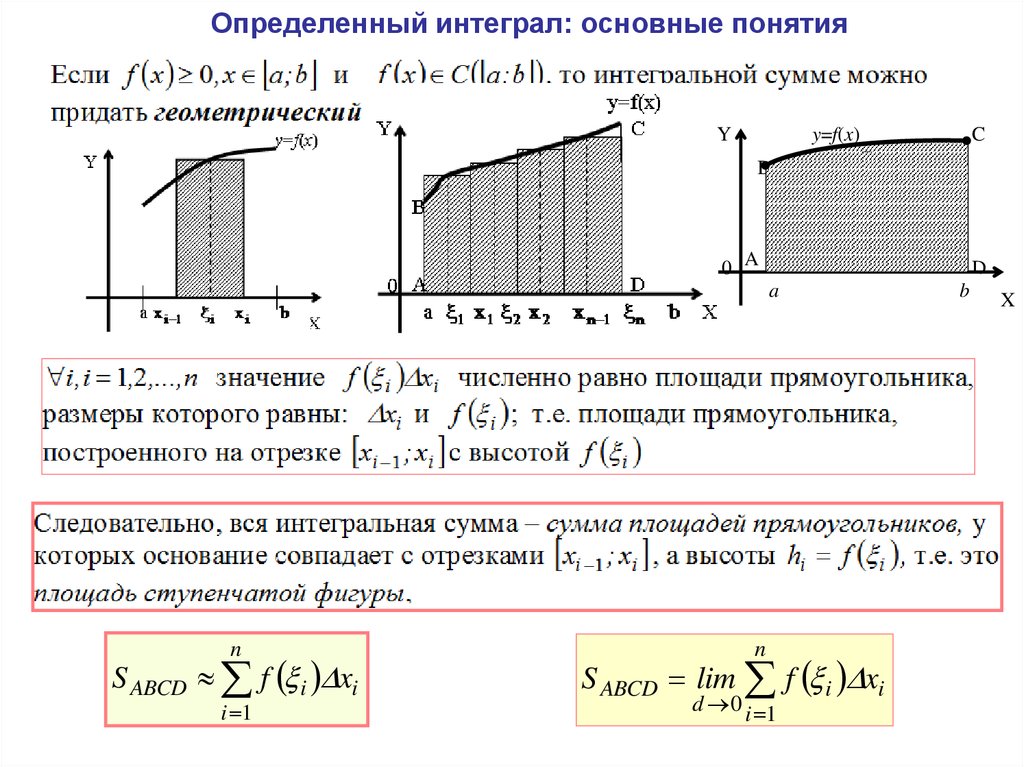
Не ограничивайтесь лишь стандартными задачами. Постарайтесь решать задачи с приложением интегралов, чтобы увидеть, как эта тема используется в реальных ситуациях, например, в физике и экономике.

Смысл интеграла и производной. В помощь студенту
Если вам трудно понять концепцию предела интегральной суммы, попробуйте проанализировать ее шаг за шагом, уменьшая размер промежутков между точками на интервале.

Для углубленного изучения интегралов полезно познакомиться с их свойствами, такими как линейность, аддитивность и пределы сумм. Эти свойства значительно упрощают решение задач.
