Советы и рекомендации по решению определенной системы уравнений с несколькими переменными
На этой странице мы рассмотрим полезные советы и методы решения различных типов систем уравнений, включая линейные и нелинейные. Вы узнаете, как правильно подойти к решению, используя как классические, так и более современные методы, а также советы для оптимизации процесса.



Для начала определите тип системы уравнений: линейная или нелинейная, это поможет выбрать правильный метод решения.

Совместные и несовместные, определенные и неопределенные системы линейных уравнений


Используйте метод подбора или подстановки для простых систем с двумя переменными, это позволит быстро получить решение.

Решение системы уравнений методом Гаусса

Для более сложных систем применяйте метод Гаусса или метод Крамера, которые подходят для линейных систем с несколькими переменными.

Решение систем уравнений. Методом подстановки. Выразить Y


Если у вас есть нелинейная система, попробуйте метод Ньютона или итерационный метод для нахождения приближенных решений.

Системы линейных уравнений. Метод Крамера


Всегда проверяйте полученные решения, подставив их в исходные уравнения, чтобы исключить ошибочные ответы.
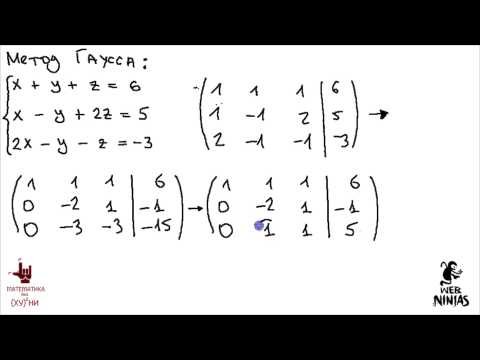
Математика без Ху%!ни. Метод Гаусса.


Если система содержит параметры, постарайтесь исследовать зависимость решений от этих параметров для более глубокого понимания проблемы.

Для экономии времени и точности используйте численные методы, если аналитическое решение слишком сложное или невозможно.

Определенные и неопределенные системы уравнений


Будьте внимательны при использовании матричных методов — они могут привести к ошибкам, если не учитывать особенности исходных данных.


Для систем с большим количеством уравнений используйте методы приближенных вычислений, такие как метод наименьших квадратов.

Лекция №likerkacinema.ruы исследования систем уравнений


Не забывайте об одном из самых важных аспектов: тщательная проверка промежуточных шагов может предотвратить многие ошибки в решении.

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.
