Геометрические свойства вписанной окружности в трапецию с прямым углом
В этой статье вы найдете описание свойств окружности, вписанной в прямоугольную трапецию, наглядные фотографии и полезные советы для понимания этой геометрической фигуры.
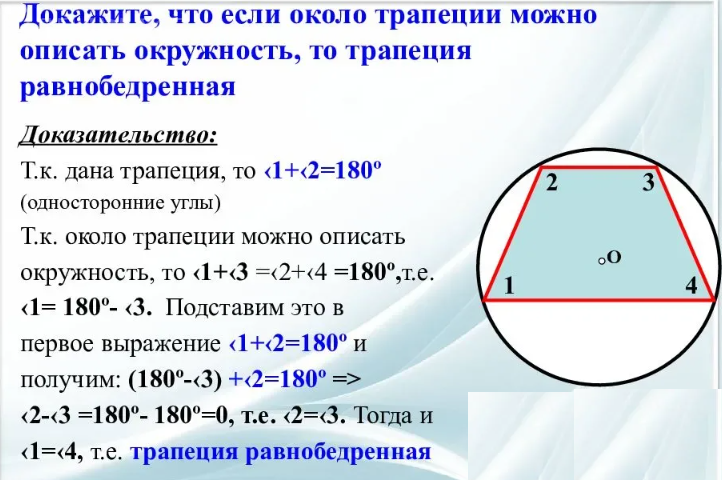
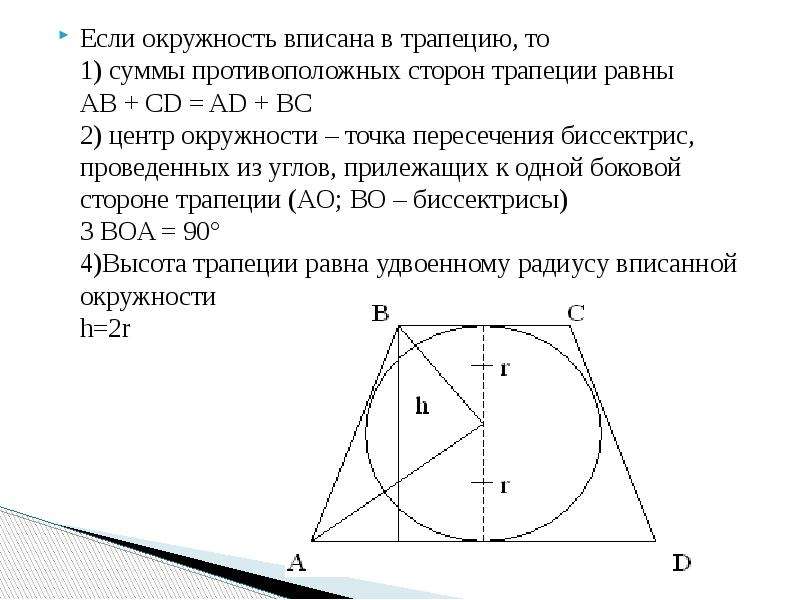
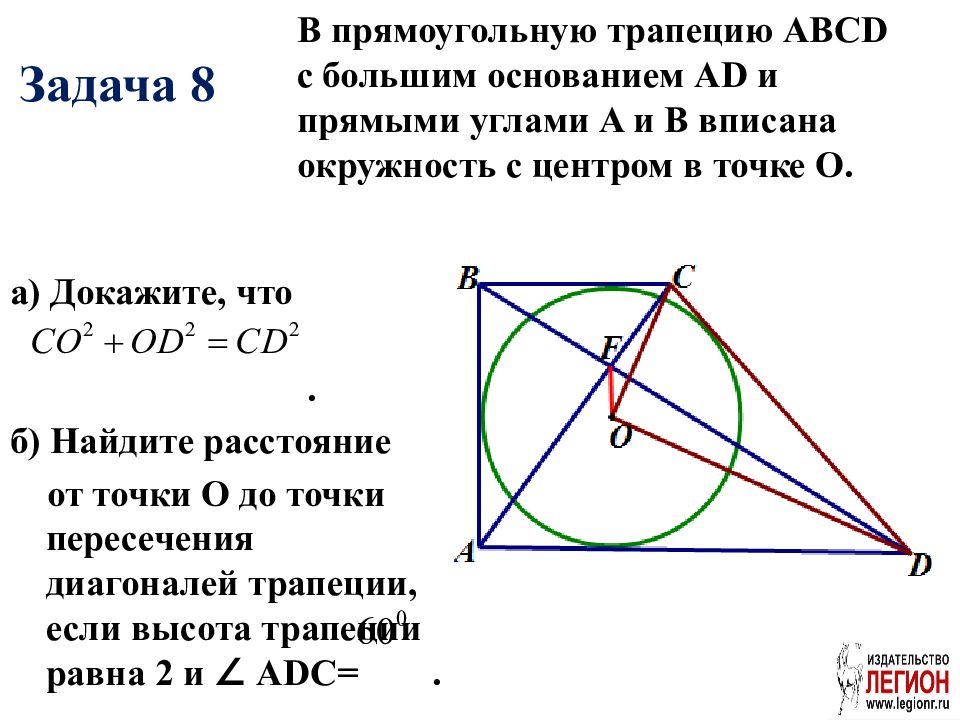
Для трапеции с окружностью важно, чтобы суммы её оснований равнялись суммам боковых сторон.

ЕГЭ ВПИСАННАЯ ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНУЮ ТРАПЕЦИЮ - ЗАДНИЙ ХОД В МАТЕМАТИКЕ ИЛИ КАКОЙ ТО ПОДВОХ -
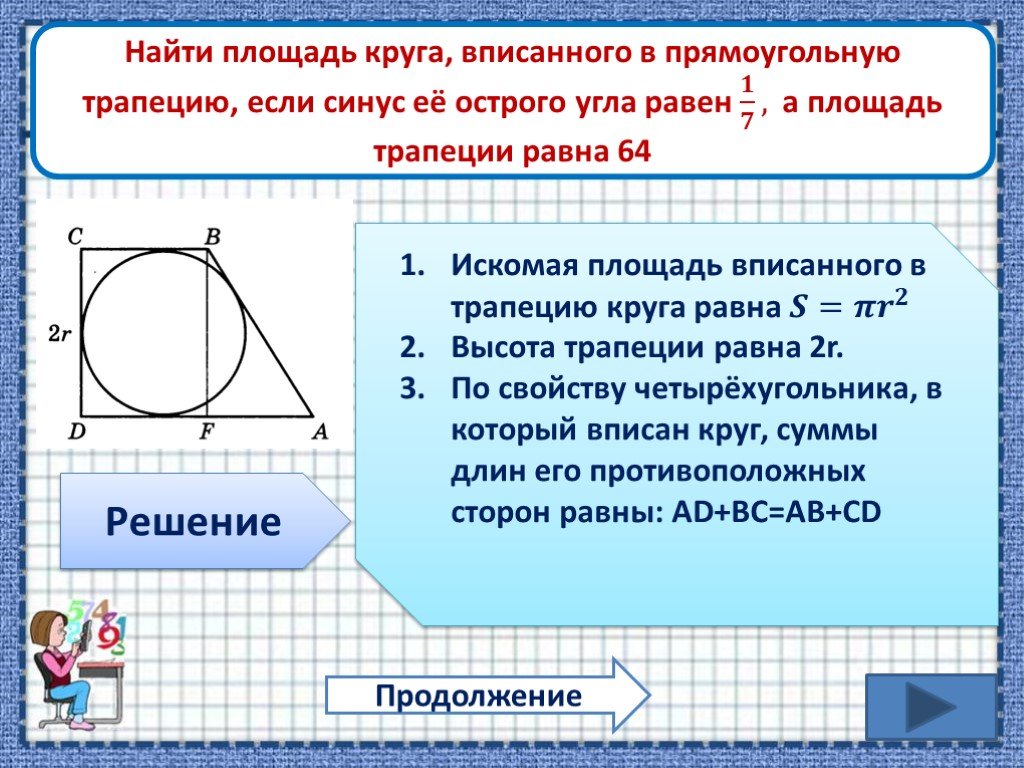
Центр вписанной окружности всегда лежит на пересечении биссектрис углов трапеции.
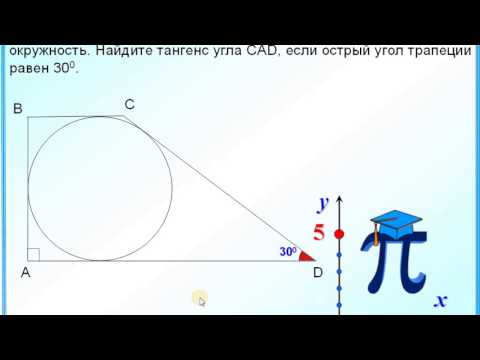
Задание 26 Описанная прямоугольная трапеция


Площадь прямоугольной трапеции можно найти через радиус вписанной окружности и полупериметр.
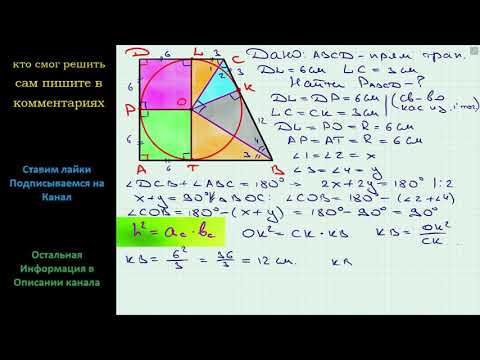
Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основание
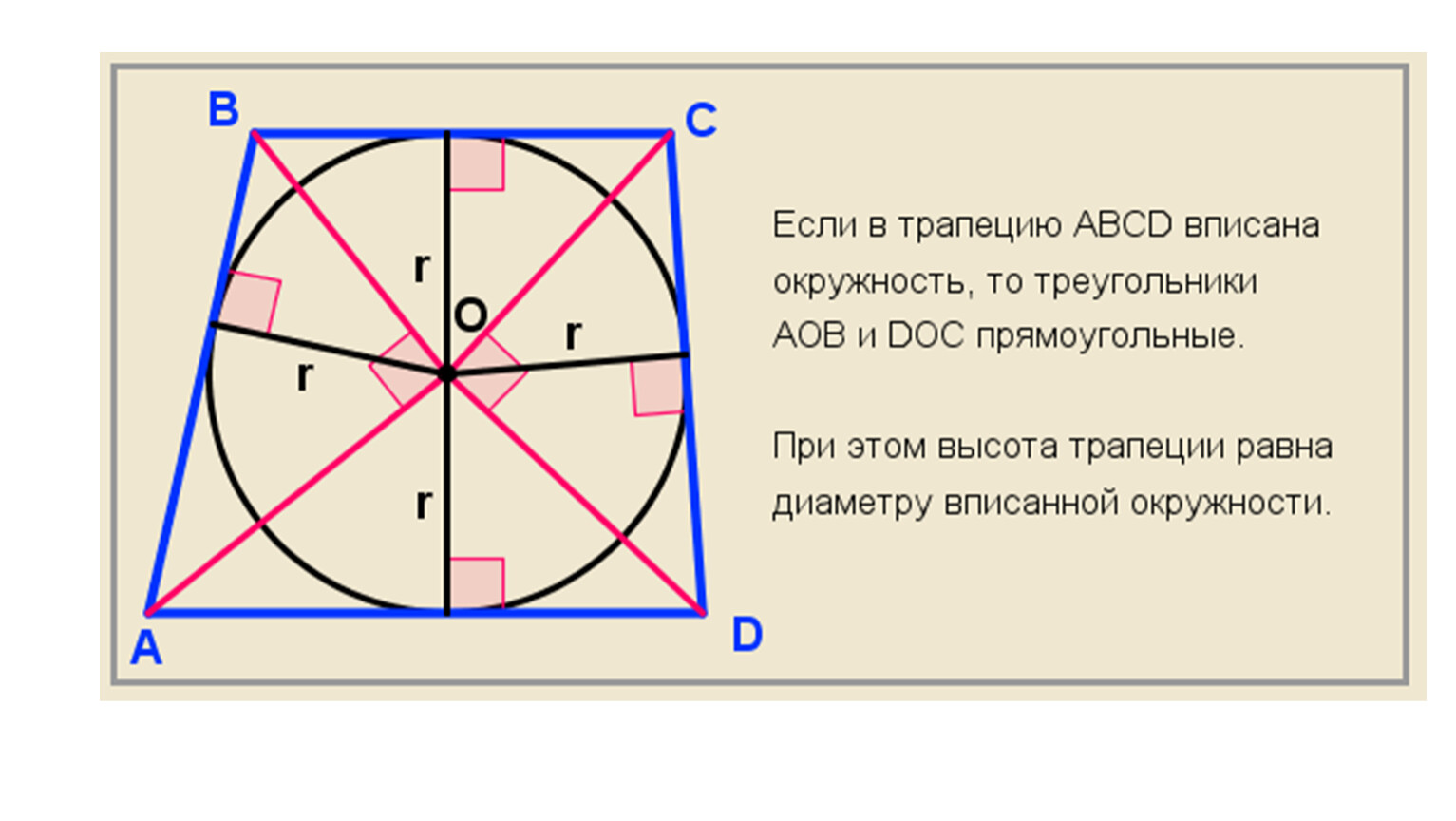
Радиус вписанной окружности равен отношению площади трапеции к её полупериметру.

Трапеция и вписанная окружность

Для построения трапеции с вписанной окружностью важно правильно задать размеры сторон.

Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делится

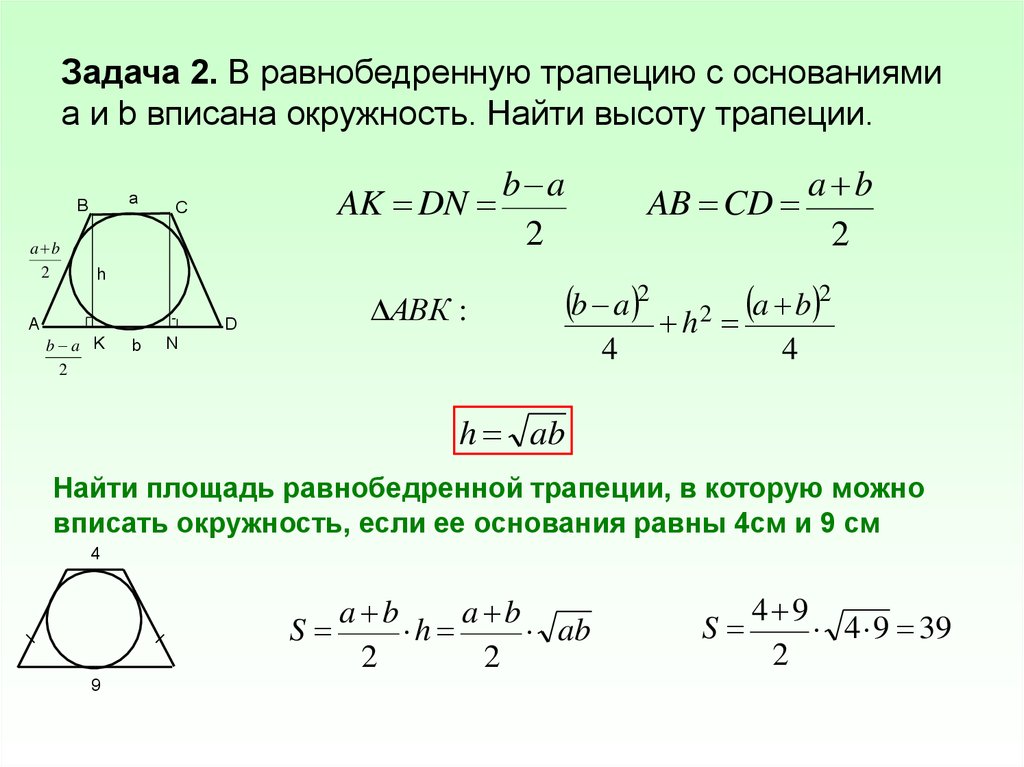
Если окружность вписывается, углы у основания боковых сторон равны.
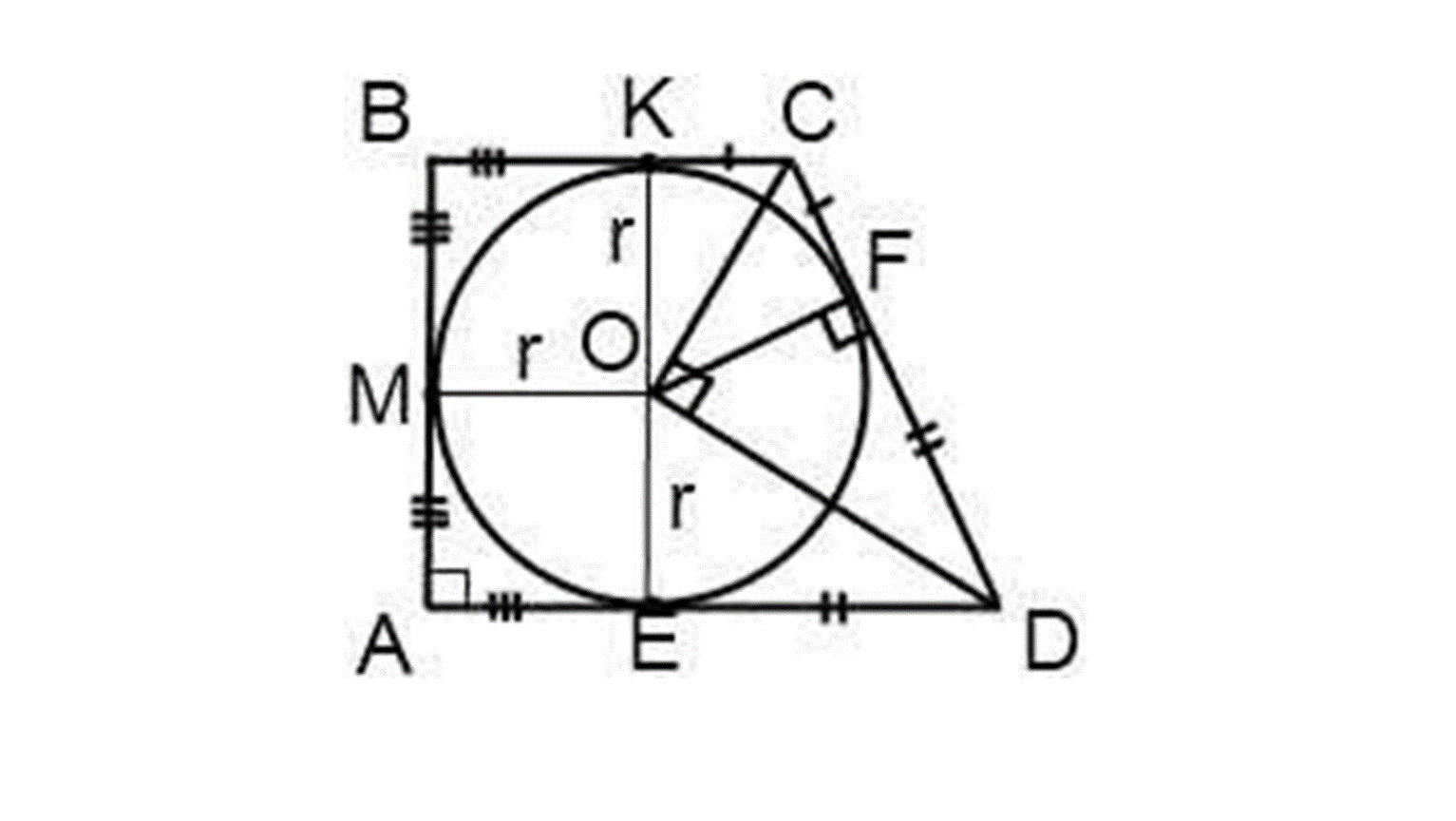
Используйте формулы для проверки правильности расчёта параметров трапеции с вписанной окружностью.
Помните, что диагонали такой трапеции пересекаются под углом, равным 90 градусов.
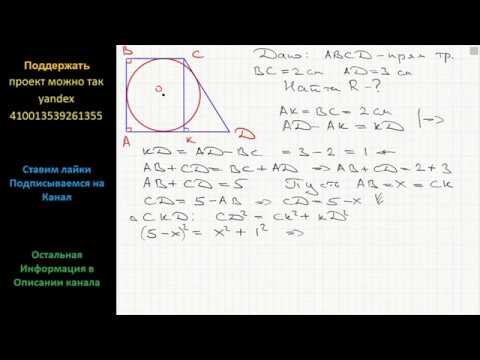
Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапеции

Внимательно изучите свойства касательных к окружности, вписанной в трапецию.

Геометрическая точность расчётов — залог правильного построения вписанной окружности.

Окружность и трапеция - ЕГЭ-2018. Задание 17. Математика. Профильный уровень - Борис Трушин +
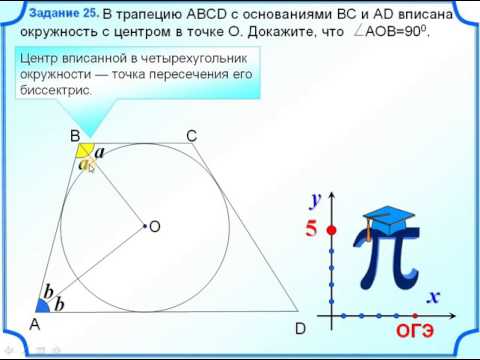
Задание 25 Описанная трапеция