Окружности, пересекающие стороны треугольника: важные геометрические свойства и их применение
Окружности, которые пересекают стороны треугольника, представляют собой важный элемент в геометрии, имеющий множество теоретических и практических применений. Рассмотрение таких окружностей позволяет глубже понять свойства треугольников и их взаимосвязь с другими геометрическими объектами. В этой статье мы разберем основные моменты, связанные с этим понятием, и поделимся полезными советами по изучению подобных фигур.
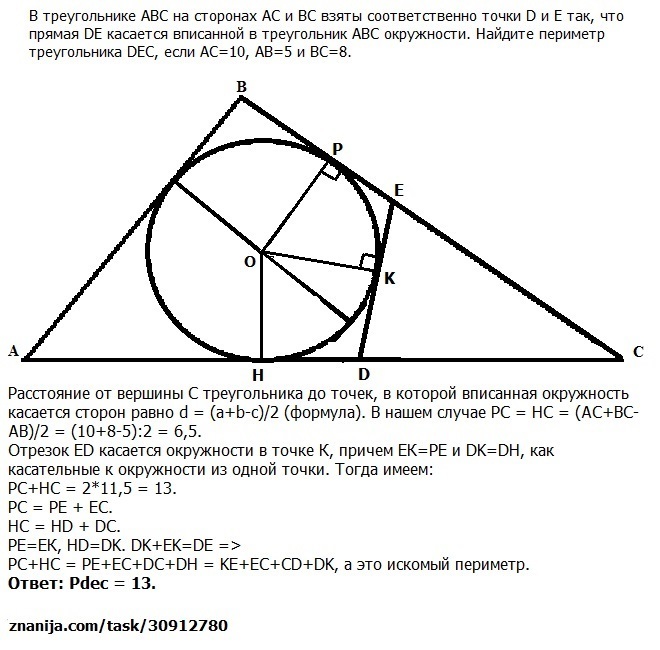
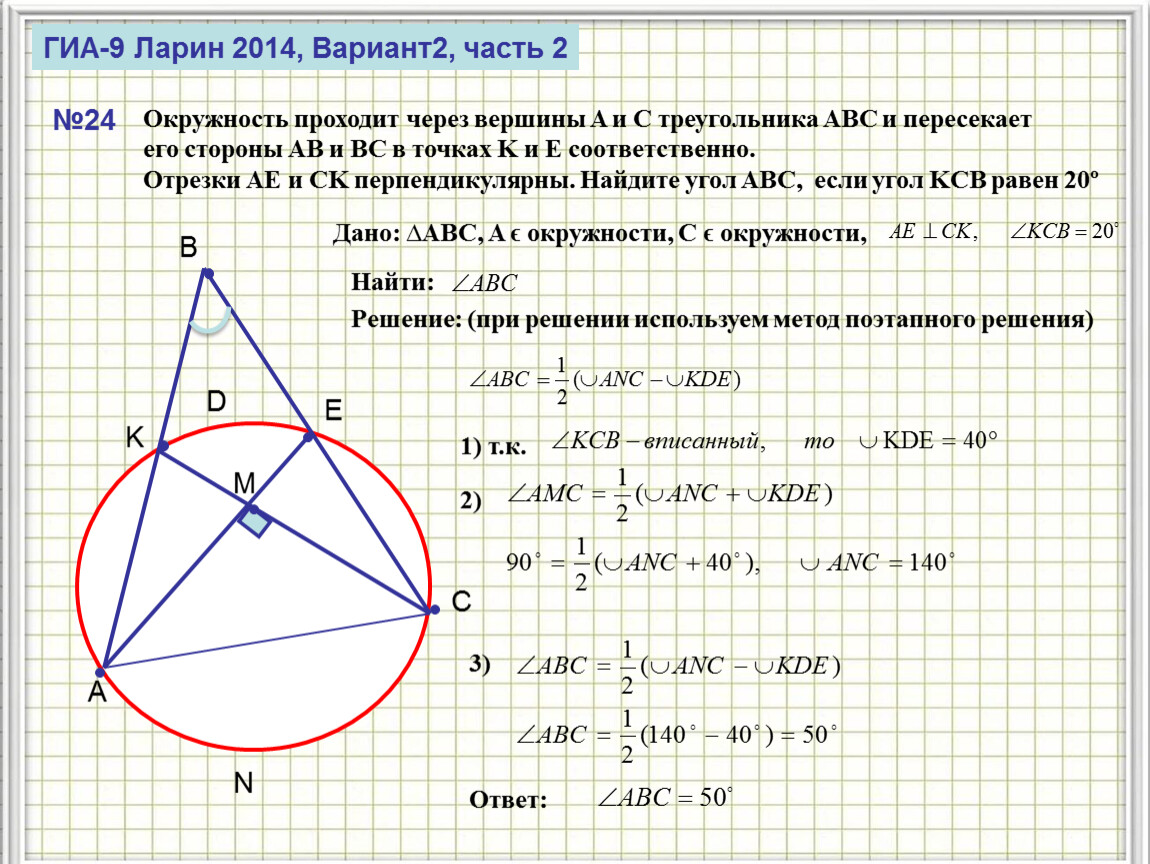

Для начала важно отметить, что окружности, пересекающие стороны треугольника, могут быть как вписанными, так и описанными, что зависит от их расположения.

Задание 11 Графики функций ОГЭ по математике 2024 Умскул

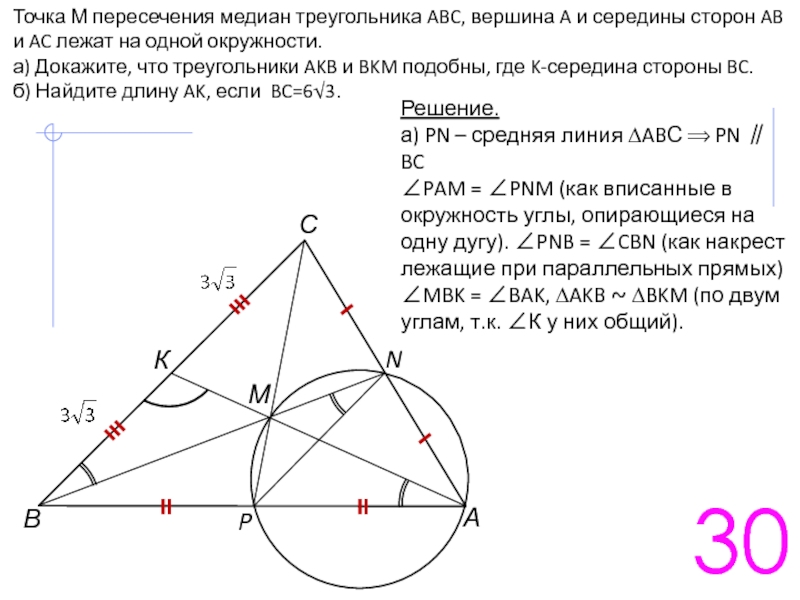
Одним из важных понятий является теорема о касательной к окружности, которая касается точек касания и углов, образующихся при пересечении с сторонами треугольника.
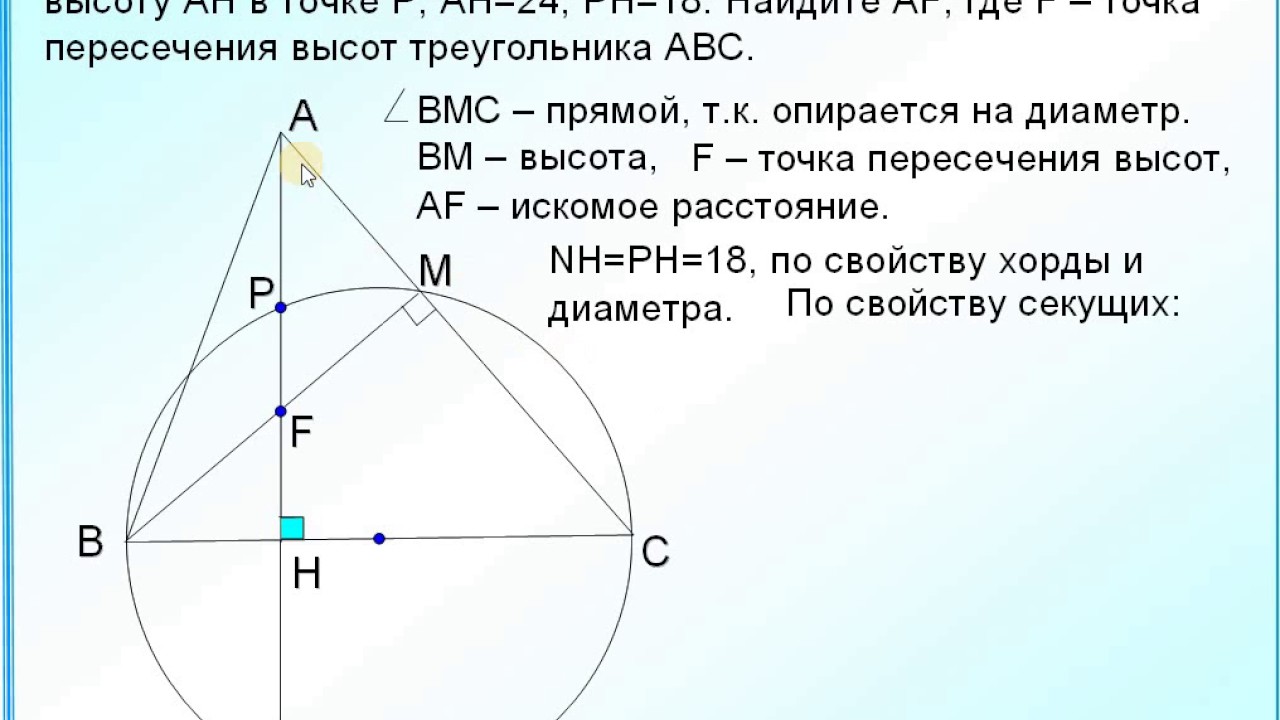
Окружность пересекает стороны АВ и АС треугольника ABC в точках N и Р соответственно - №11438
Если окружность касается одной из сторон треугольника, то существует правило для вычисления расстояния от этой точки до углов, которые могут быть полезными для решения задач.
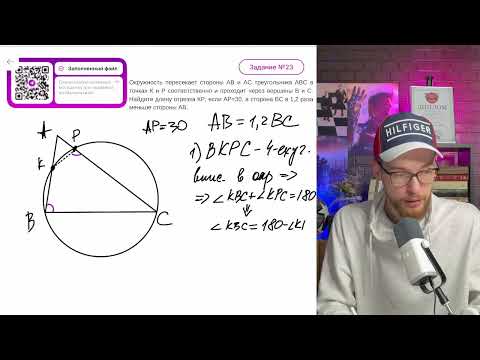
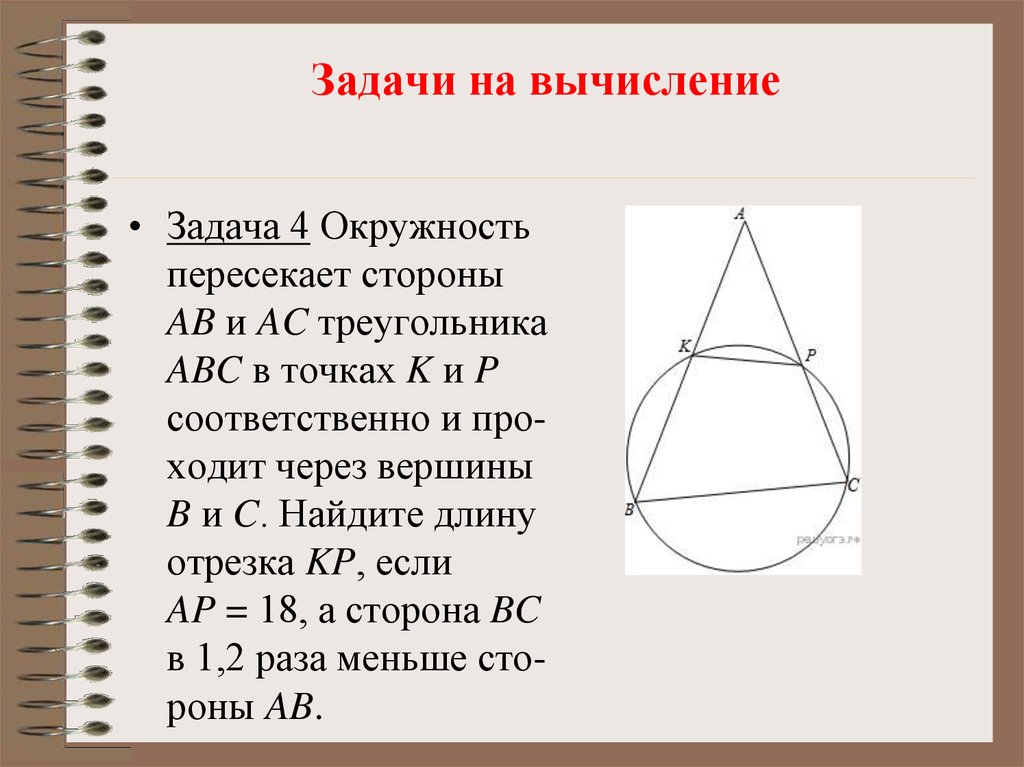
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно - №11463

В геометрии важно учитывать, что окружности могут быть связаны с различными свойствами треугольников, такими как центры тяжести и ортоцентры.

СМЕСИ И СПЛАВЫ, ПРОЦЕНТЫ ПРОСТЫМ ЯЗЫКОМ - Математика ОГЭ 2022 - Умскул
Не забудьте, что теоремы о пересечении окружности и сторон треугольников могут иметь разнообразные приложения в задачах на доказательства.

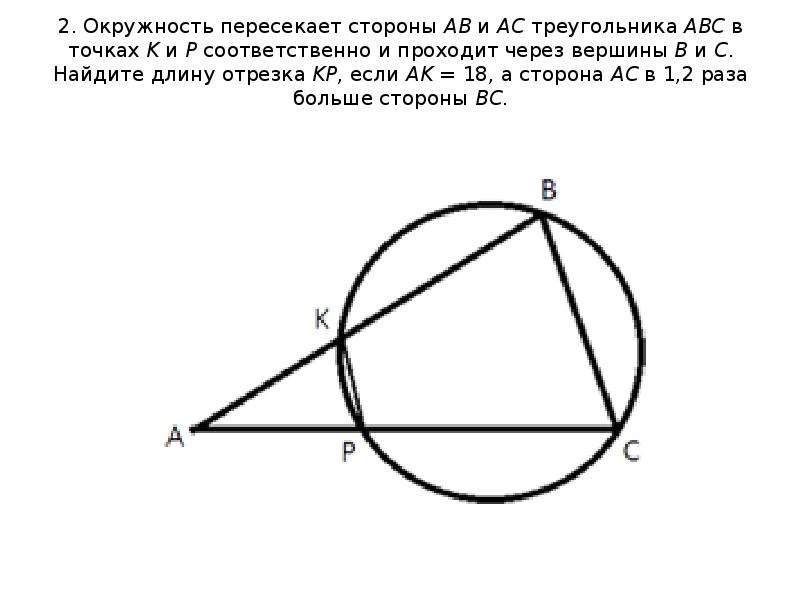
Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС

При решении задач, связанных с окружностями и треугольниками, полезно использовать симметричные и аналогичные рассуждения для упрощения вычислений.

Чтобы глубже понять взаимодействие окружности и треугольника, изучайте примеры на практике, решая задачи, которые демонстрируют реальные геометрические построения.

В некоторых случаях может быть полезно использовать методы проекций для нахождения точек пересечения окружности с прямыми, что ускоряет решение задач.

ДЕМОВЕРСИЯ ОГЭ 2025 по математике - РАЗБОР 2 ЧАСТИ ОГЭ ПО МАТЕМАТИКЕ 2025 - 99 баллов

Не забывайте про важность симметрии и взаимосвязей в треугольниках с окружностями при решении более сложных задач.


Для решения задач по окружностям и треугольникам часто используют такие понятия, как радиус, центры окружности и их отношения к сторонам треугольника, что помогает упростить анализ.

ОГЭ по математике. Вторая часть - 23-е задания