Как решить задачу на нахождение углов при условии, что один угол в 5 раз больше другого
В этой задаче вам нужно будет найти два смежных угла, зная, что один угол в 5 раз больше другого. Это типичная задача на геометрические отношения, где нужно применить свойства углов и уравнения для их нахождения.

Начните с того, что обозначьте меньший угол за x, а больший угол — за 5x.

Вариант 18, № 3. Свойство смежных углов. Пример 1

Вспомните, что сумма смежных углов всегда равна 180 градусам, то есть x + 5x = 180.

Найдите смежные углы если один из них в 5 раз больше другого

Упростите уравнение: 6x = 180, откуда x = 30.

Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.

После того, как найдете x, вы получите меньший угол — 30 градусов.
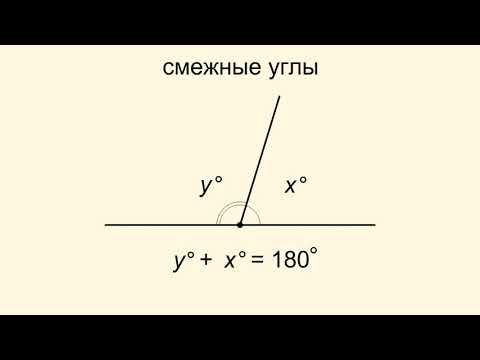
Смежные углы


Для нахождения большего угла просто умножьте x на 5: 30 * 5 = 150 градусов.
Смежные углы. 7 класс.

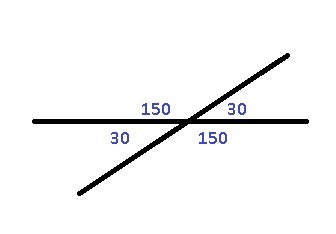
Таким образом, меньший угол равен 30 градусам, а больший угол — 150 градусам.

Проверьте решение: сумма углов должна быть 180 градусов, и это условие выполняется.

7 класс, 11 урок, Смежные и вертикальные углы
Если задача стоит в контексте геометрии, убедитесь, что углы действительно смежные, то есть общая вершина и одна сторона.

№59. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?

Используйте аналогичные методы для других задач, где углы выражаются через множители или отношения.

Геометрия 7 класс/ Найдите градусную меру большего из смежных углов, если он на 90 больше смежного
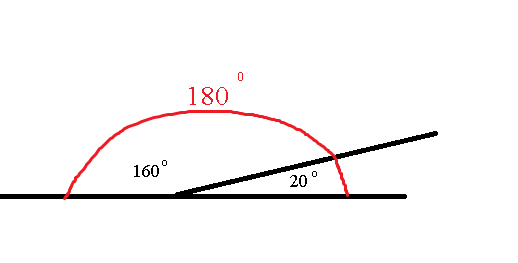
Внимательно проверяйте правильность решений и не забывайте про единицы измерения углов, они всегда должны быть в градусах.

Найдите смежные углы, если один из них в 8 раз меньше другого.
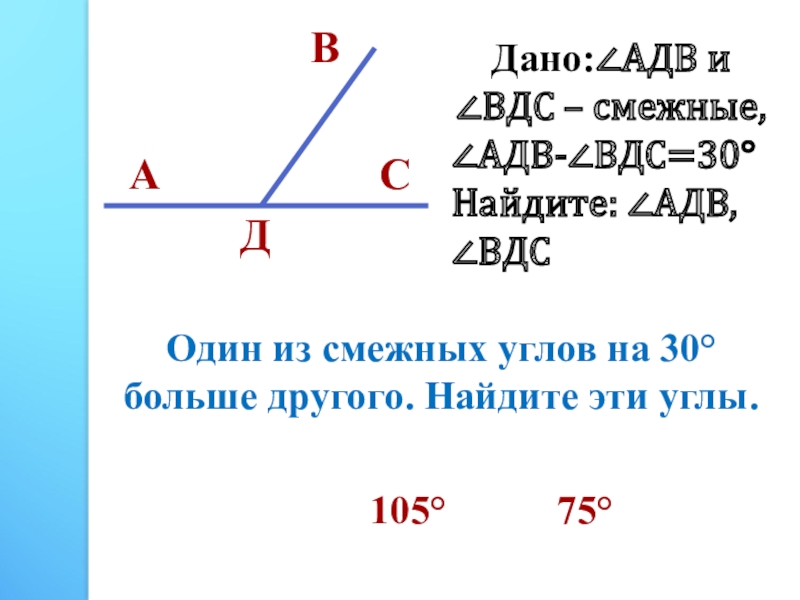
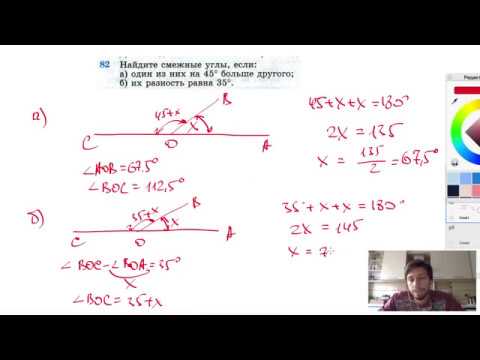
№82. Найдите смежные углы, если: а) один из них на 45° больше другого;