Алгоритм нахождения ранга матрицы через приведение к ступенчатой форме

В этой статье мы расскажем о методе нахождения ранга матрицы, используя приведение к ступенчатому виду. Это один из стандартных способов вычисления ранга, который позволяет быстро определить количество линейно независимых строк или столбцов в матрице. Приведение матрицы к ступенчатой форме позволяет легко увидеть количество ненулевых строк, что и определяет ранг.

Для начала преобразуйте матрицу в ступенчатую форму с помощью элементарных преобразований строк.

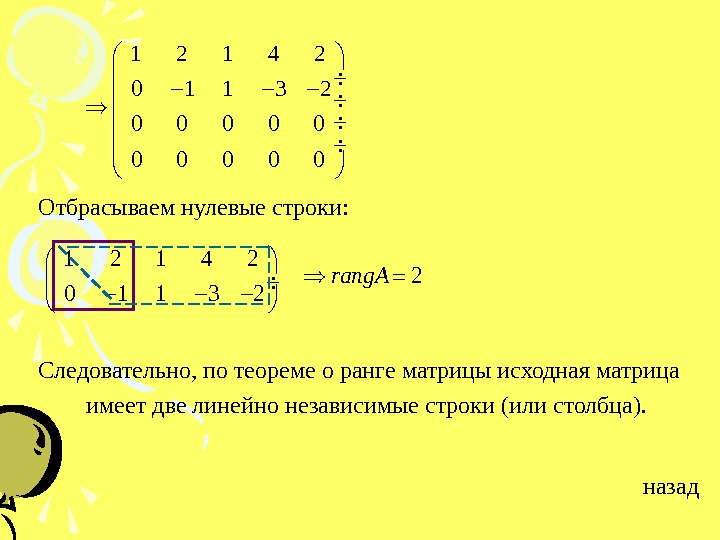
При выполнении преобразований следите за тем, чтобы не изменить линейную зависимость строк или столбцов.

После получения ступенчатой формы определите количество ненулевых строк — это и будет ранг матрицы.

Если после приведения матрицы к ступенчатому виду осталась хотя бы одна строка, состоящая из нулей, она не влияет на ранг.

Используйте для приведения к ступенчатой форме операции перестановки строк, умножение строки на ненулевое число и сложение строк.

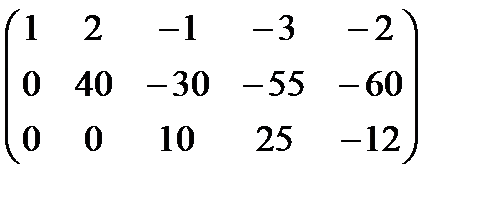
Не забывайте, что строки, содержащие только нули, всегда исключаются из расчета ранга.

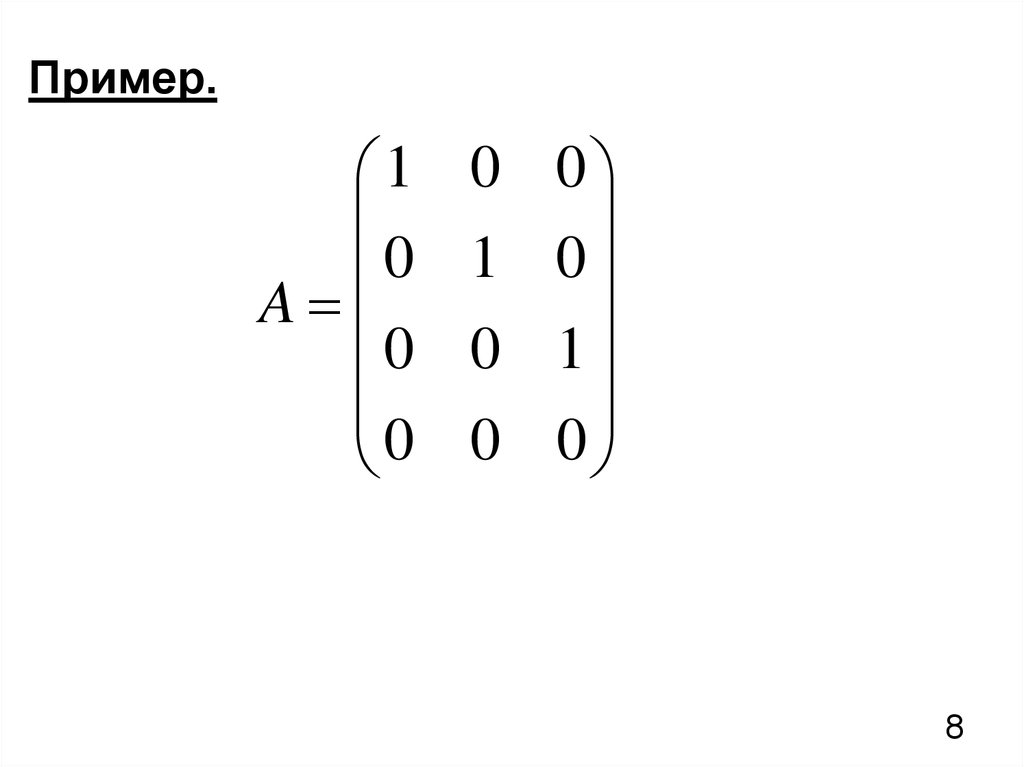
Если при приведении матрицы к ступенчатой форме вы получаете строку, содержащую только нули, уменьшите размер матрицы на одну строку.

Часто удобно использовать алгоритм Гаусса для нахождения ступенчатой формы, так как он включает четкие шаги для упрощения матрицы.

Для матриц больших размеров рекомендуется использовать программное обеспечение, которое автоматически приведет матрицу к ступенчатому виду и вычислит ранг.

Важно помнить, что ранг матрицы не зависит от выбора строк и столбцов, если при этом не происходит изменения линейной зависимости между ними.