Медианы треугольника ABC: теоремы, вычисления и примеры их применения
На этой странице собраны полезные советы и визуальные материалы, которые помогут вам разобраться в вычислениях медиан треугольника ABC. Мы рассмотрим, как найти медианы, как они пересекаются в центре тяжести и какие их особенности имеют важное значение при решении геометрических задач.
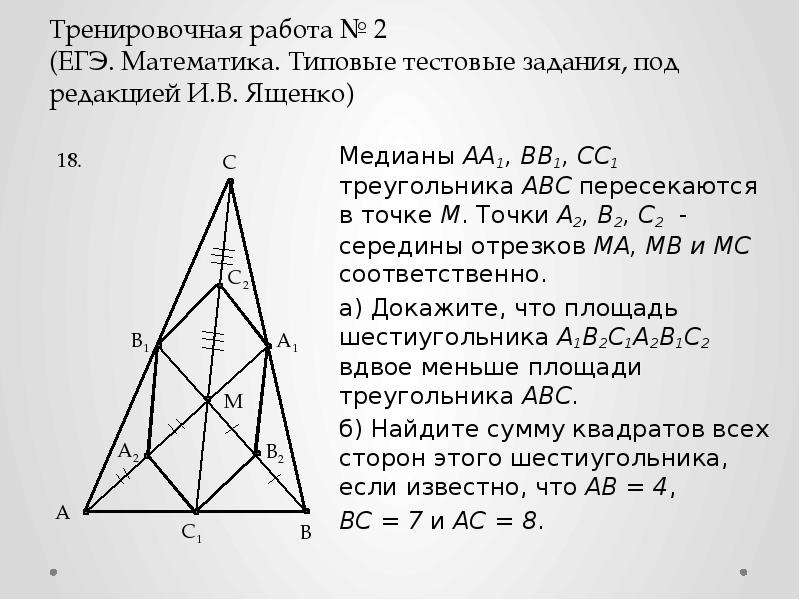

При расчете медиан важно помнить, что они соединяют вершины треугольника с серединой противоположных сторон.
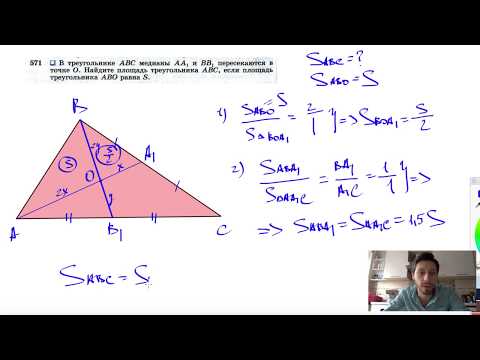
№571. В треугольнике ABC медианы АА1 и ВВ1 пересекаются в точке О. Найдите площадь
Для того чтобы найти длину медианы, можно использовать формулу, зависящую от длин сторон треугольника, которая также включает полупериметр.

Реакция на результаты ЕГЭ 2022 по русскому языку

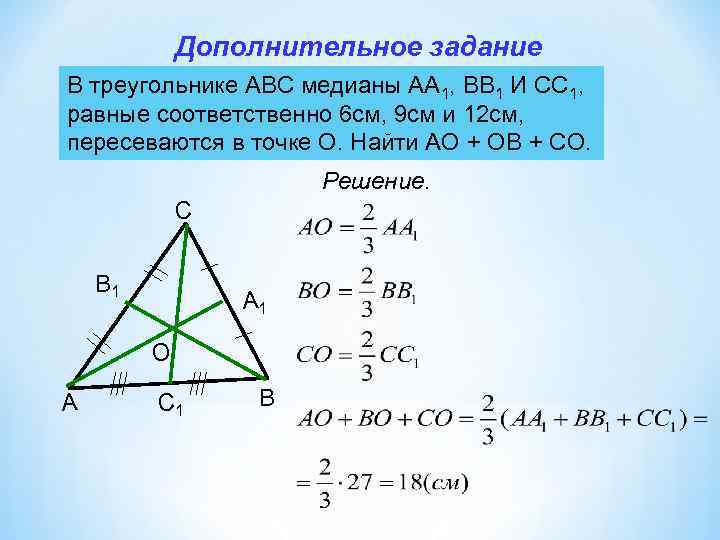
Пересечение всех медиан треугольника всегда происходит в одной точке, называемой центром тяжести треугольника.

Геометрия Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB

Если треугольник равнобедренный, то медианы, проведенные из двух равных углов, будут равны и пересекаться на одной оси симметрии.

Длина медианы треугольника

Медианы делятся точкой пересечения в отношении 2:1, где большая часть приходится на часть от вершины до центра тяжести.

ABC АНАЛИЗ для маркетплейсов. Инструкция.

При решении задач на медианы важно учитывать, что они могут быть использованы для нахождения площади треугольника через формулу Герона.
Для вычисления длины медианы также можно использовать теорему о медиане, которая поможет найти ее по трем сторонам треугольника.

При проведении медианы важно точно определить середины сторон, так как ошибочное определение точки может привести к неверным расчетам.
Медианы играют важную роль в построении более сложных геометрических фигур, таких как многоугольники и многогранники.

Знание свойств медиан поможет вам решать более сложные задачи, например, вычислять центры масс для различных геометрических объектов.