Роль линейной проекции в представлении трехмерных объектов на плоскости
Линейная проекция — это метод отображения трехмерных объектов на двумерной поверхности, который используется в различных областях, от архитектуры до компьютерной графики. Это мощный инструмент для создания чертежей и иллюстраций, а также для понимания пространственных отношений между объектами. В этой статье мы рассмотрим, как работает линейная проекция и какие полезные советы помогут вам эффективно использовать этот метод в работе.


Для точного представления объектов в линейной проекции важно правильно определить точки зрения, чтобы избежать искажений.

Проецирование прямой общего положения
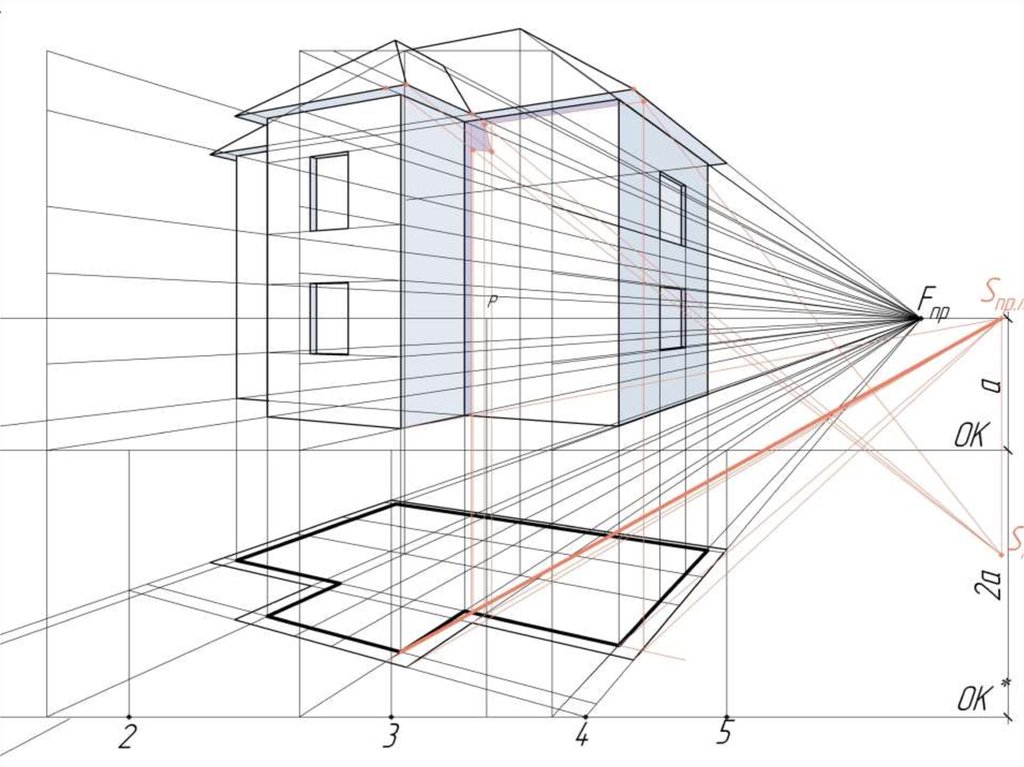
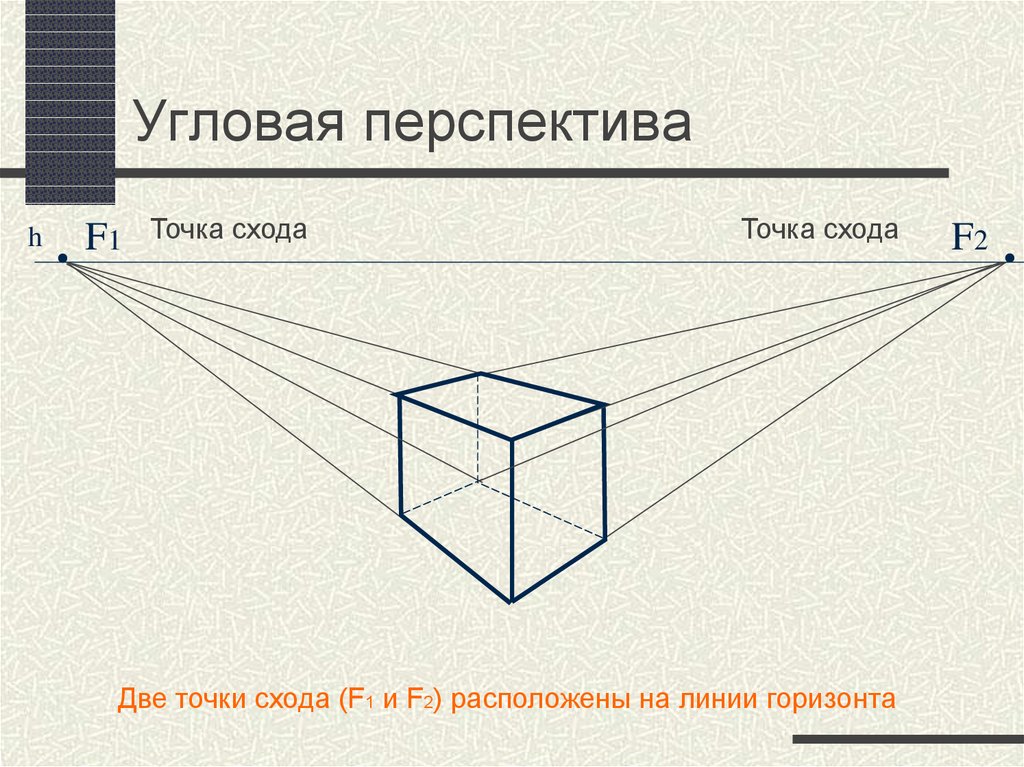
При создании проекций важно соблюдать пропорции, чтобы объекты выглядели реалистично и сохранили свою форму.

Видеоурок \


Использование ортогональной проекции помогает избежать перспективных искажений, что особенно полезно для технических чертежей.

Аналитическая геометрия, 1 урок, Векторы в пространстве
При работе с линейной проекцией важно помнить, что линии, параллельные друг другу, в проекции не всегда остаются параллельными.

Частное положение точек. Точки принадлежащие к плоскостям проекции.
Для улучшения восприятия проекций можно использовать разные типы проекций: аксонометрические, перспективные и ортогональные, в зависимости от задачи.

Линейная алгебра. Векторы и операции над векторами.

Разные виды проекций подходят для разных целей: например, в архитектуре часто применяют планы и фасады, а в инженерии — виды с пересечением элементов.
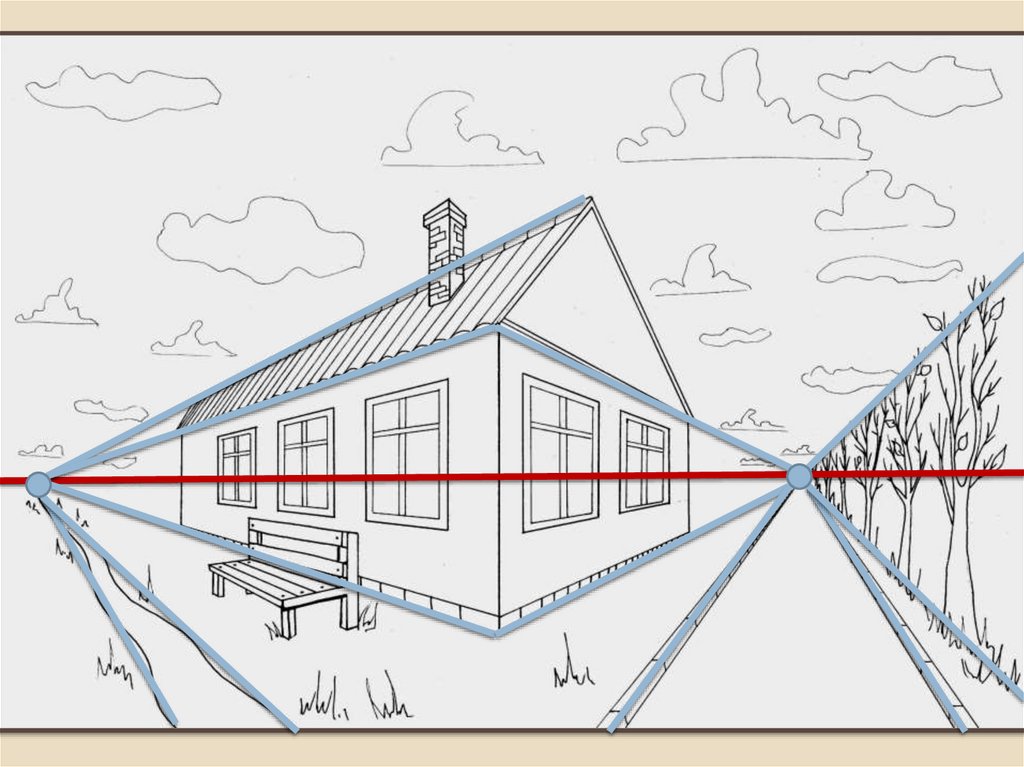
Линейная проекция особенно полезна при работе с абстрактными и геометрическими формами, где важна точность и детализированность.

За халявой переходи в шапку профиля #огэ #онлайншкола #математика #егэ

Используйте программы для создания чертежей и 3D-моделей, чтобы ускорить процесс построения линейных проекций и снизить вероятность ошибок.

Семинар по линейной алгебре. Сумма и пересечение подпространств. Прямая сумма, проекция.

A.7.3 Проекции векторов. А вот и датасайнс!
Не забывайте про масштабирование — при создании проекций важно учитывать размеры объектов в реальном мире, чтобы они корректно отображались на плоскости.

Для лучшего понимания принципов линейной проекции полезно изучать примеры и практиковаться на простых фигурах, прежде чем переходить к более сложным объектам.
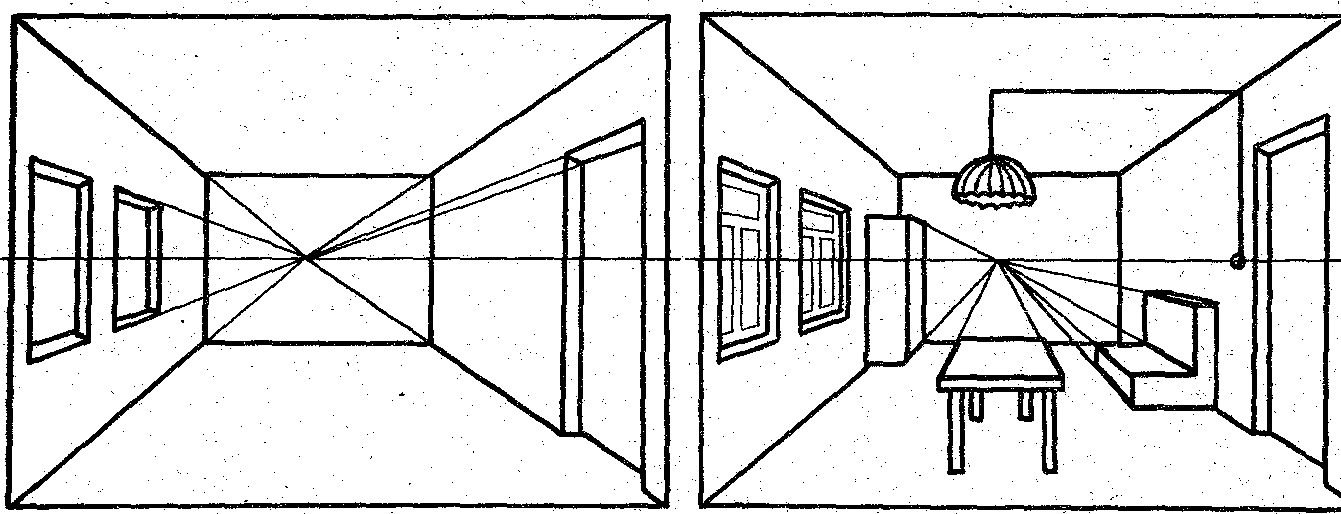
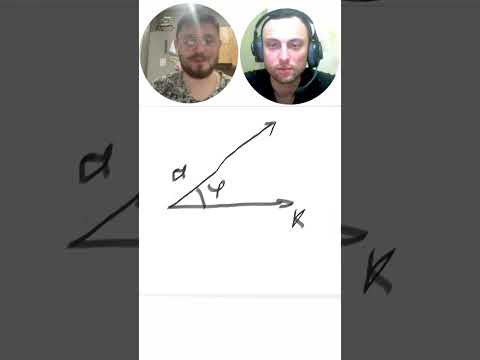
Проекция вектора на ось: Линейная алгебра для Data Science #datascience #machinelearning