Пошаговое руководство по переводу чисел из 16-й системы счисления
Перевод чисел из шестнадцатеричной системы счисления может показаться сложной задачей, но при использовании правильных методов это становится достаточно простым процессом. В этой подборке вы найдете советы и рекомендации, которые помогут вам освоить этот процесс с нуля и избежать распространенных ошибок.



Для перевода числа из 16-й системы счисления в десятичную начните с того, что запишите все цифры шестнадцатеричного числа и умножьте каждую из них на степень 16, соответствующую её позиции.

Перевод(из 2 в 16) из двоичной в шестнадцатеричную и likerkacinema.ruй и лёгкий. Системы счисления.


Каждая цифра в шестнадцатеричном числе имеет свою позицию, начиная с самой правой (единицы) и двигаясь влево: 16^0, 16^1, 16^2 и так далее.

Перевод из 16 в 8 систему счисления

Помните, что в шестнадцатеричной системе цифры от 0 до 9 представляют собой обычные цифры, а буквы A-F соответствуют числам от 10 до 15.

Перевод чисел в восьмеричную и шестнадцатеричную систему счисления и обратно


Чтобы перевести букву в число, используйте следующую таблицу: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

Перевод числа в двоичную систему за два шага!!!

После того как вы умножили цифры на соответствующие степени 16, сложите все полученные значения для получения итогового десятичного числа.

Шестнадцатеричная система счисления

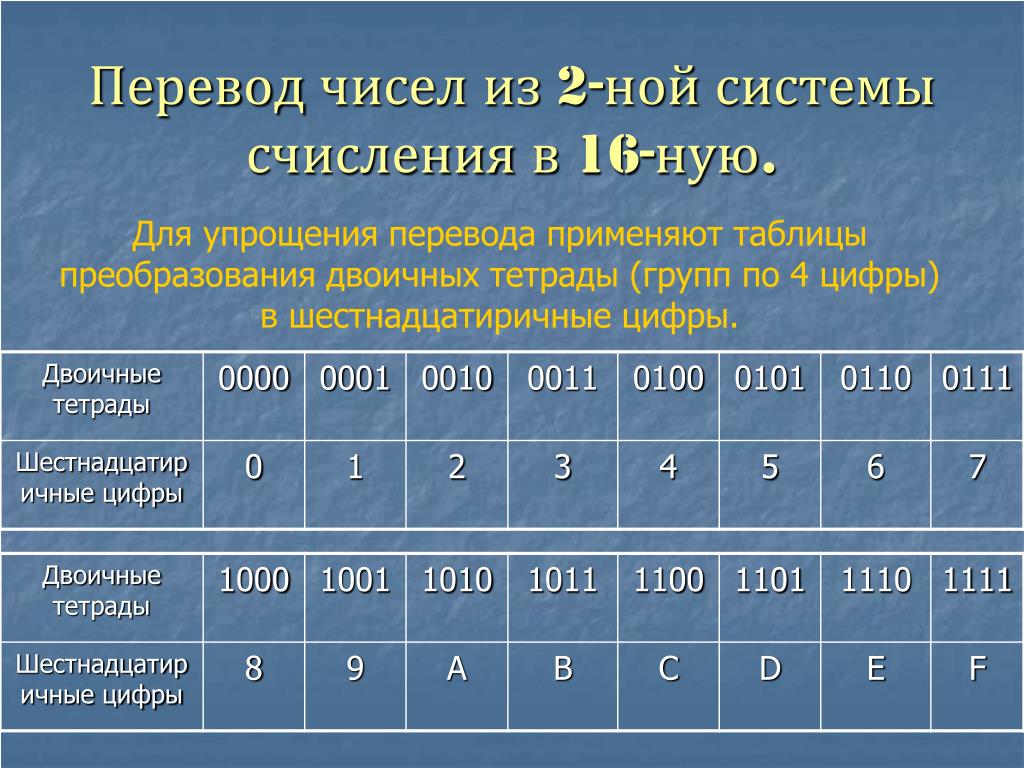
Не забудьте, что для чисел, записанных в нижнем регистре, нужно учитывать одинаковое значение для заглавных и строчных букв в шестнадцатеричной системе.
Используйте калькуляторы или онлайн-инструменты для проверки правильности перевода, особенно если вам нужно часто работать с шестнадцатеричными числами.

Андрей Фурсов: Мы ведём битву, к которой готовился Сталин!


Для удобства можно записать число в виде разложения: например, 2F3 в 16-й системе — это (2 * 16^2) + (15 * 16^1) + (3 * 16^0).
Внимательно следите за точностью в вычислениях, особенно при работе с большими числами, чтобы избежать ошибок в разрядах.
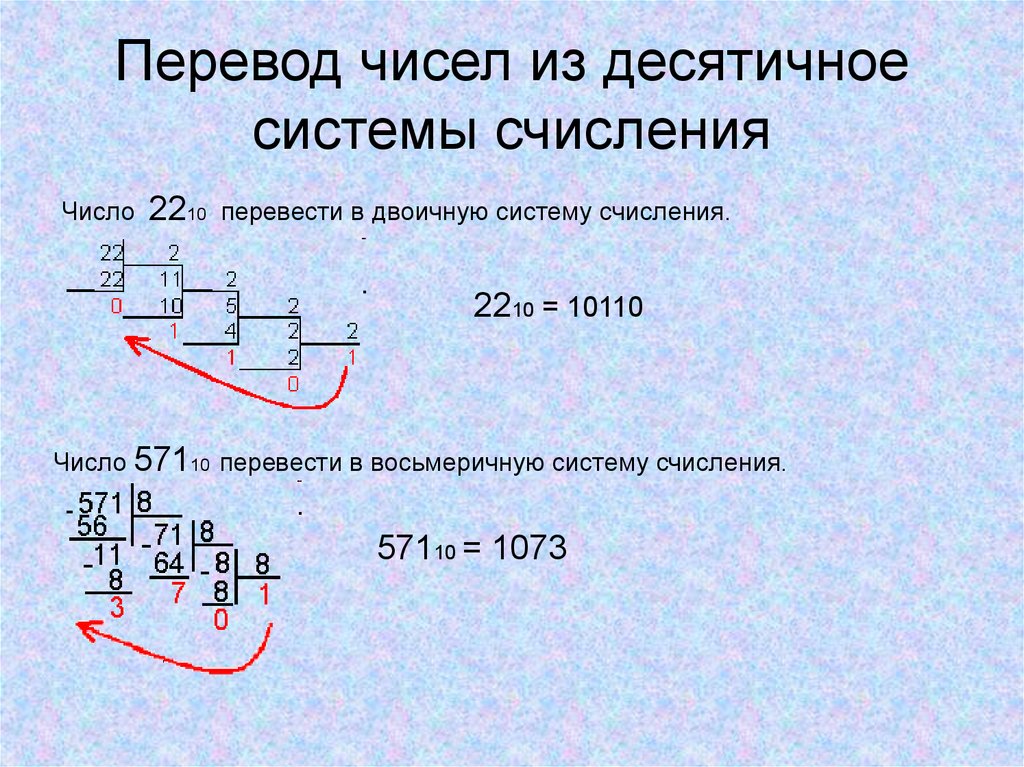
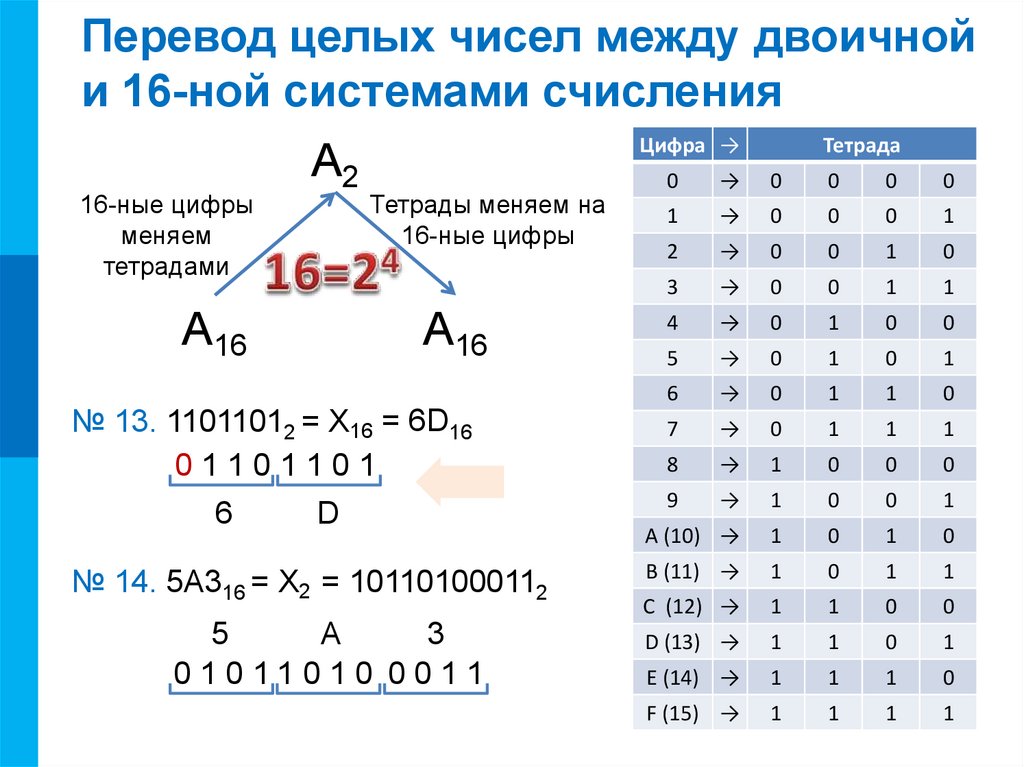
Не забывайте о возможных сложностях с преобразованием при использовании разных систем счисления (например, двоичной или восьмеричной), так как алгоритм будет немного отличаться.