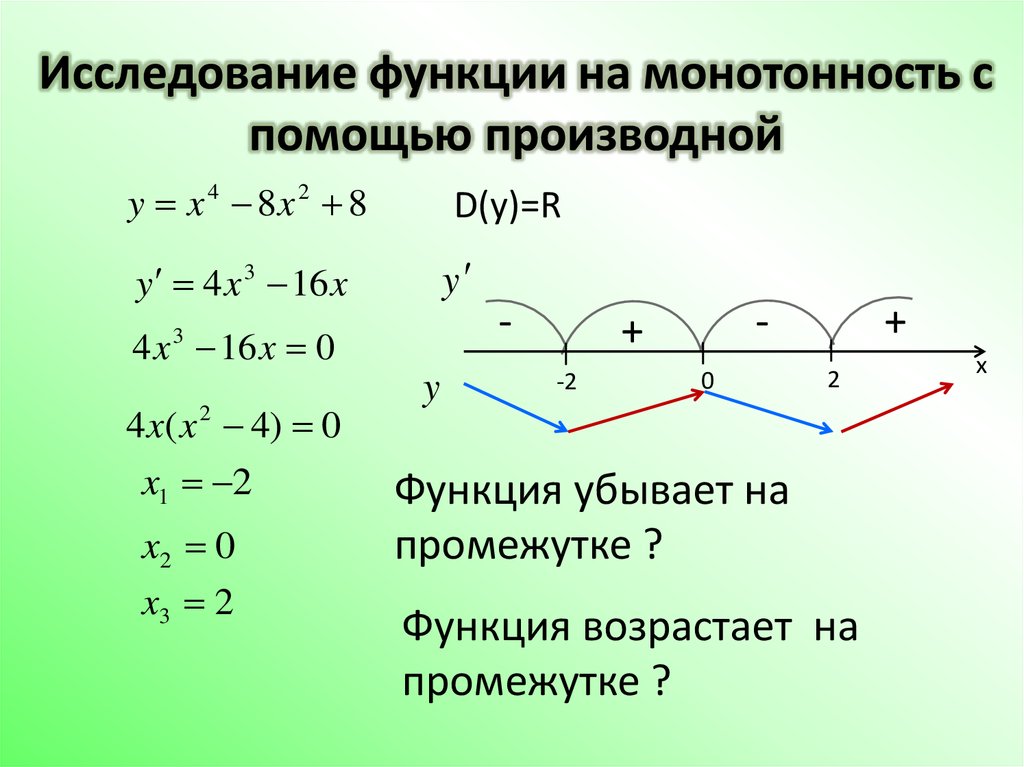
Монотонность функции: исследование через производную легко и быстро
На этой странице вы найдете полезные советы и подробное описание процесса исследования функции на монотонность с использованием производной, а также подборку наглядных примеров и фотографий для лучшего понимания темы.


Начните с нахождения производной функции, это ключевой шаг в анализе её монотонности.
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.
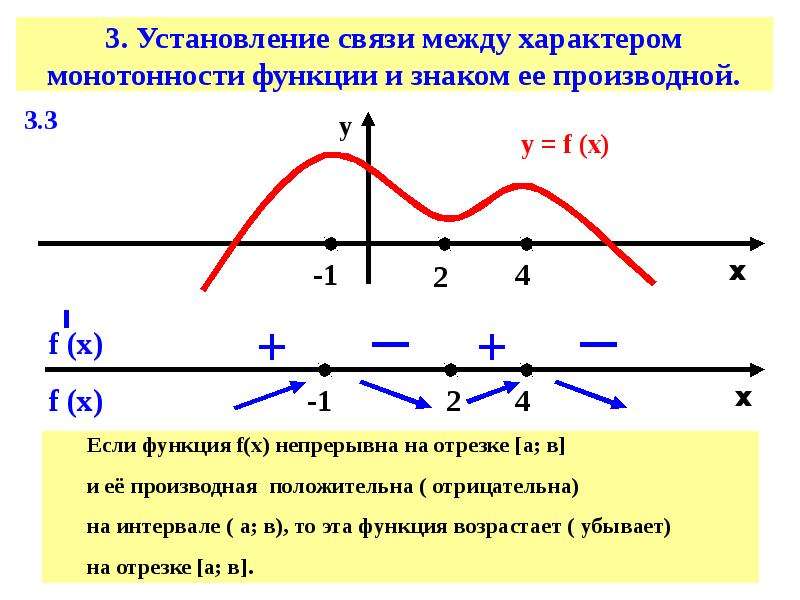

Определите, где производная равна нулю или не существует, чтобы найти критические точки функции.
Исследование функции на монотонность с применением производной
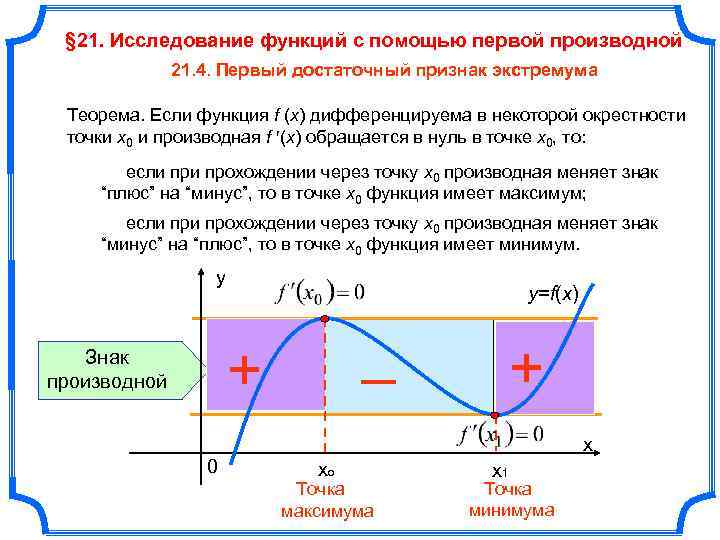
Разделите область определения функции на интервалы, используя критические точки.
10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумы
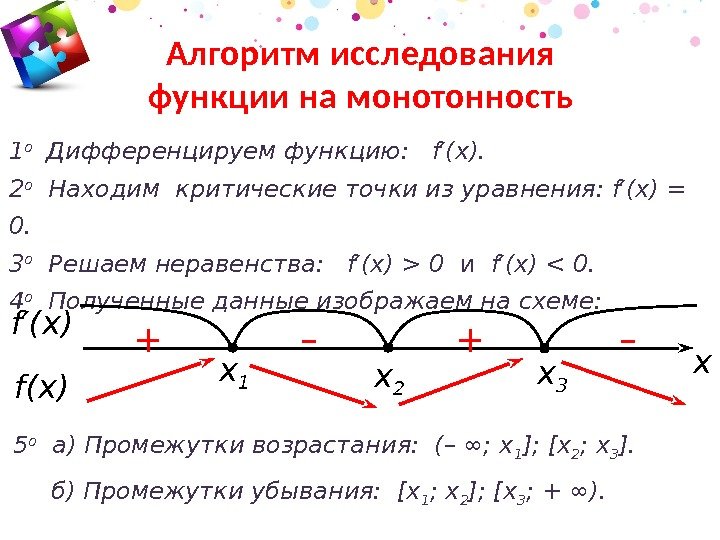

На каждом из полученных интервалов определите знак производной, подставляя значения в её выражение.

Математический анализ, 12 урок, Монотонность и экстремумы функции
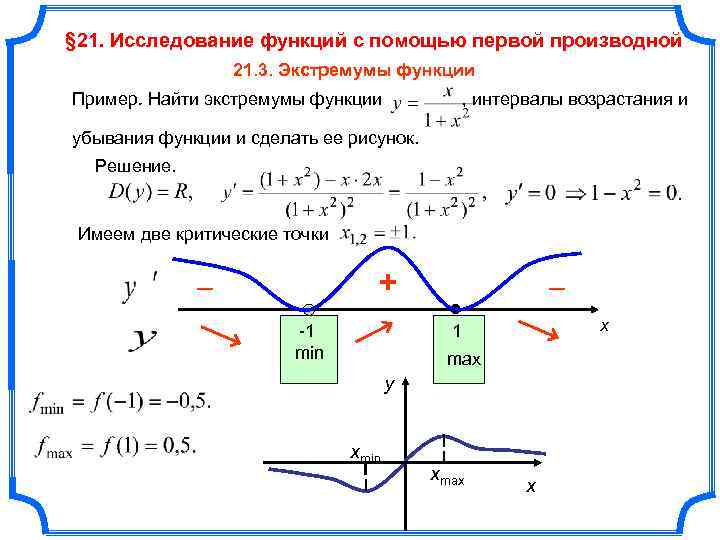
Если производная положительна на интервале, функция возрастает; если отрицательна — убывает.

Исследование функции на монотонность.


Постройте схему, которая наглядно покажет интервалы возрастания и убывания функции.
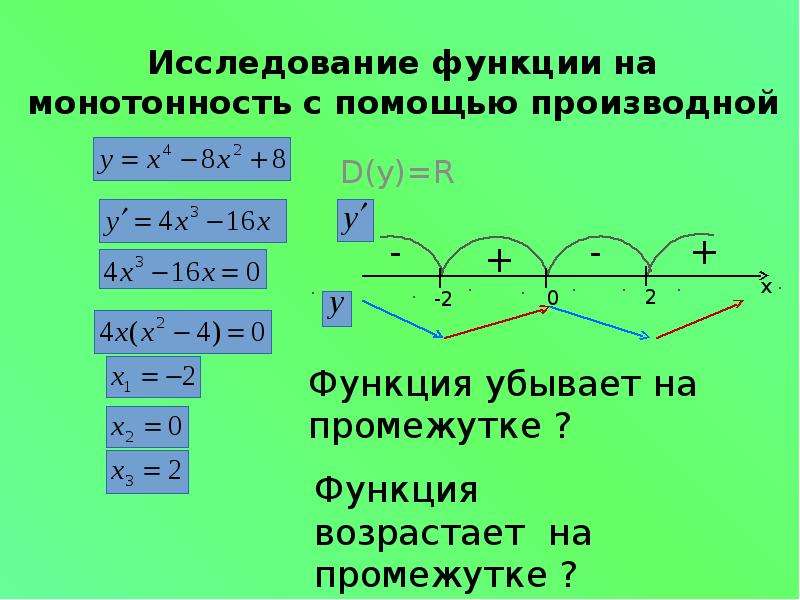
Обратите внимание на особенности поведения функции в критических точках, таких как максимумы, минимумы и точки перегиба.

Алгебра 10 класс: Применение производной для исследования функции на монотонность и экстремумы

Используйте графический метод для проверки правильности анализа — построение графика функции помогает визуализировать её монотонность.

Телеуроки. Марина Кликунене. «Применение производной в исследовании функций на монотонность»

Исследование функций с помощью производной. Практическая часть. 10 класс.

Применяйте правило анализа монотонности для более сложных функций, включая логарифмические, экспоненциальные и тригонометрические.
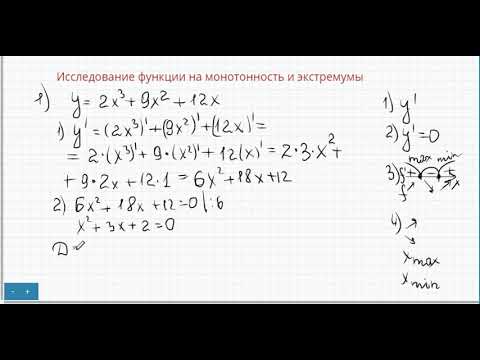
Исследование функции на монотонность и экстремумы


Практикуйтесь на простых функциях, чтобы закрепить навык анализа их монотонности с помощью производной.