Хорды окружности: определения, свойства и практические примеры
На этой странице вы найдёте подробное объяснение понятия хорды окружности, её свойства, полезные советы и фотографии для лучшего понимания темы.
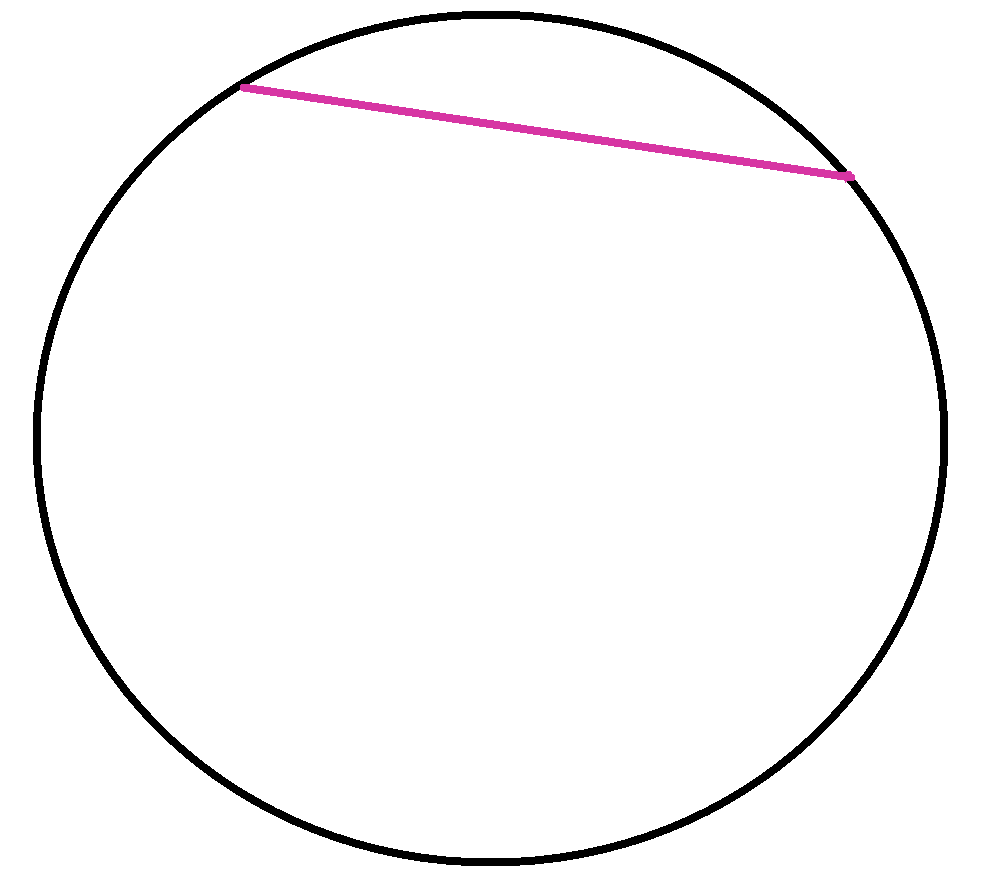

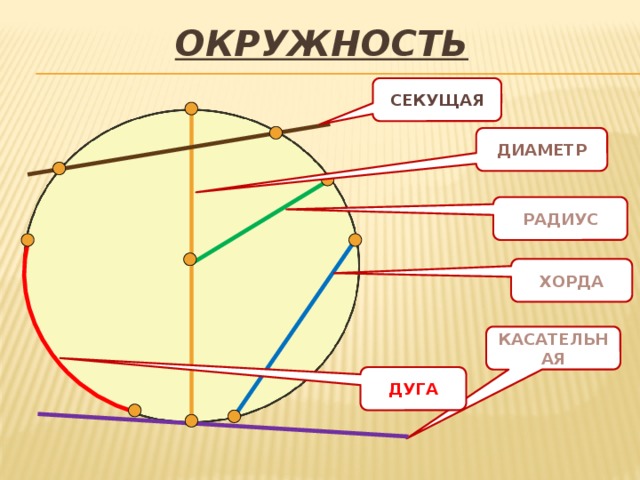
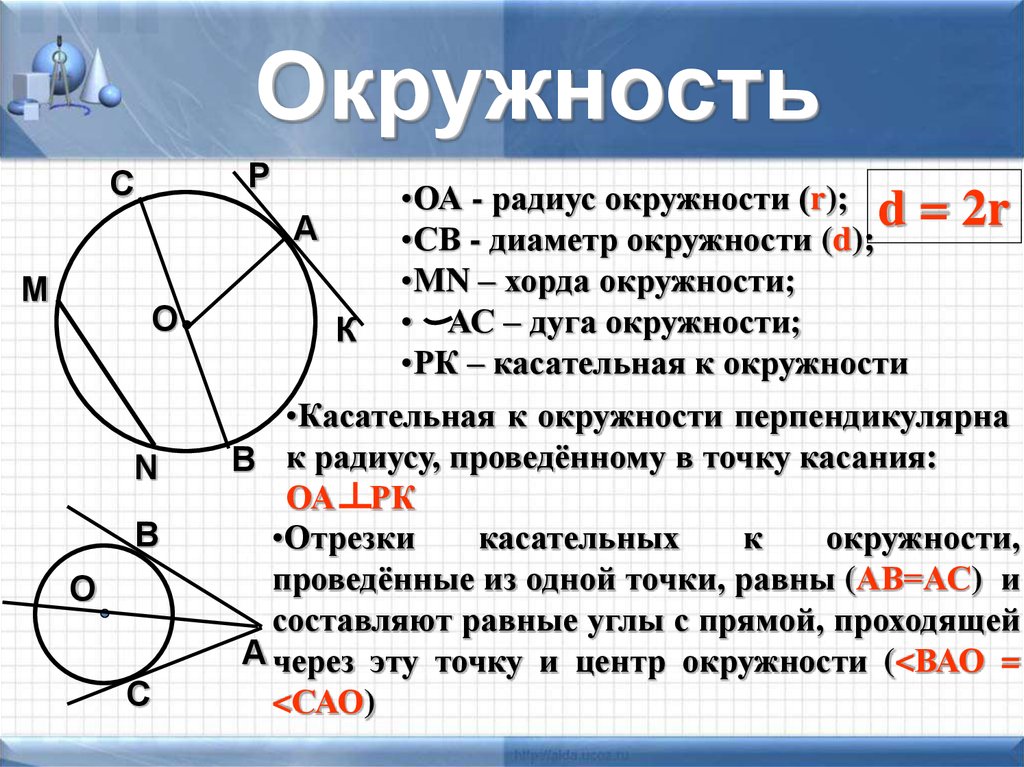
Хорда – это отрезок, соединяющий две точки на окружности. Всегда проверяйте, чтобы точки действительно принадлежали окружности.

Всё про углы в окружности. Геометрия - Математика
Длина хорды зависит от угла между радиусами, проходящими через её концы. Используйте формулы для расчётов.

Окружность, диаметр, хорда геометрия 7 класс
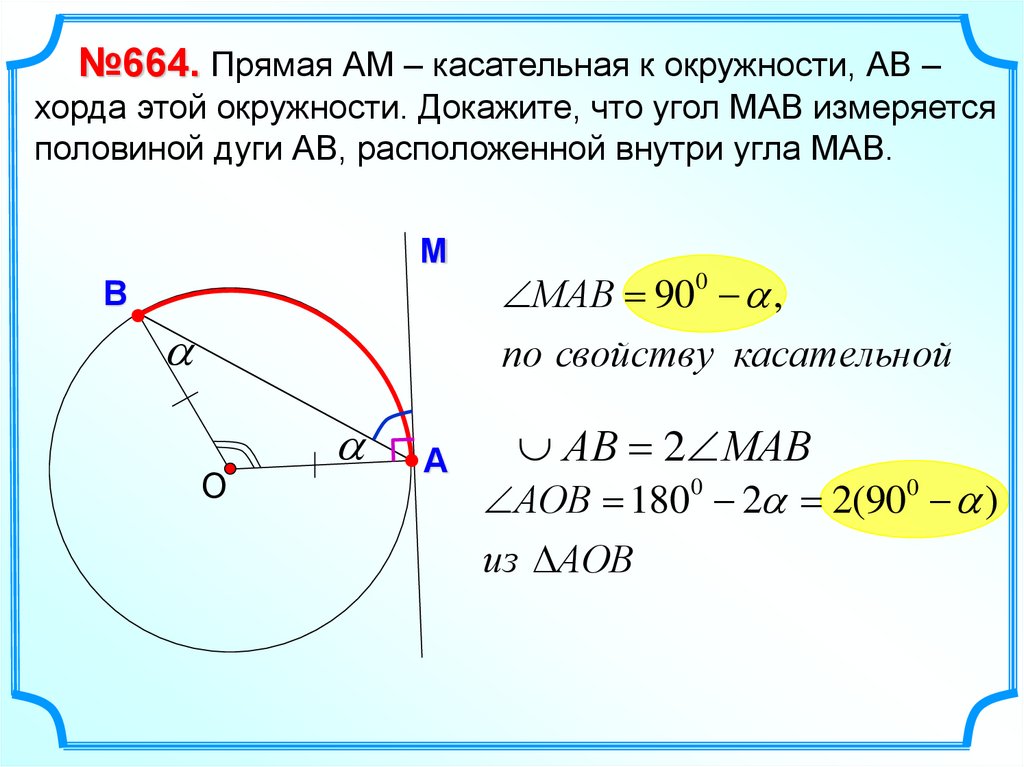
Если хорда проходит через центр окружности, она является диаметром и имеет максимальную длину.

Class 9 Maths - Chapter 9 - Circles - Theorem 9.4 - NCERT

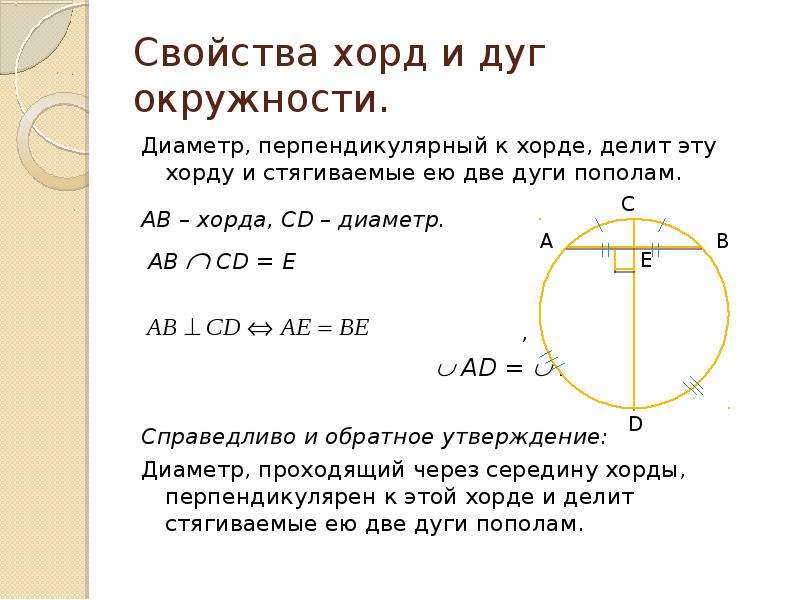
Для нахождения длины хорды можно использовать формулу: L=2Rsin(θ/2)L = 2R /sin(/theta / 2)L=2Rsin(θ/2), где RRR – радиус окружности, θ/thetaθ – угол между радиусами.
Окружнось. Зависимость длины хорды, от длины дуги.
Для построения хорды используйте циркуль и линейку, чтобы получить максимально точные результаты.

Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)
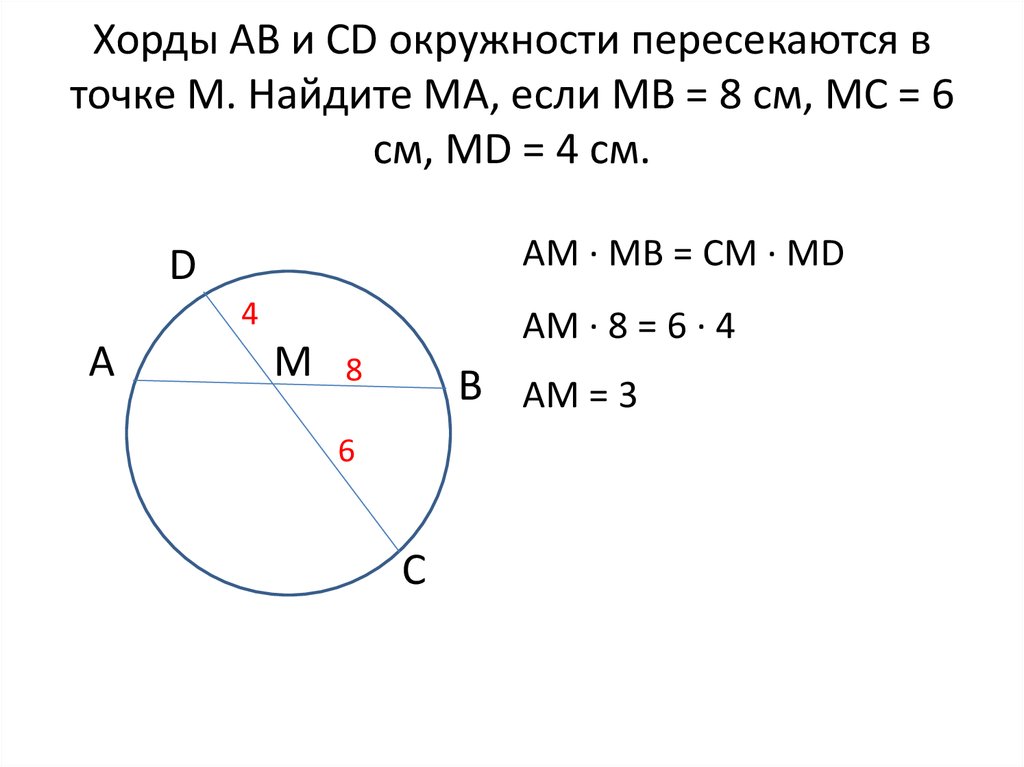

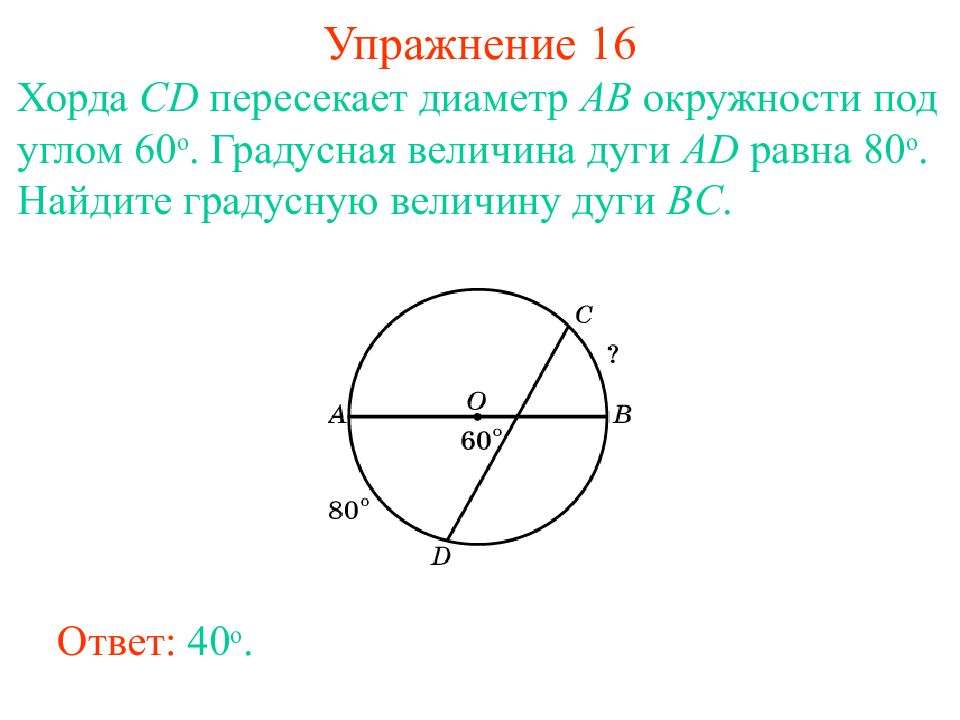
В задачах с хордой полезно знать, как найти расстояние от центра окружности до хорды. Это поможет проверить ваши расчёты.

Окружность. Длина хорды. Теорема синусов.
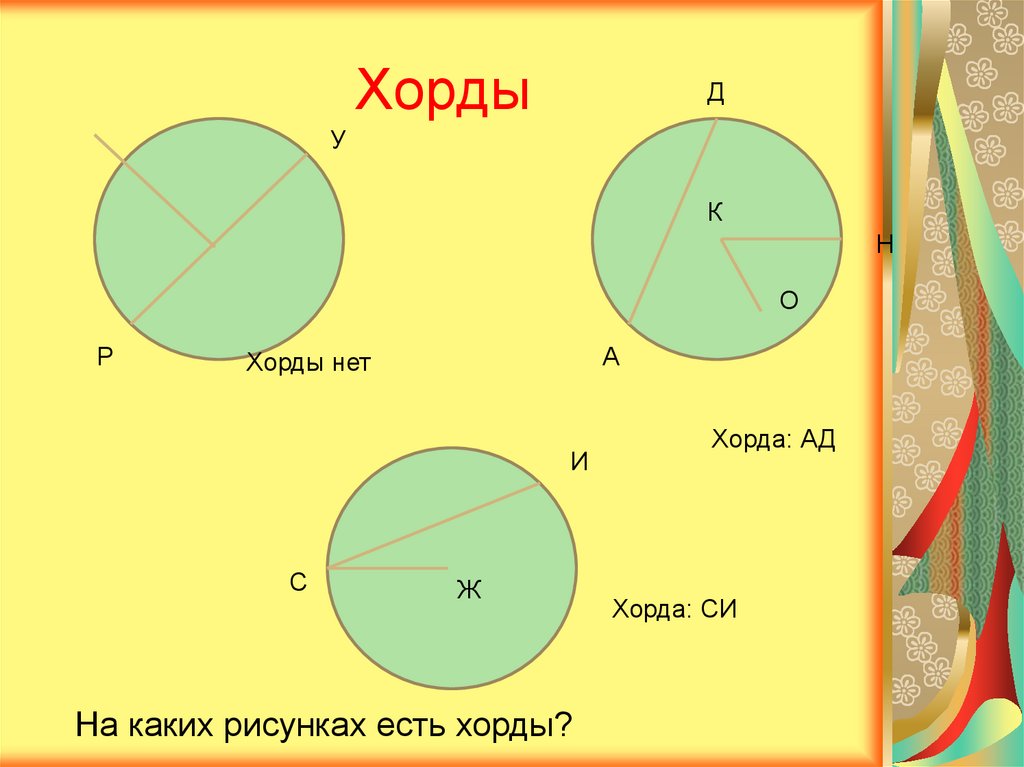
Обратите внимание, что все хорды, находящиеся на одинаковом расстоянии от центра, равны по длине.

Хорды могут помочь найти площадь сегмента окружности. Используйте интегралы или геометрические формулы.

Геометрия Хорда окружности равна 10 см. Через один конец хорды проведена касательная к окружности
Знание свойств хорд полезно для решения задач на экзаменах по геометрии, поэтому уделите этому особое внимание.
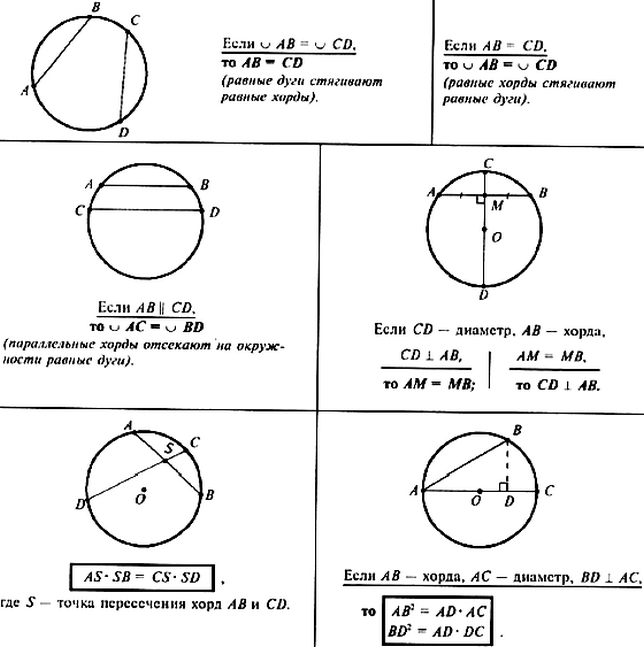
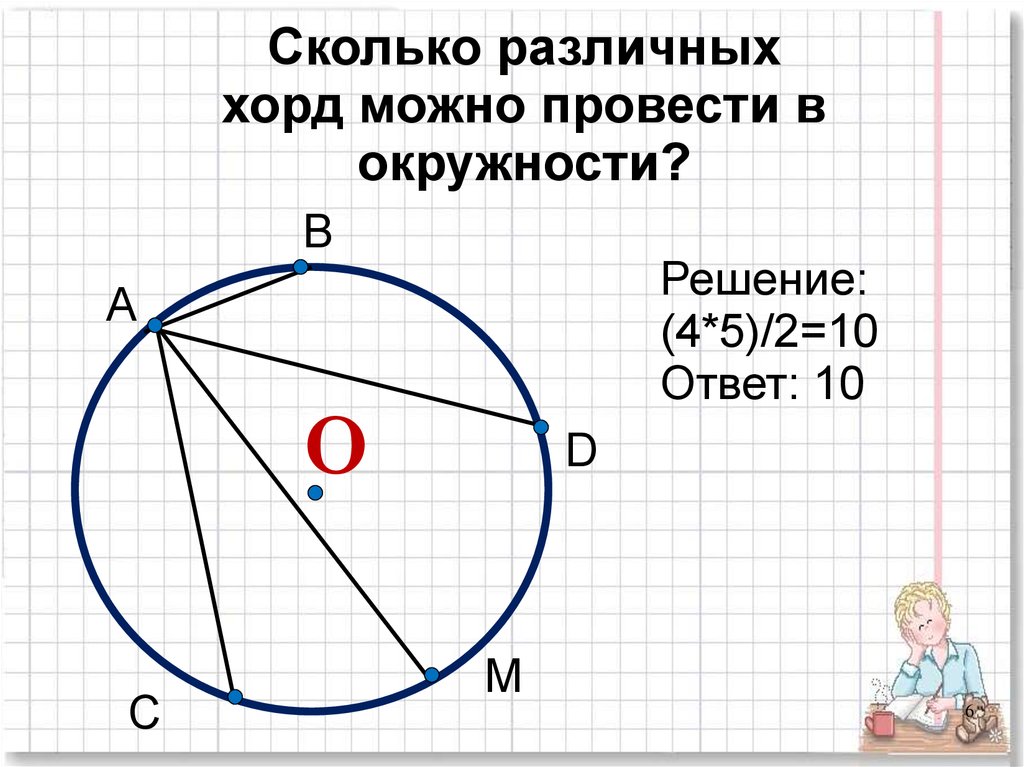
Используйте графические приложения или программы, такие как GeoGebra, для визуализации задач с хордой окружности.
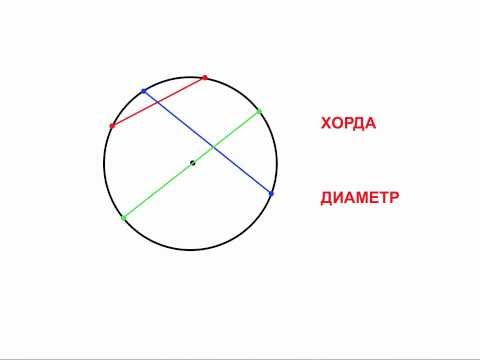
Окружности - хорда, диаметр