Основные принципы и советы по созданию графов без кратных рёбер
Графы без кратных рёбер представляют собой важную категорию в теории графов, где между любыми двумя вершинами существует не более одного ребра. Эта концепция применяется во множестве задач, включая маршрутизацию, сетевые структуры и оптимизацию. Важно правильно подходить к построению таких графов, чтобы избежать ненужных повторов и ошибок в расчетах. В этой статье представлены полезные советы по созданию и анализу графов без кратных рёбер.
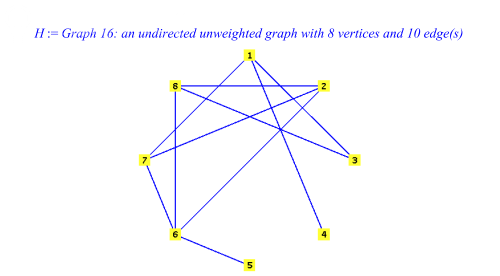

При построении графа убедитесь, что для каждой пары вершин существует не более одного ребра. Это важно для сохранения структуры графа и предотвращения избыточности.

GIT-метрики, выявляющие неэффективных коллег - Алексей Бахирев
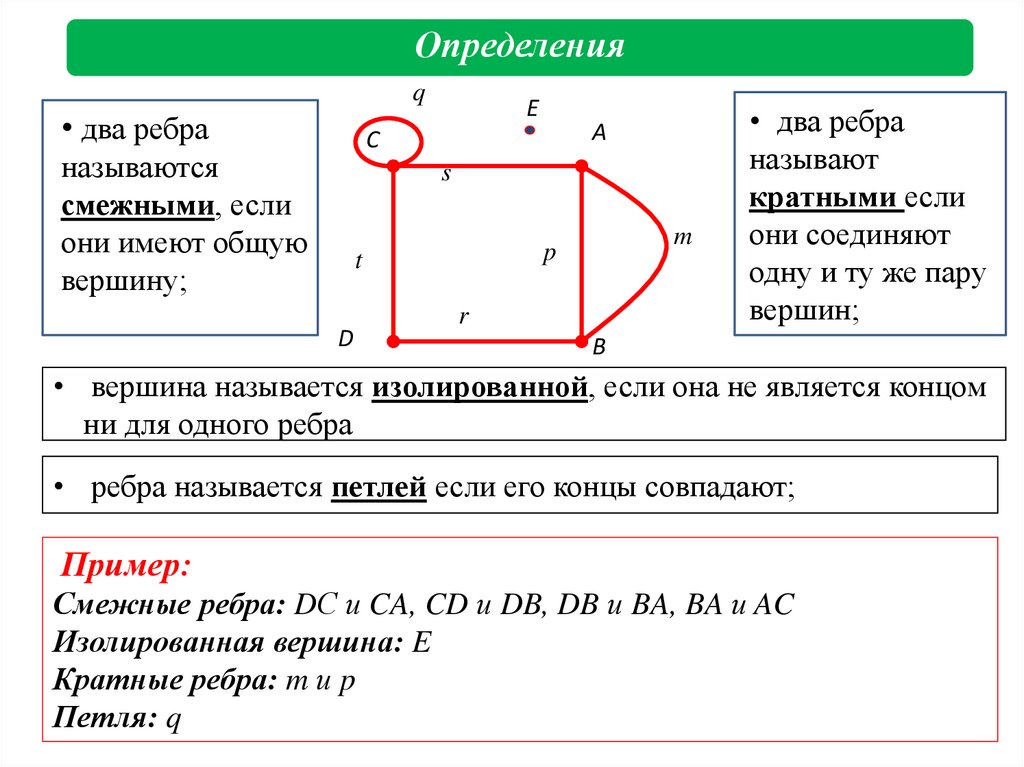

Для автоматической проверки наличия кратных рёбер используйте алгоритмы, которые могут быстро и эффективно искать повторяющиеся рёбра в графе.

Элементы теории графов. Типовые задачи.
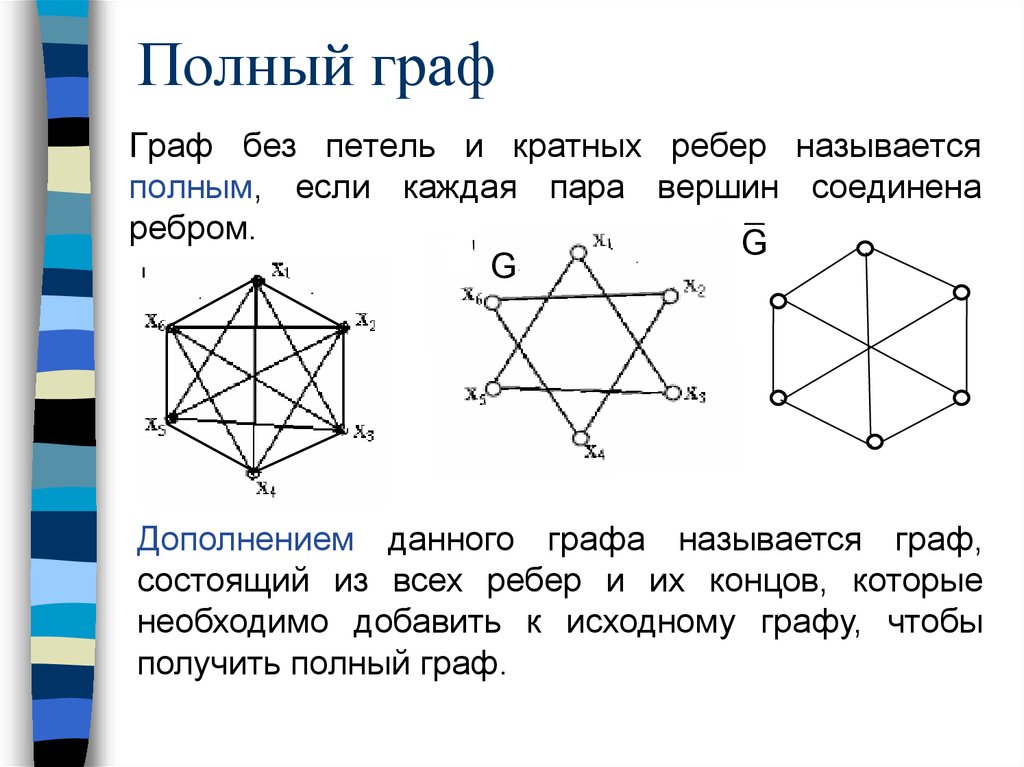
Визуализируйте графы с помощью специализированных инструментов, чтобы наглядно увидеть возможные кратные рёбра и их влияние на структуру графа.
Информатика - Урок 2 - Введение в графы, соотношение числа вершин и рёбер в графе.
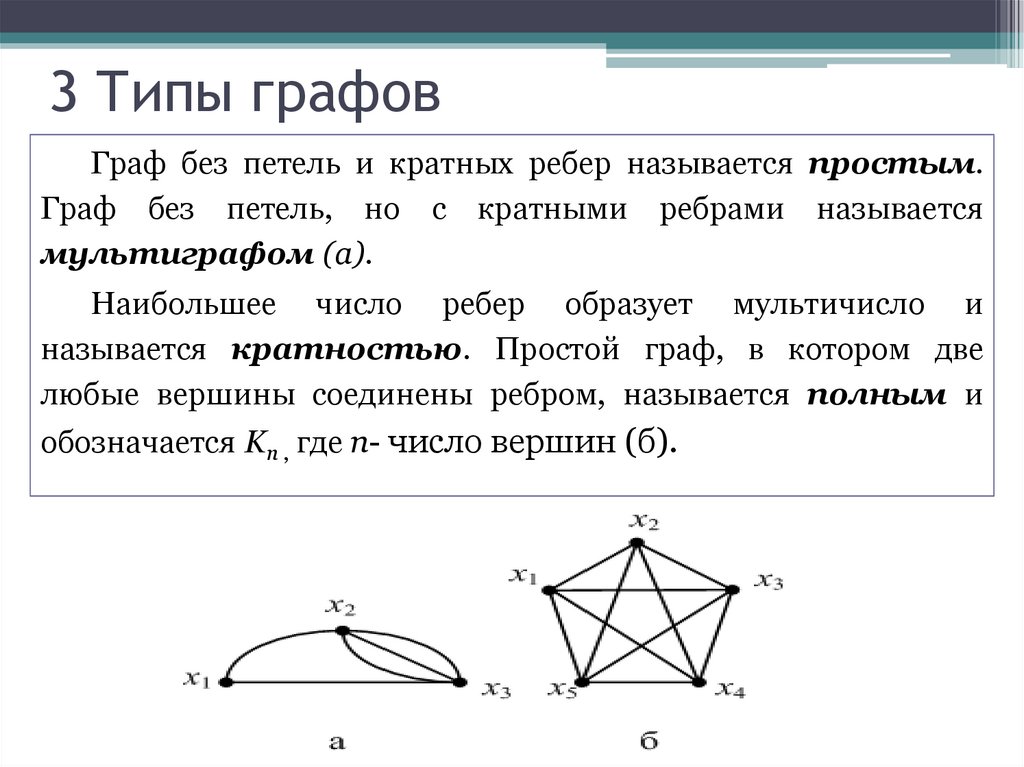
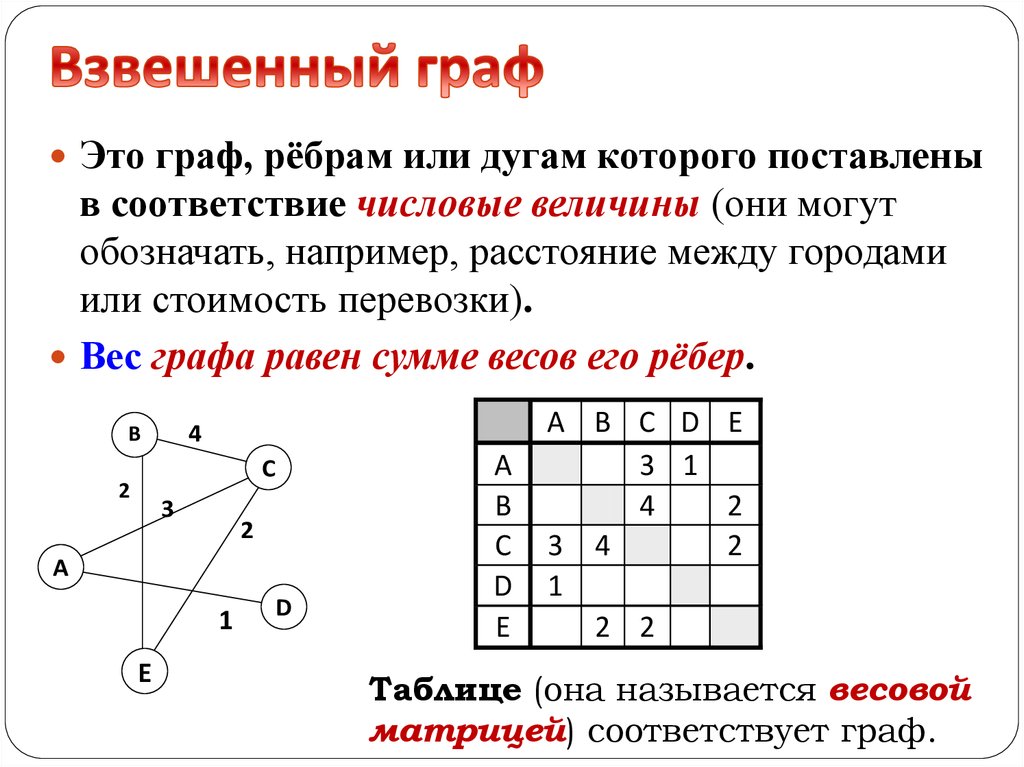
Используйте подходящие модели данных, такие как списки смежности или матрицы смежности, которые позволяют удобно управлять связями между вершинами и избежать избыточных рёбер.

Основы теории графов. Связный граф. Дерево. Путь. Петля. Степень вершины. Цикл. 6 лекция
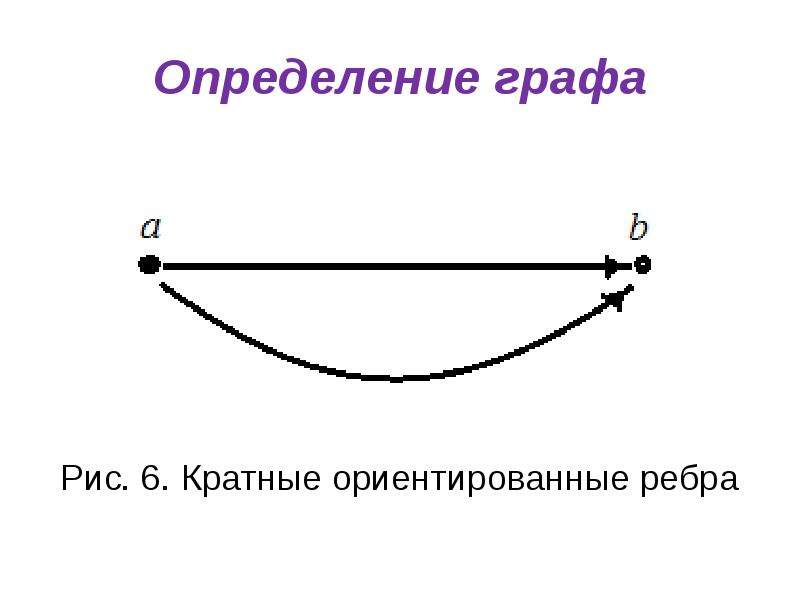
Обратите внимание на то, что графы без кратных рёбер могут быть полезны для решения задач оптимизации, где важно минимизировать количество связей между объектами.

Лекция 2 (Продолжающая группа) Графы (Уровень 4)

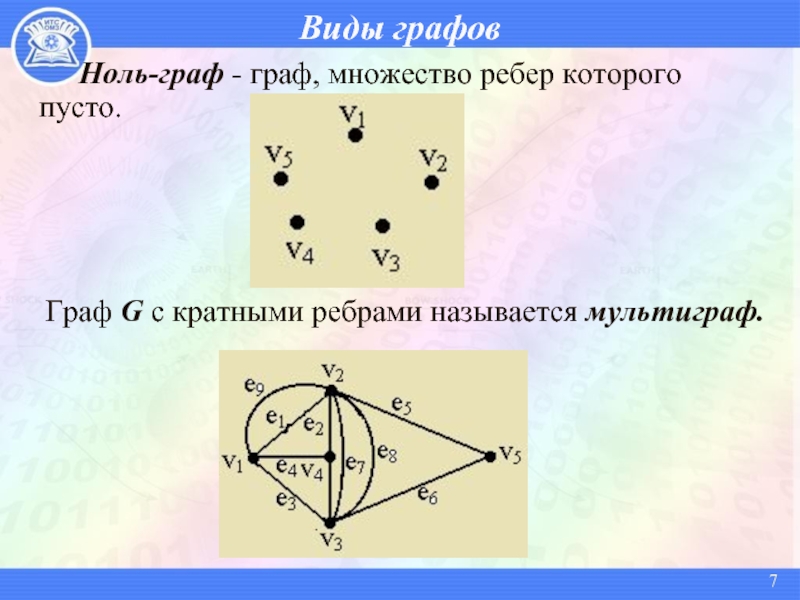
Проверяйте свой граф на циклы с кратными рёбрами, так как это может повлиять на точность алгоритмов поиска путей и других операций в графе.
Использование уникальных идентификаторов для рёбер может помочь избежать ошибок при добавлении новых связей и гарантировать отсутствие кратных рёбер.
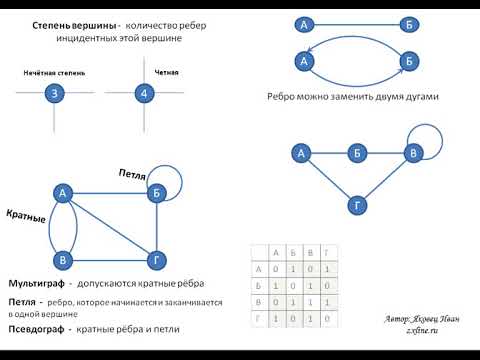
Графы, вершины, ребра, инцидентность, смежность

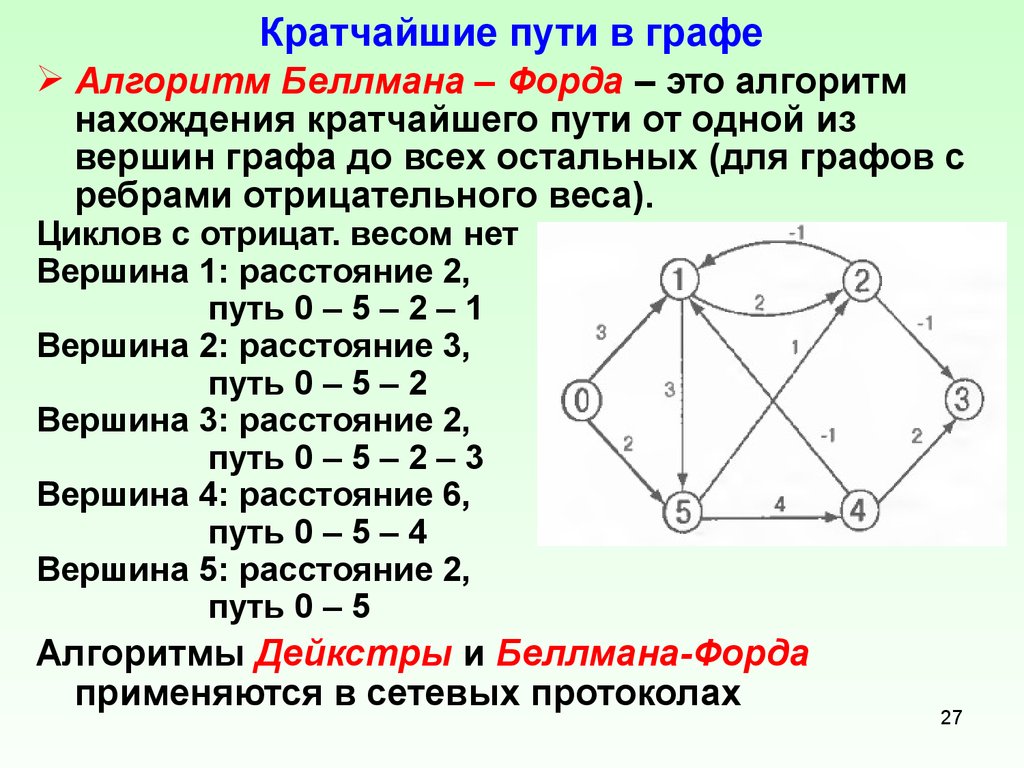
Не забывайте про возможное удаление лишних рёбер, если они образуют кратные связи, особенно в динамических графах, где структура может изменяться.
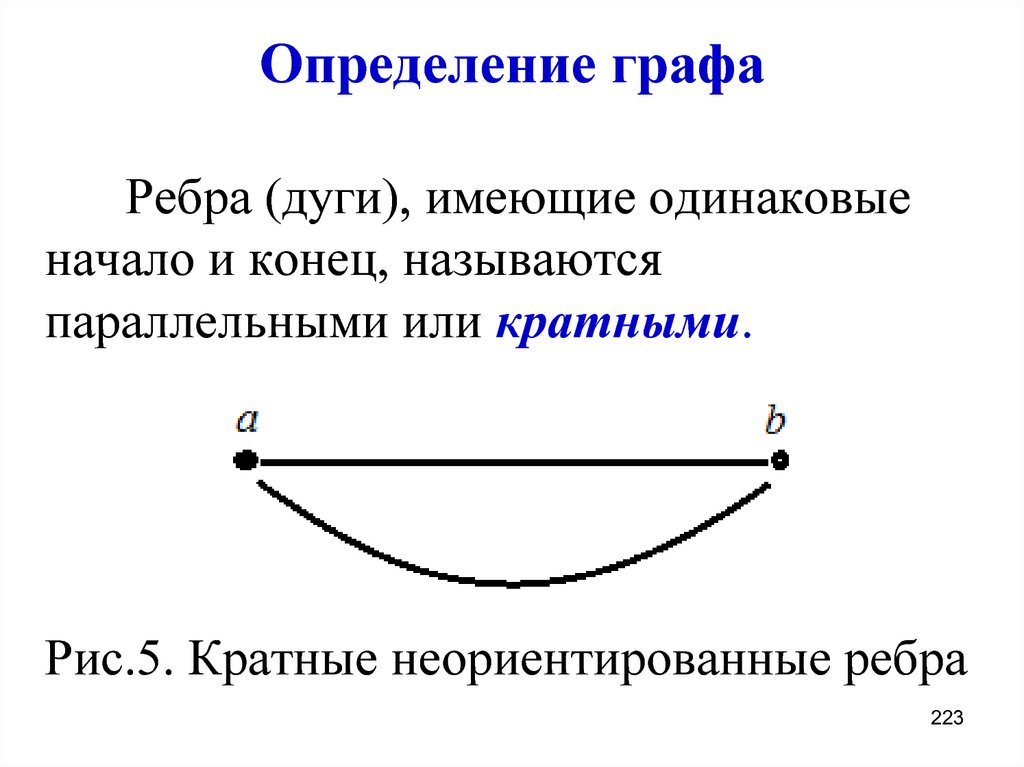
Используйте алгоритмы минимального остова, такие как алгоритм Прима или Краскала, чтобы исключить кратные рёбра при решении задач минимизации.
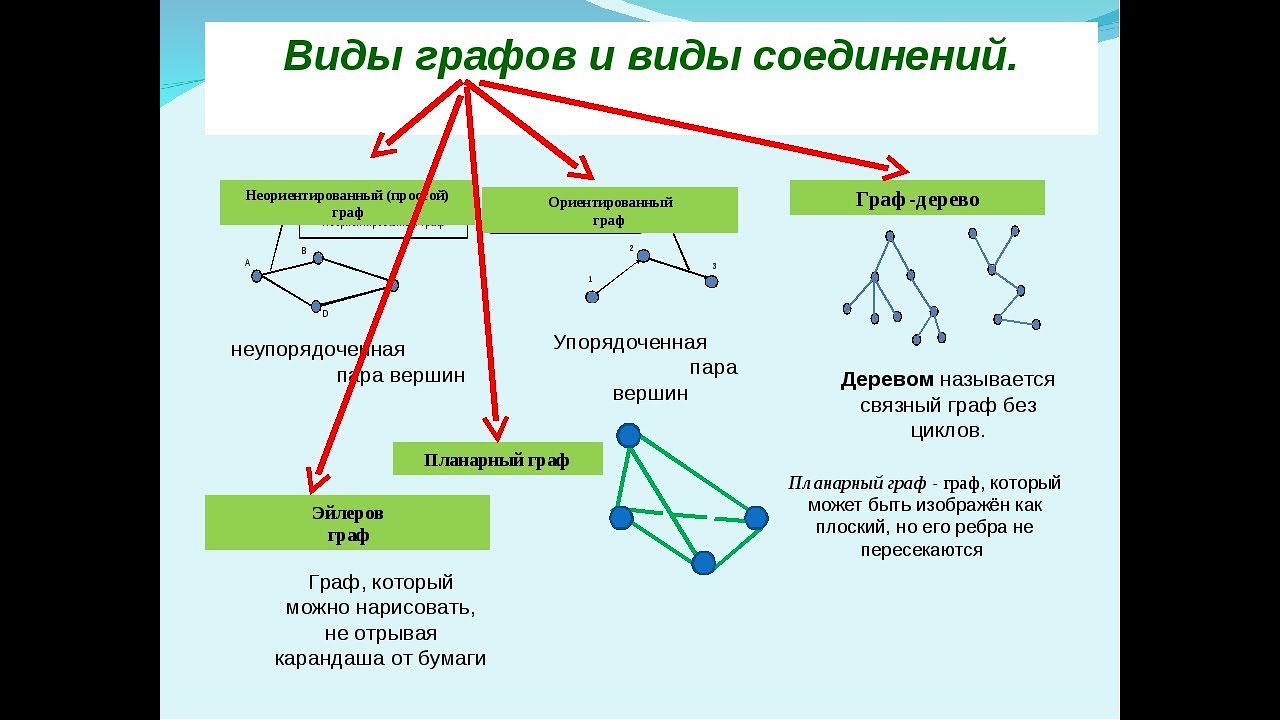
При работе с большими графами, следите за эффективностью ваших алгоритмов, так как проверка и удаление кратных рёбер могут существенно увеличивать время обработки данных.