Проверка дифференцируемости функции на интервале: что важно знать и как это делать
На этой странице мы расскажем, как правильно проверить, что функция дифференцируема на интервале. Здесь собраны полезные советы и рекомендации, которые помогут вам понять, как применяются теоремы и критерии дифференцируемости, а также как избежать распространенных ошибок при анализе функций.


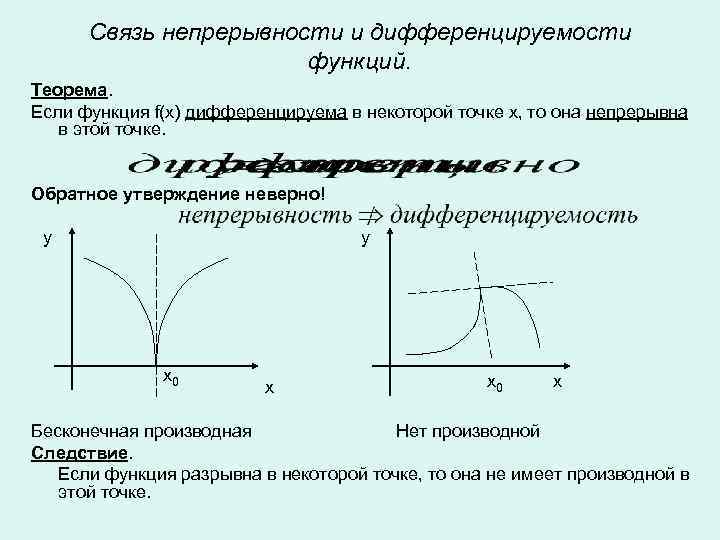
Для того чтобы функция была дифференцируема на интервале, она должна быть непрерывной на этом интервале.

Integrating ✏️✏️ a rate function gives 📶ACCUMULATION📶 #apcalculus #apcalc #unit8 #shorts

Дифференцируемость функции можно проверить с помощью определения производной через предел разности значений функции.

✓ Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин

Если функция представлена кусочно-заданной формой, необходимо проверять дифференцируемость в точках разрыва.
21. Дифференциал функции

Если функция имеет острые углы или вертикальные касательные, это может свидетельствовать о недифференцируемости в таких точках.
§ 4.10 Выпуклость функции и точки перегиба - Лекция 15 (2023) - Константин Правдин - НОЦМ ИТМО
Для проверки дифференцируемости на открытом интервале достаточно исследовать производную функции в каждой точке интервала.

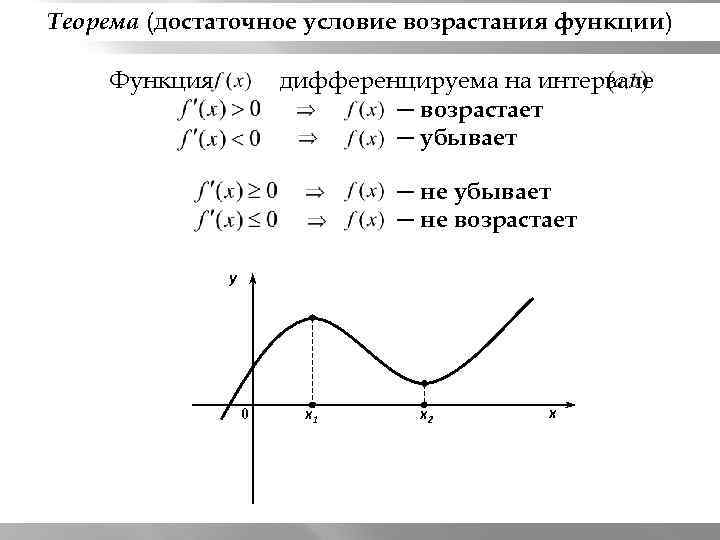
Возрастание и убывание функции на интервале, в точке. 2 семестр, 1 семинар


Использование критериев дифференцируемости, например, теоремы Ролля или Лагранжа, поможет упростить задачу.
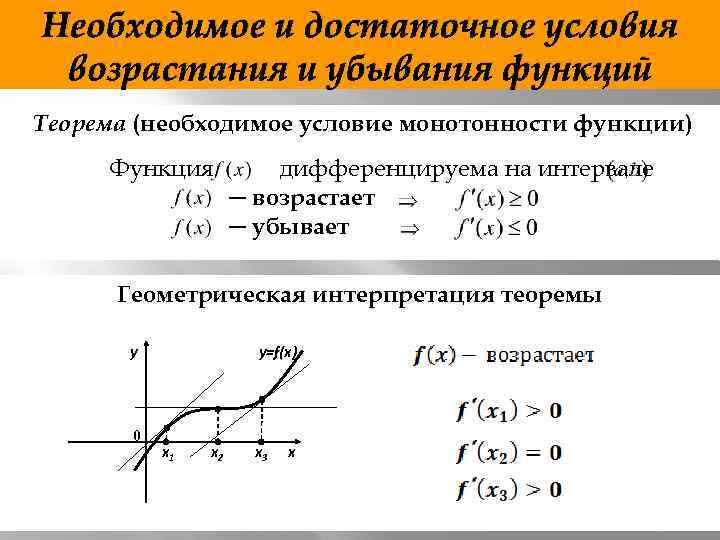
При исследовании дифференцируемости функций с параметрами важно учитывать, как параметры влияют на поведение функции на интервале.

Нули likerkacinema.ruщая функция на likerkacinema.ruление монотонности. Точка максимума/экстремума
Если функция содержит разрывы в интервале, то она не будет дифференцируема в точках разрыва.
Проверка существования производной в каждой точке интервала является важным этапом в определении дифференцируемости функции.

Continuous function- continuity in an interval

В случае функции нескольких переменных важно учитывать частные производные для каждой из переменных в каждой точке области определения.

Функция достигает наименьшего и наибольшего значения на интервале РЭШ


Дифференцирование комплексных функций (условия Коши-Римана и восстановление)