Шаг за шагом: как доказать свойство биссектрисы угла и его применения в геометрии
Доказательство свойства биссектрисы угла является важной задачей в геометрии, которая основывается на простых, но мощных теоремах. В этой статье мы расскажем о методах доказательства, которые помогут вам понять, как работает этот принцип и какие инструменты для этого можно использовать.
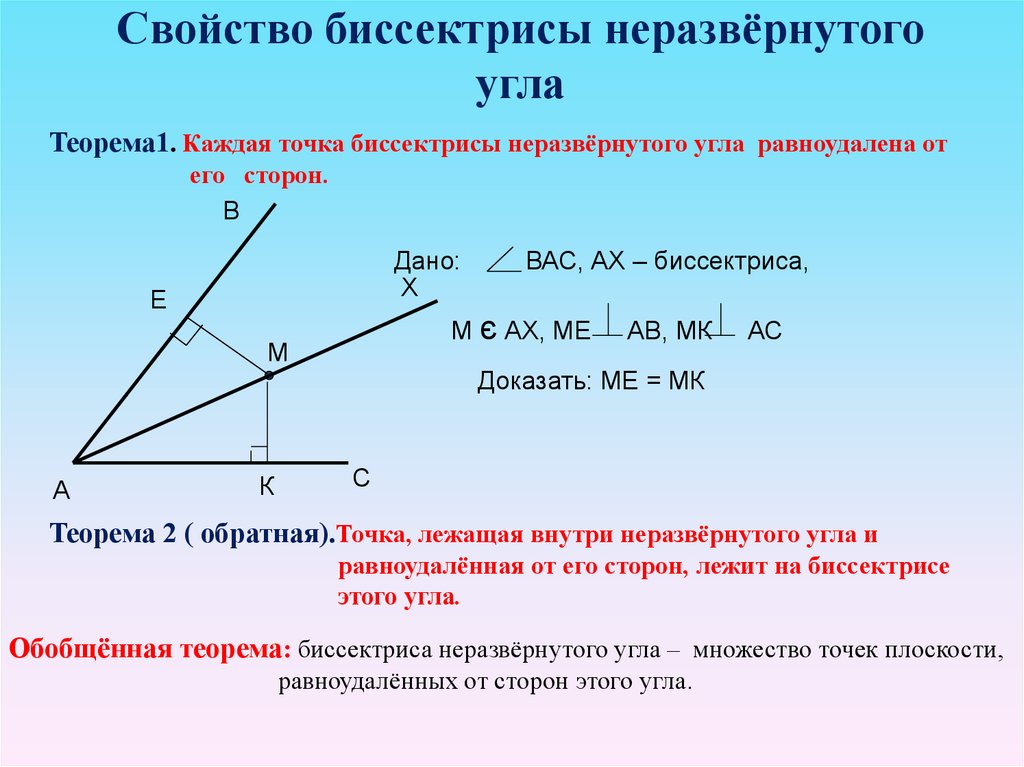
Начните с построения биссектрисы угла, чтобы наглядно понять, как она делит угол пополам.

74. Свойства биссектрисы угла
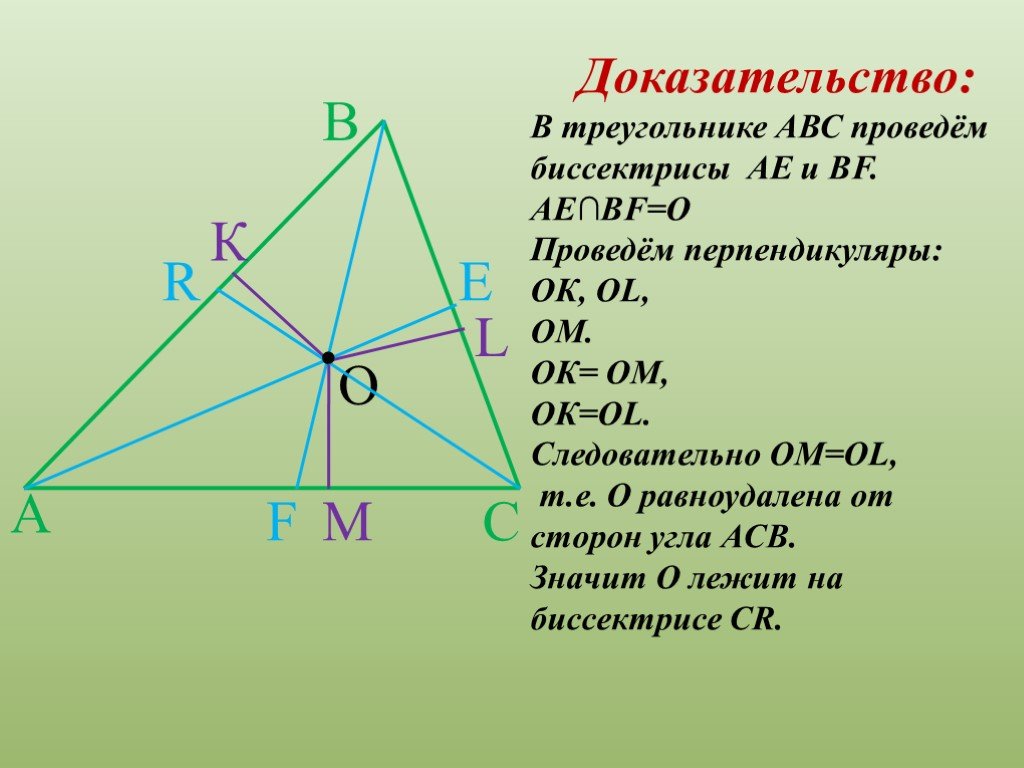
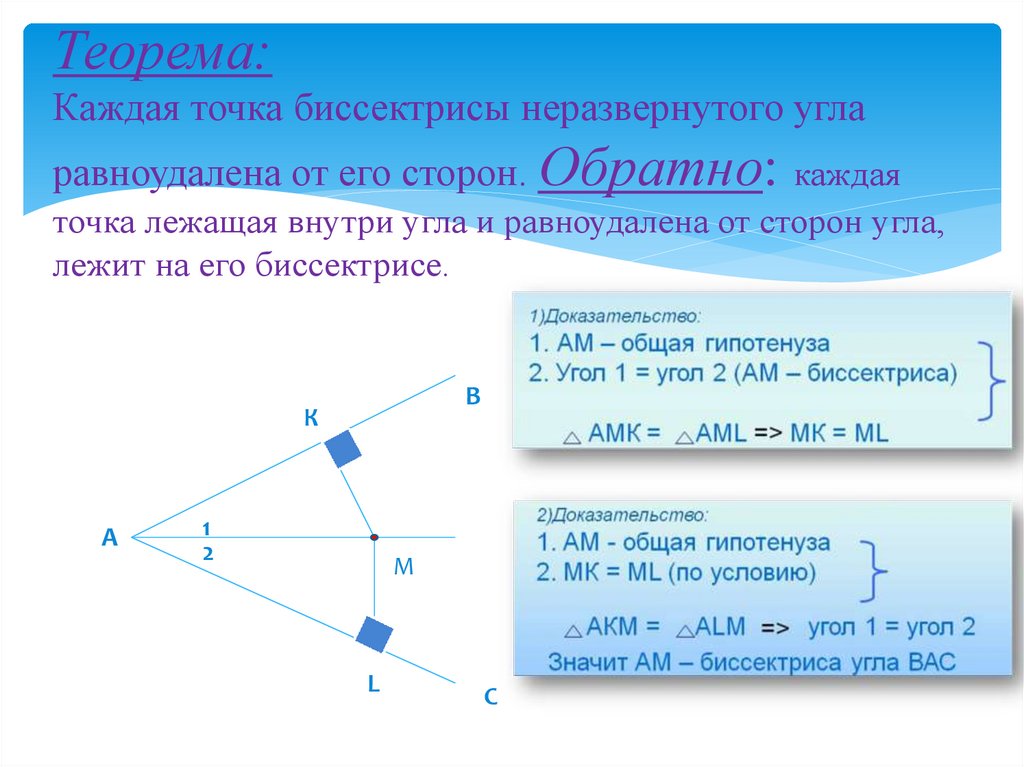
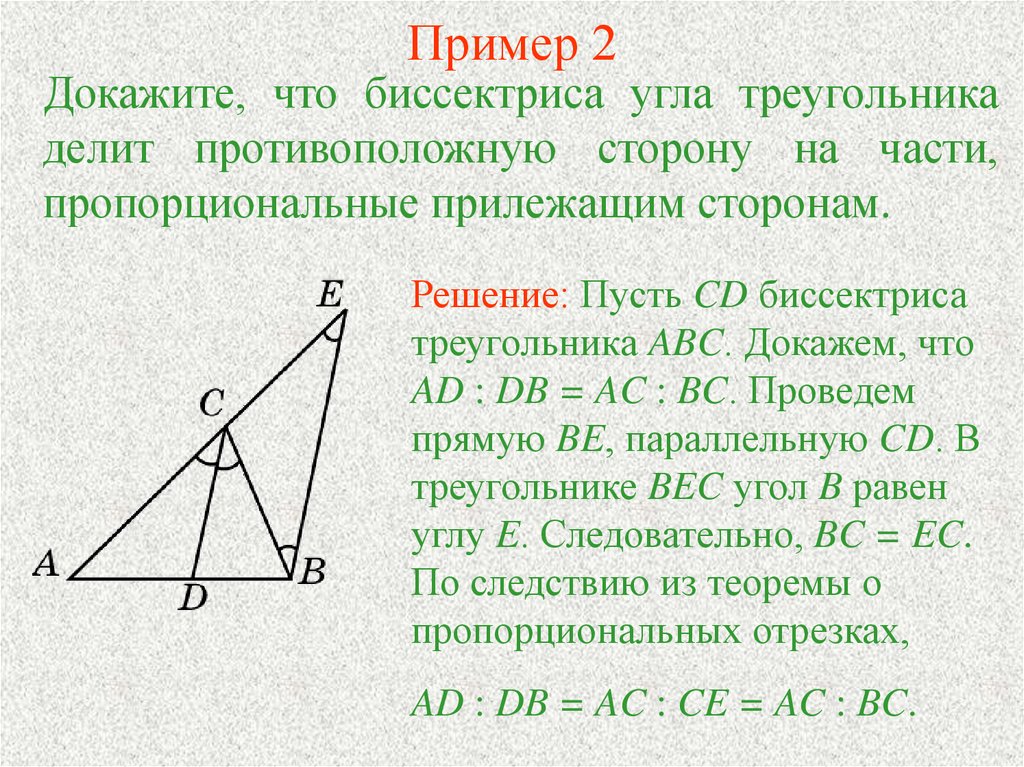
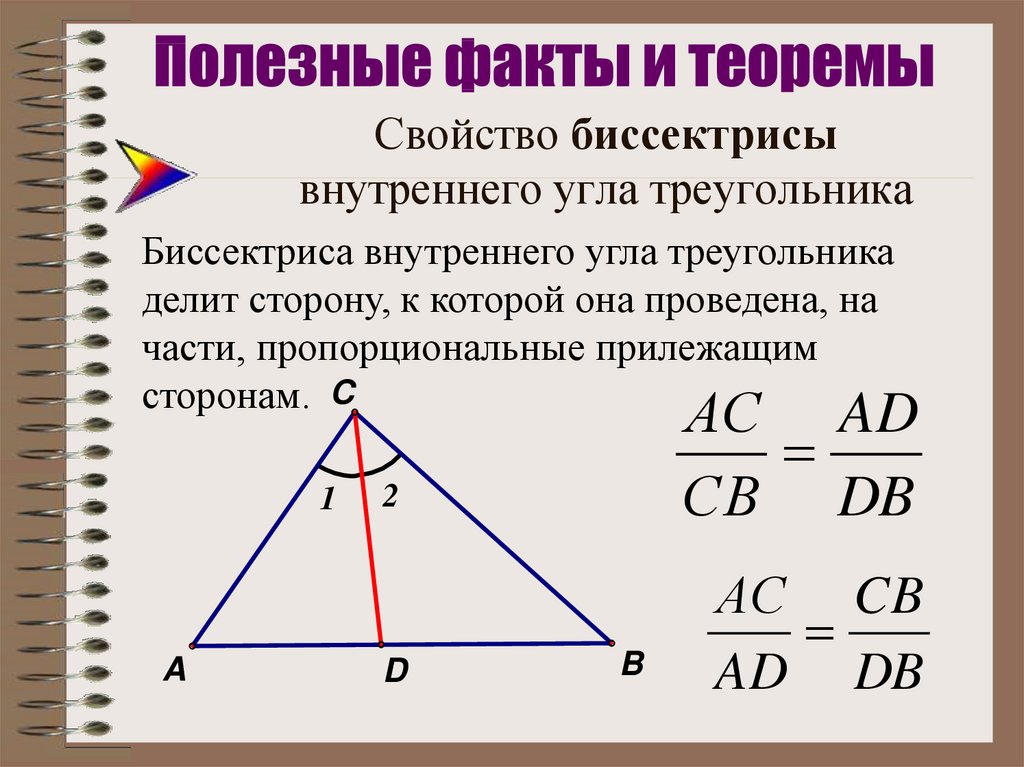
Используйте теорему о пропорциональности отрезков, чтобы подтвердить, что биссектрисы делят противоположные стороны угла в определенной пропорции.

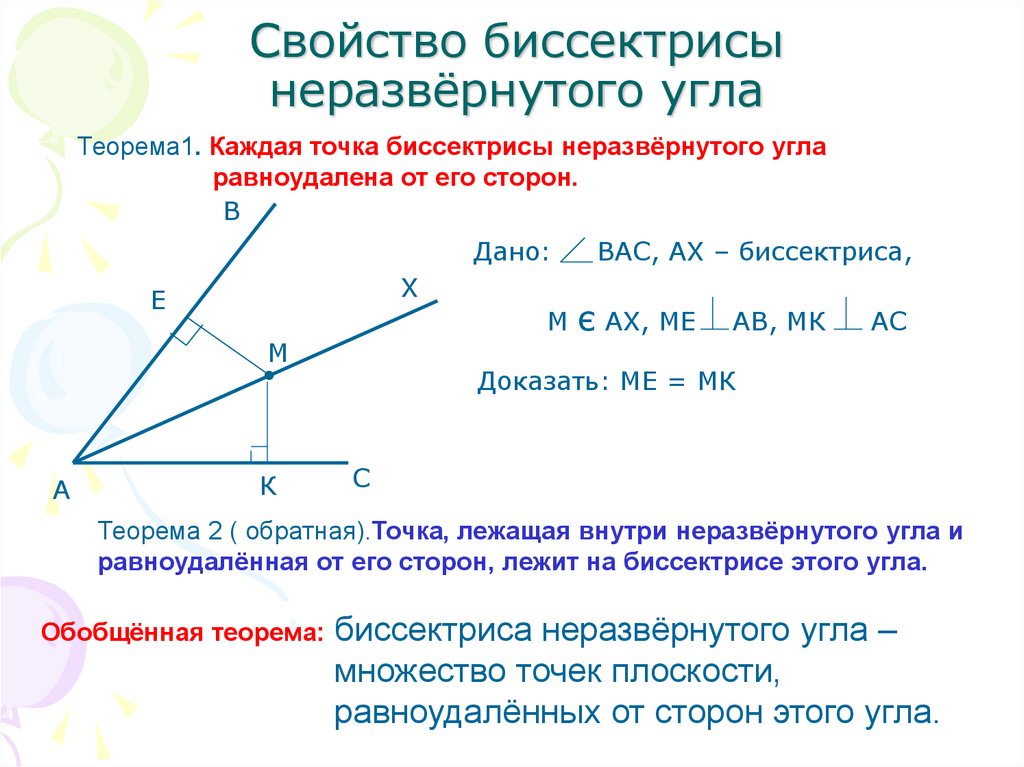
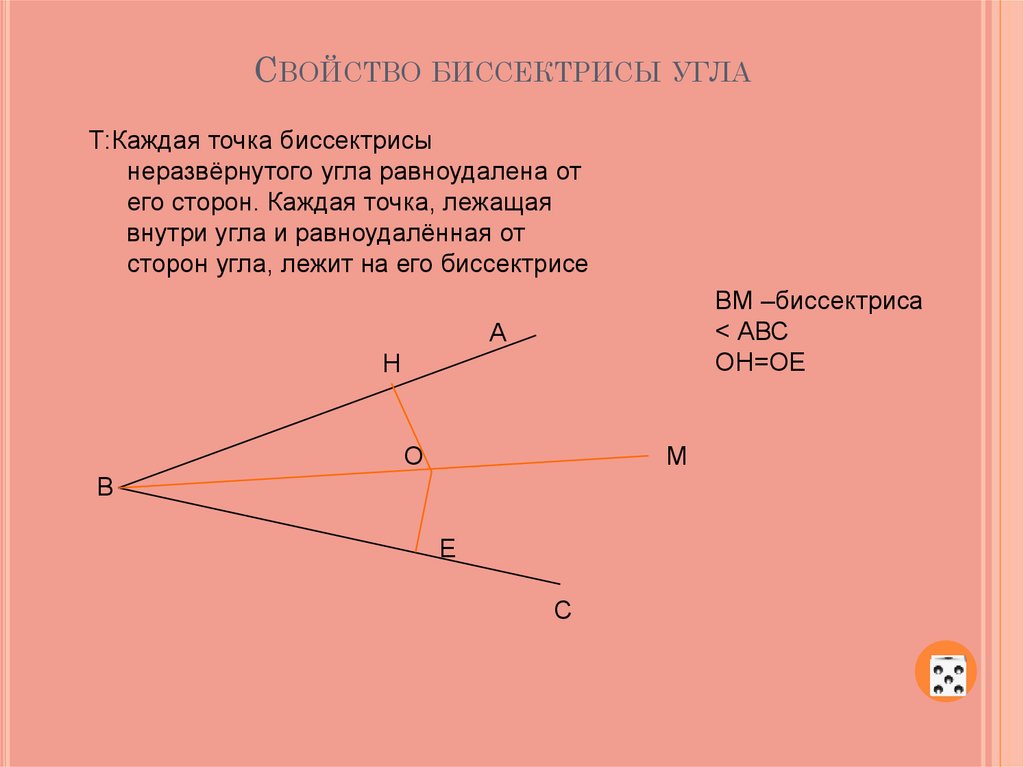
Построение биссектрисы угла
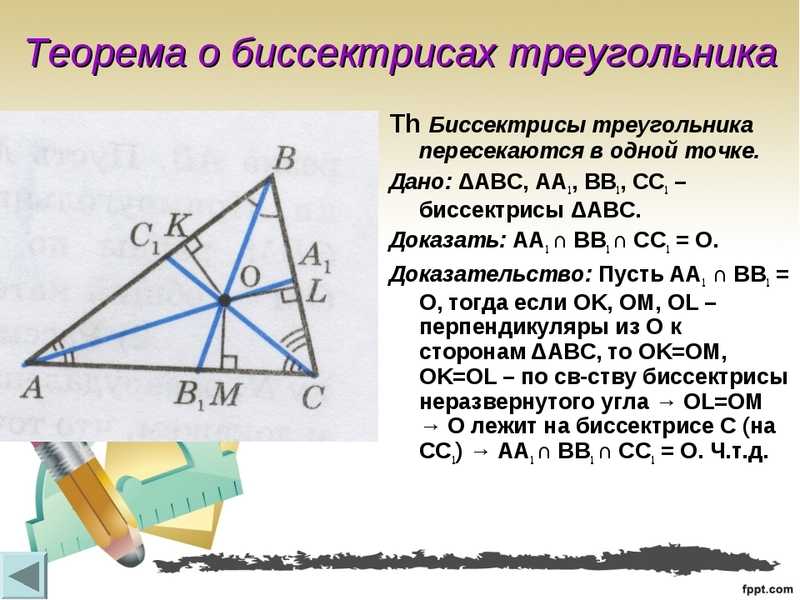

Не забывайте про свойство углов при пересечении двух прямых: они могут помочь в доказательстве равенства углов, образующихся при биссекции.
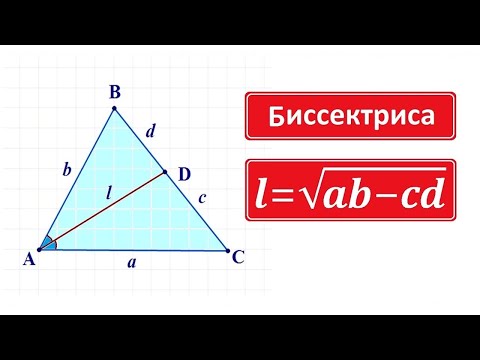
Формула для биссектрисы треугольника
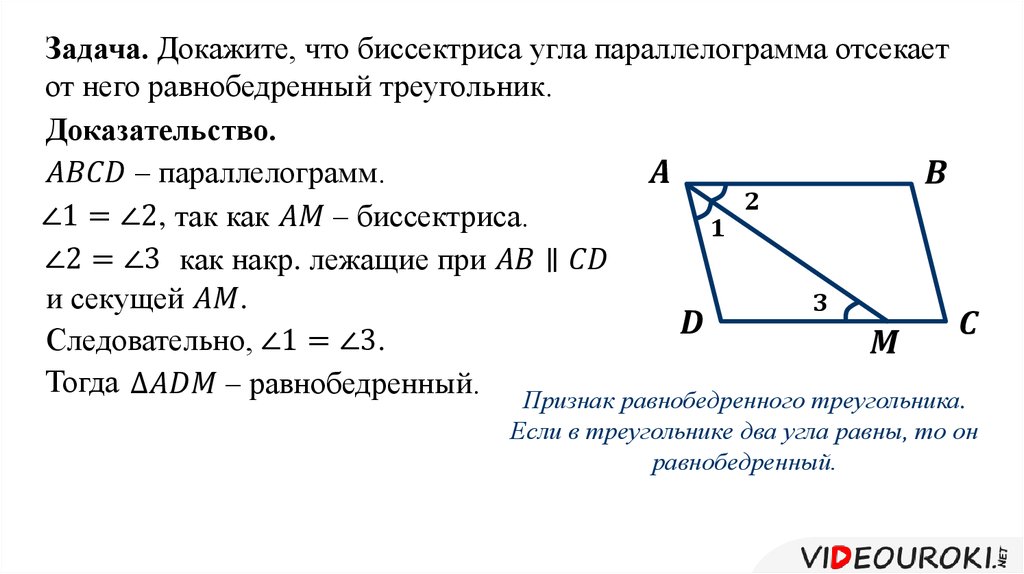
Для доказательства можно использовать метод контрпримера, если предполагаете, что свойство может не работать.

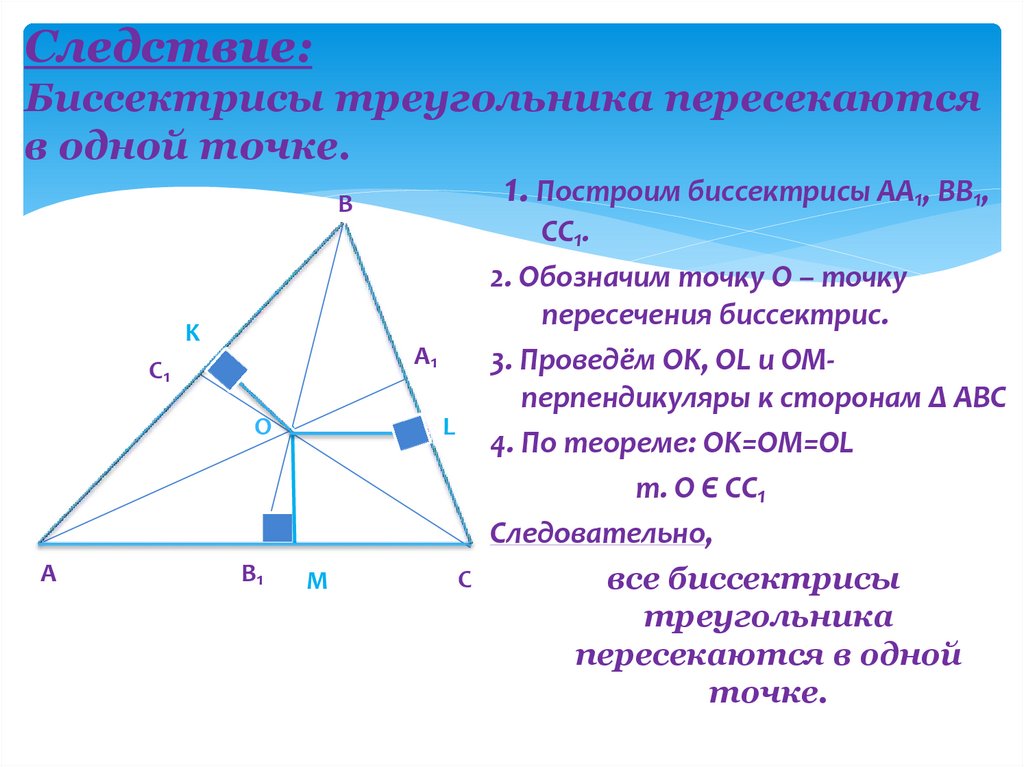
Свойство биссектрисы треугольника с доказательством
Применяйте теорему о равенстве углов, чтобы показать, что углы, образованные биссектрисой, равны.

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построение
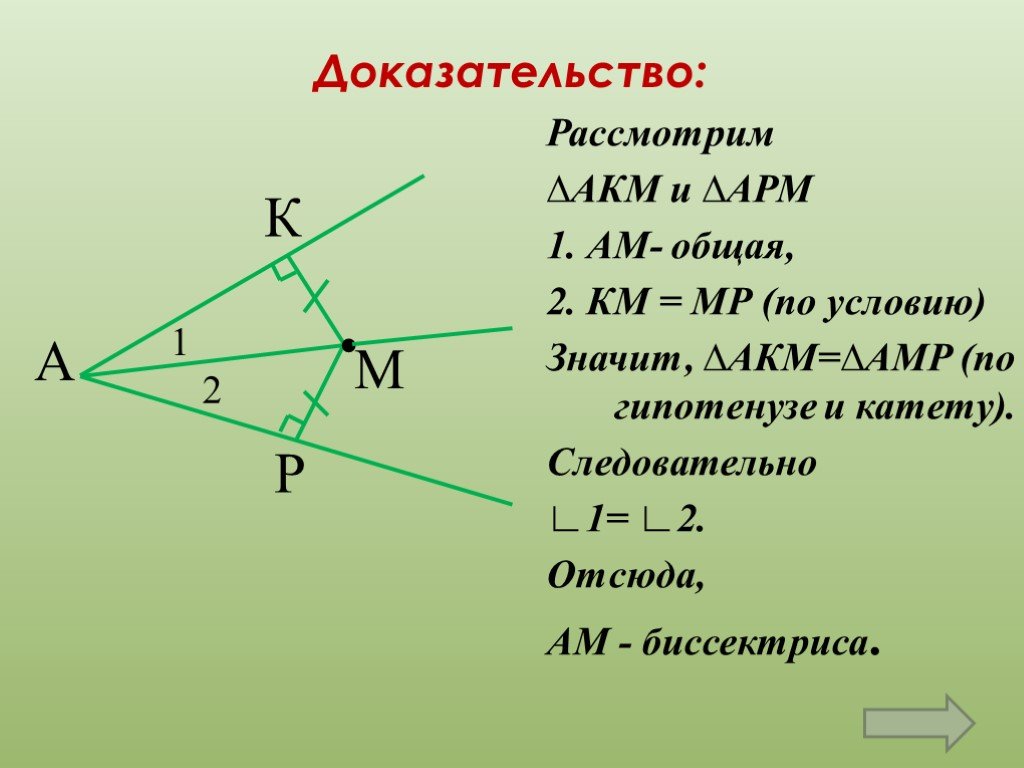

Важным моментом является использование вспомогательных построений, например, прямых, параллельных сторонам угла, чтобы упростить доказательства.

7 класс Задачи на построение Биссектриса угла
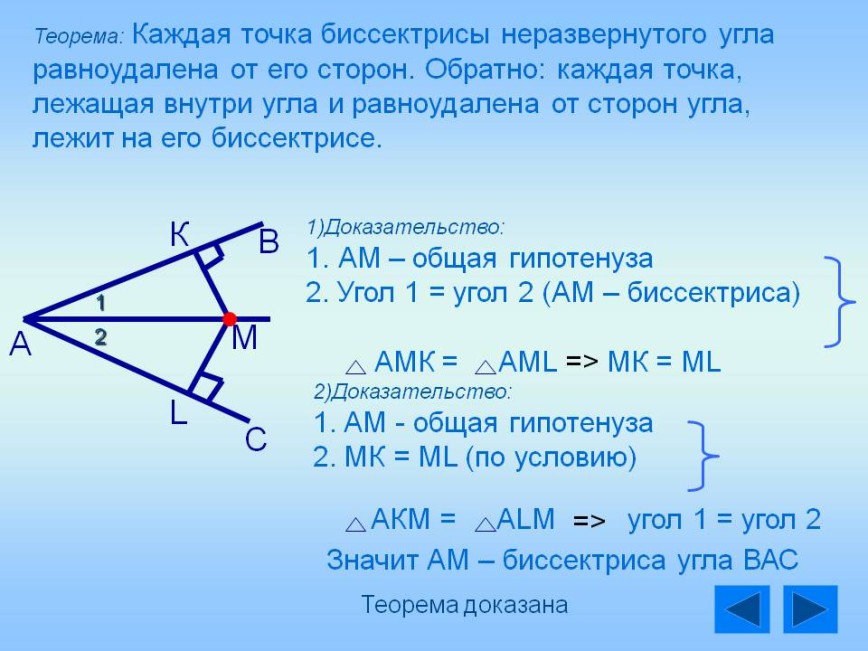
Проверяйте свои расчеты на симметрию: часто симметричные фигуры дают ключ к решению.
Определите, какие методы доказательства можно использовать в зависимости от исходных данных: через углы, стороны или пропорции отрезков.

Построение биссектрисы угла
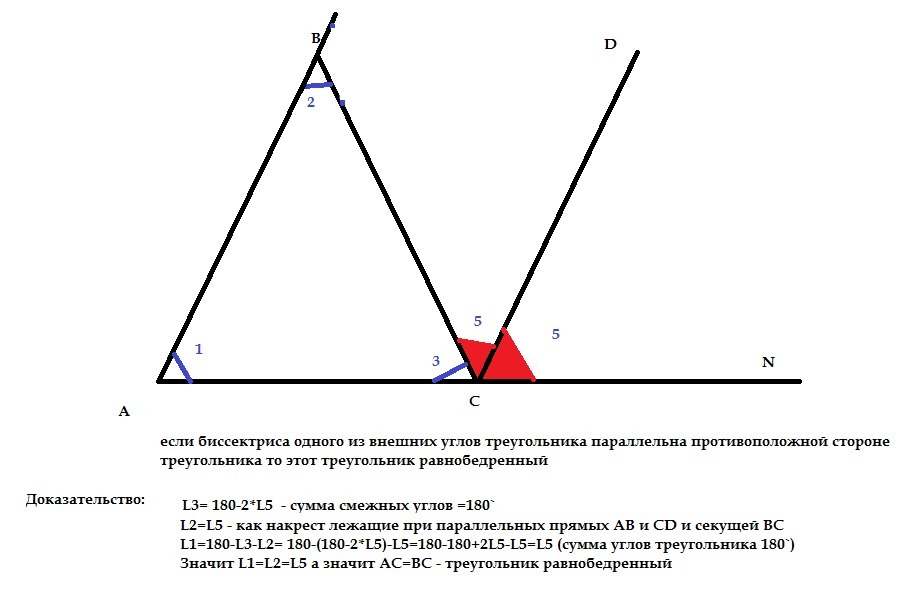

Обратите внимание на использование перпендикуляров и других вспомогательных линий для упрощения доказательства.

Урок по теме СВОЙСТВА БИССЕКТРИСЫ УГЛА 8 КЛАСС ГЕОМЕТРИЯ
Для более сложных доказательств рассмотрите использование координатной геометрии или аналитических методов, чтобы избежать трудных преобразований.

8 класс, 35 урок, Свойства биссектрисы угла


Построение биссектрисы угла. 7 класс.