Основные методы и полезные советы по нахождению диагональных сечений треугольных призм
Диагональное сечение треугольной призмы – это интересный и важный геометрический процесс, который позволяет понять структуру трехмерной фигуры через плоские сечения. В этой статье представлены полезные советы, которые помогут правильно ориентироваться в решении задач, связанных с этим сечением, а также визуализировать его на фотографиях и чертежах.
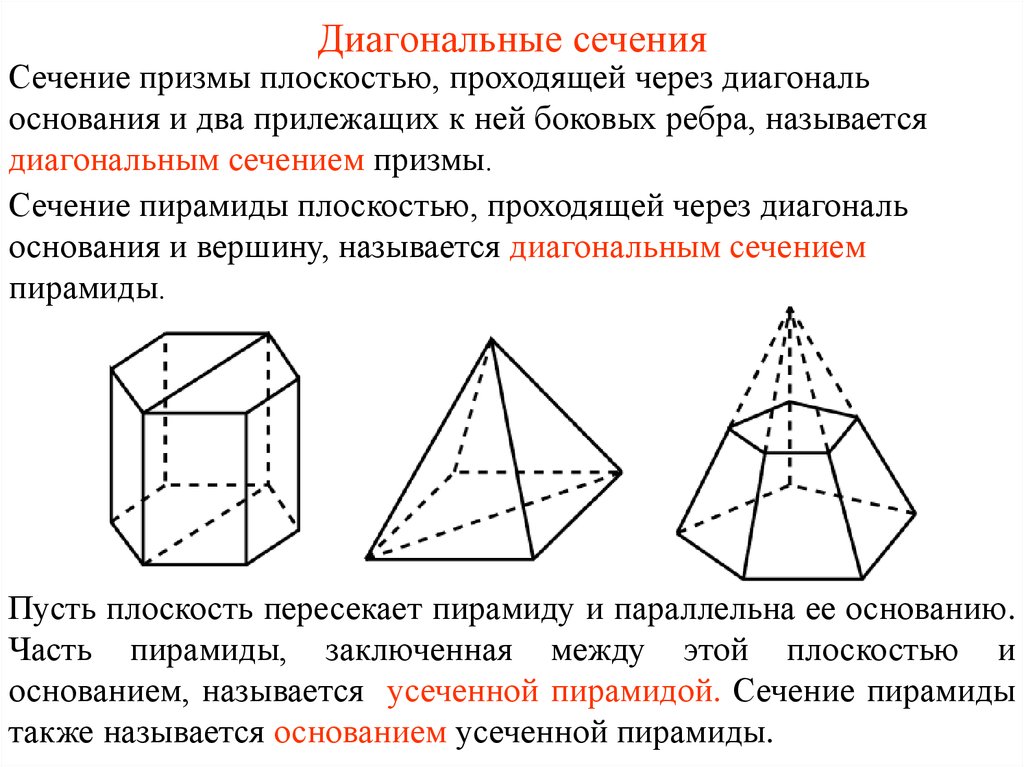
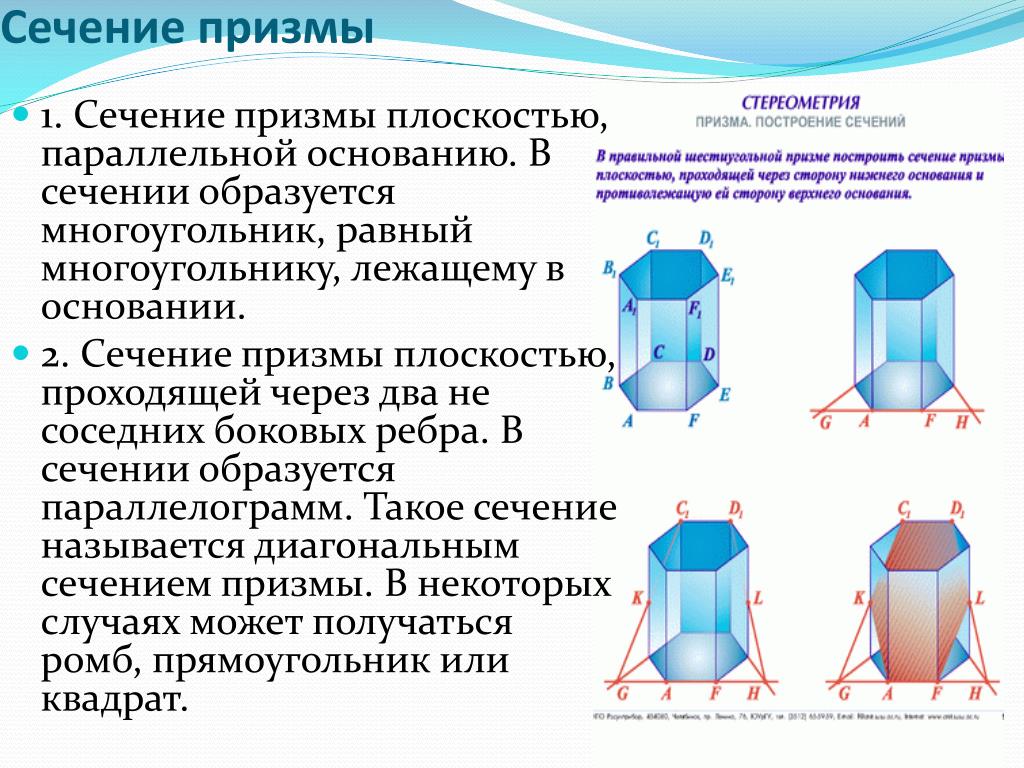
Для нахождения диагонального сечения важно правильно определить плоскость, в которой будет происходить сечение. Обычно такая плоскость пересекает несколько сторон призмы, создавая многогранник с особыми свойствами.

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИ
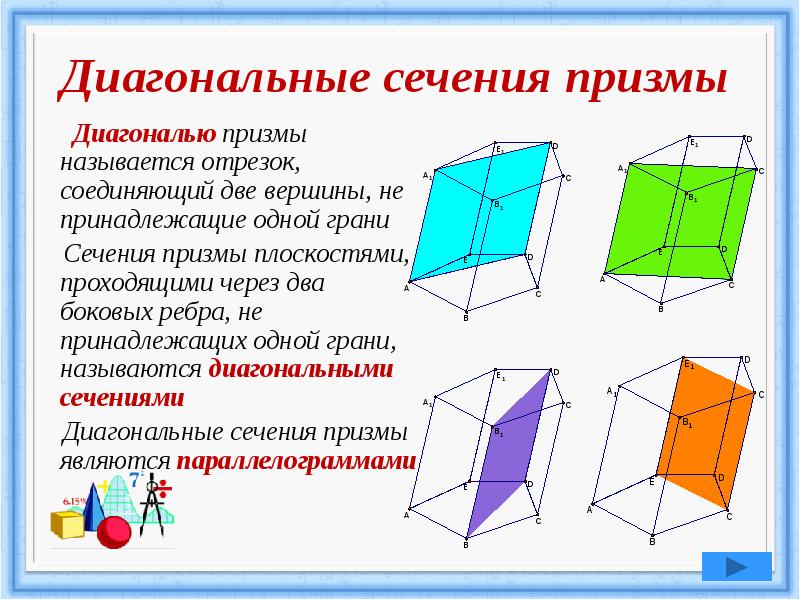
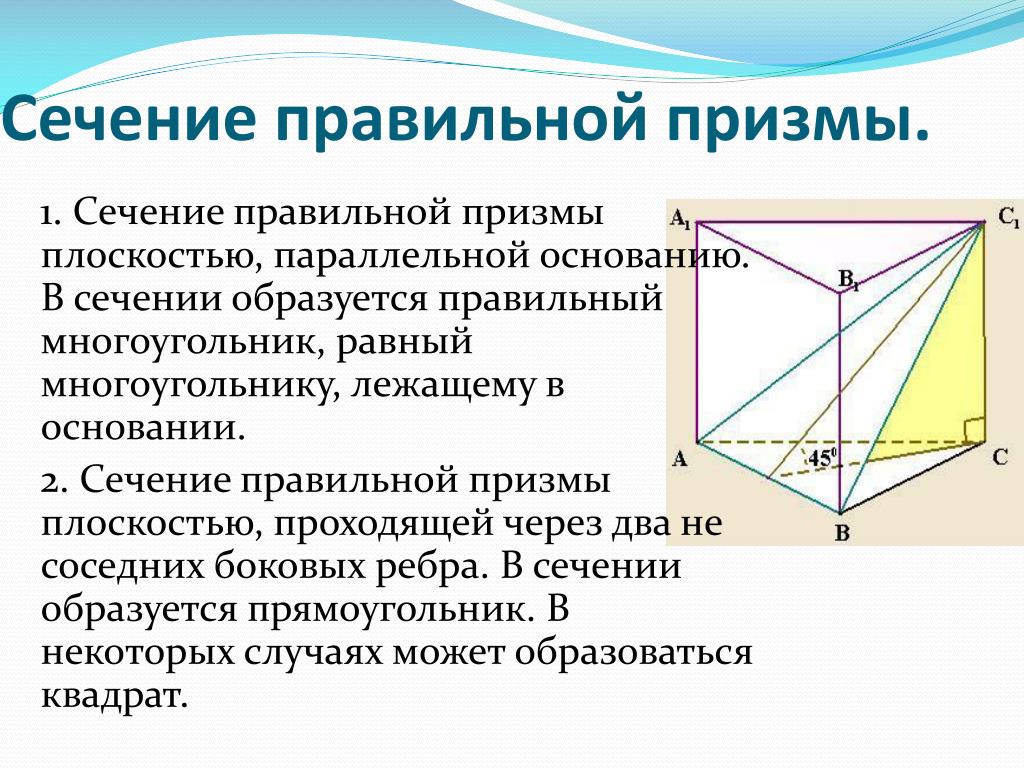
При выполнении диагонального сечения треугольной призмы, учтите, что сечение может быть не только треугольником, но и другим многоугольником, в зависимости от угла наклона плоскости.
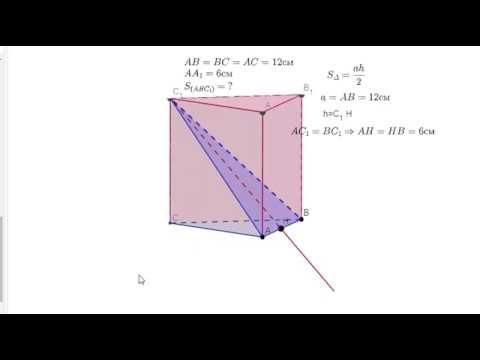
Призма. Площадь диагонального сечения. Теорема Пифагора в стереометрии.

Для визуализации диагонального сечения треугольной призмы лучше использовать графические программы или модели, которые позволяют динамично изменять угол сечения.

1 четверть, геометрия, 11 класс, ЕМН, 3 урок
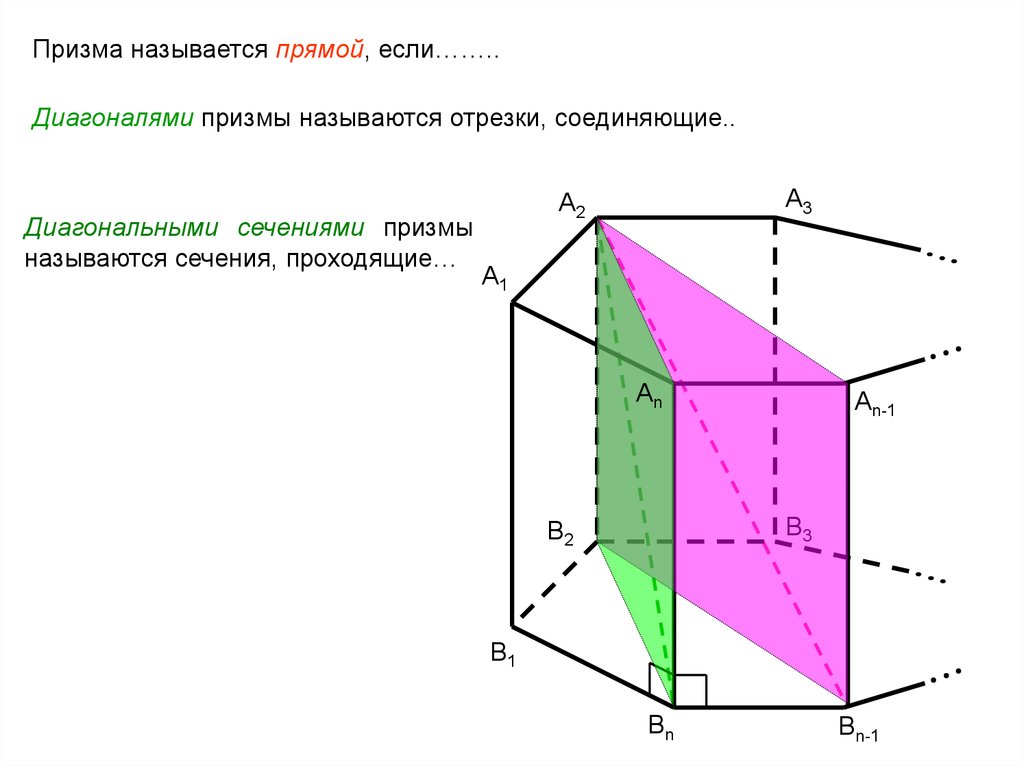
Обратите внимание на расположение точек пересечения сечения с гранями призмы. Это поможет вам точно определить форму сеченного многогранника.
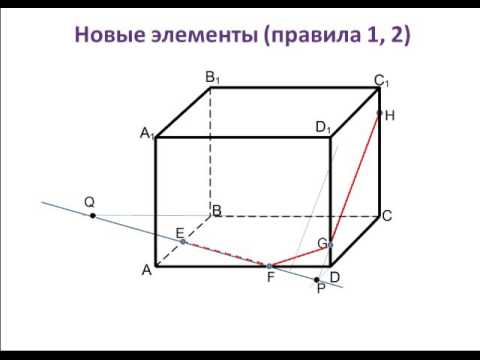
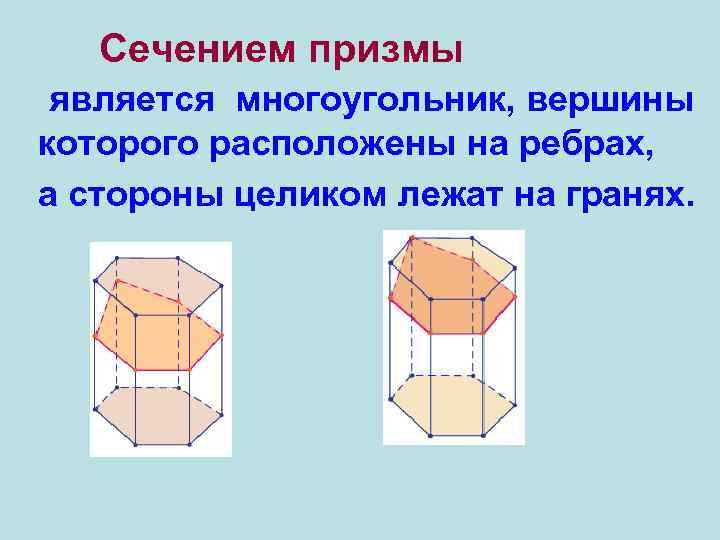
Сечение призмы плоскостью, заданной тремя точками
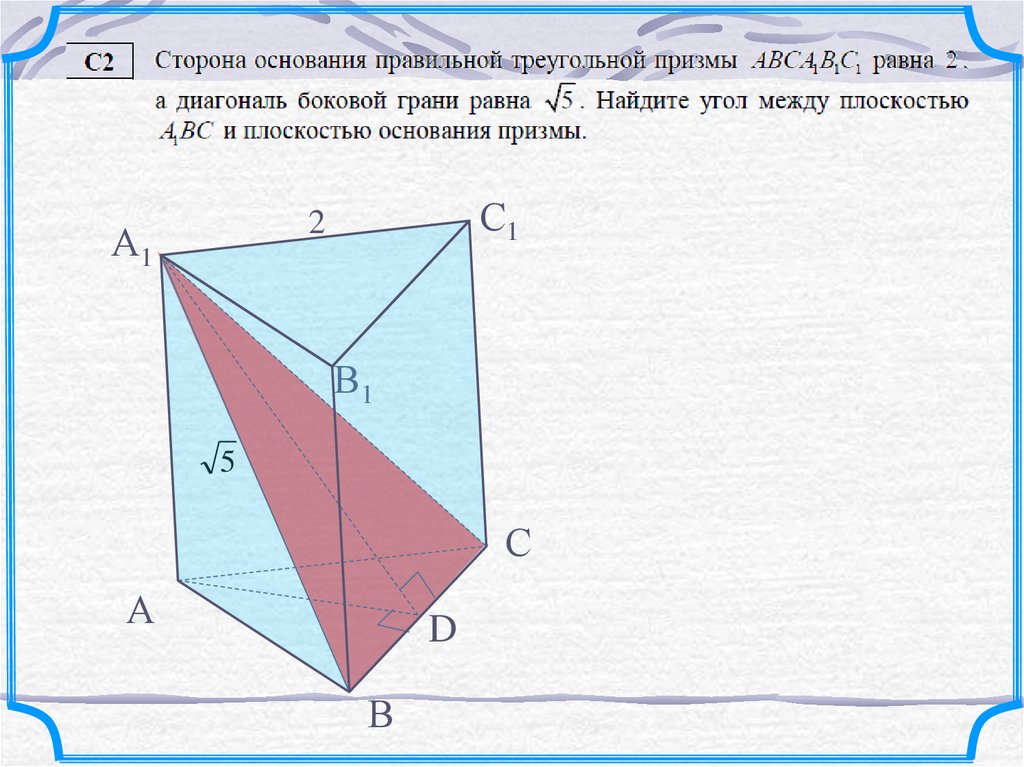
Для упрощения задачи нарисуйте проекцию треугольной призмы на плоскости, чтобы легче было понимать, как выглядит сечение на плоскости.
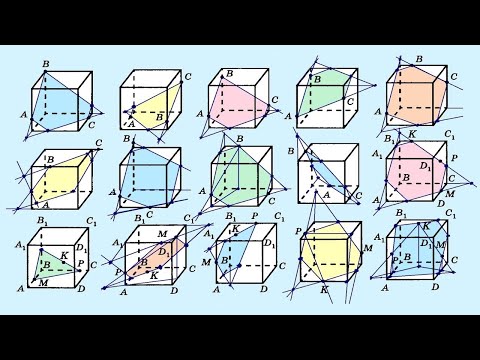
Как строить сечения
Секущая плоскость, пересекающая треугольную призму, может быть как параллельной одной из граней, так и наклонной. Важно правильно анализировать взаимное расположение этих элементов.
В задачах на диагональное сечение важно учитывать размер и форму самой призмы, а также её ориентацию относительно выбранной плоскости сечения.

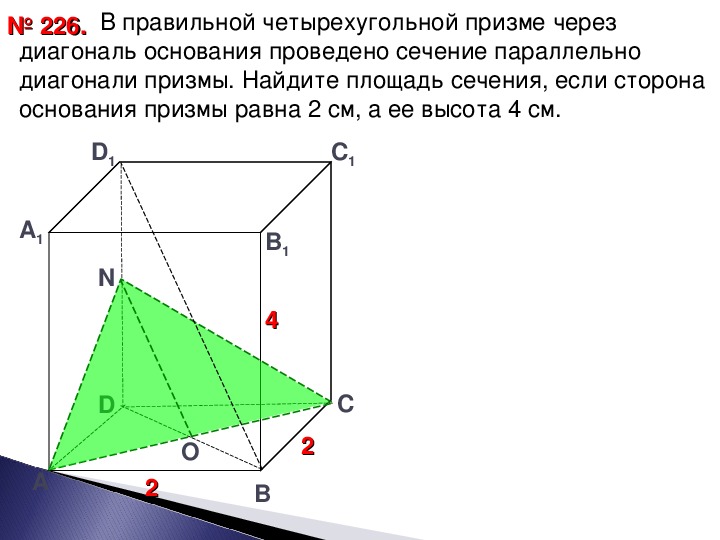
Не забывайте, что диагональное сечение может изменять видимость и форму граней, особенно если сечение проходит через вершины или ребра.

Все о призме .All about prism .
Если вам сложно представить сечение треугольной призмы, используйте модели в 3D, чтобы точнее понять, как работает сечение в реальном пространстве.

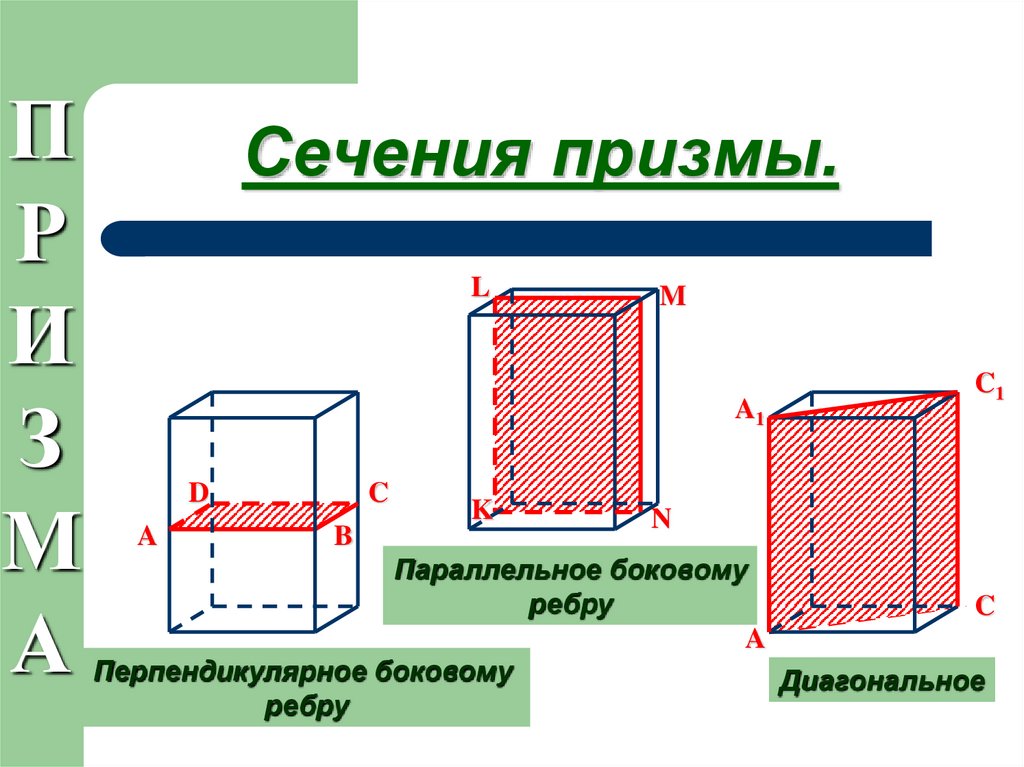
При решении задач на диагональное сечение треугольной призмы полезно начать с упрощенных примеров, чтобы затем переходить к более сложным случаям и моделям.
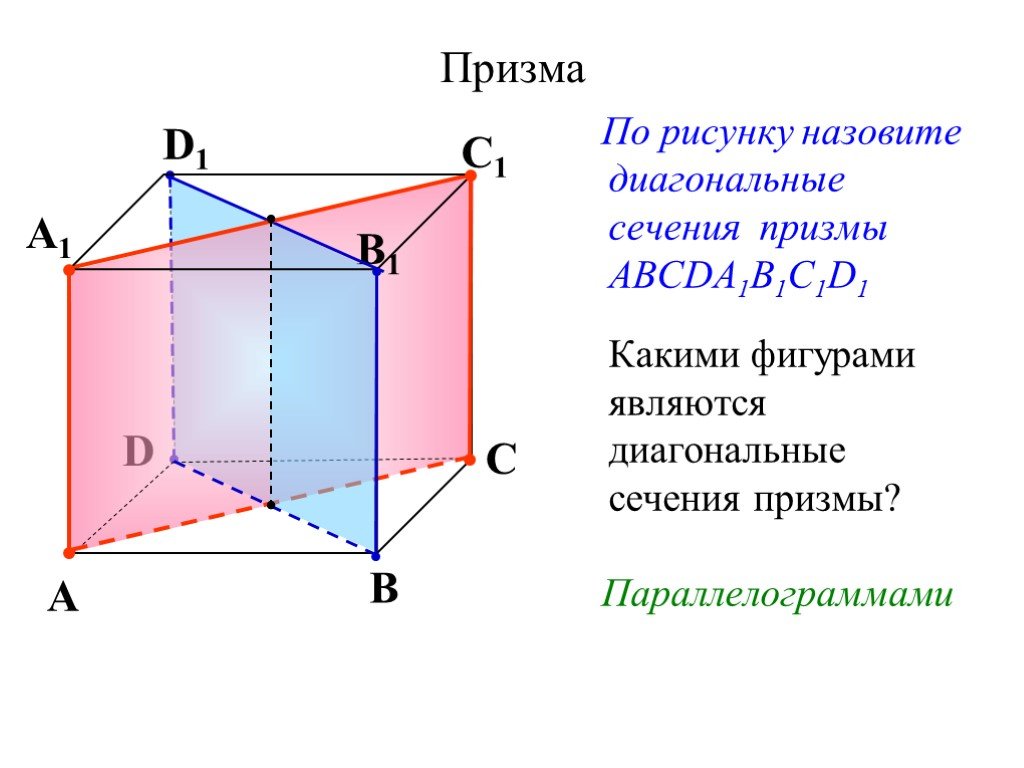
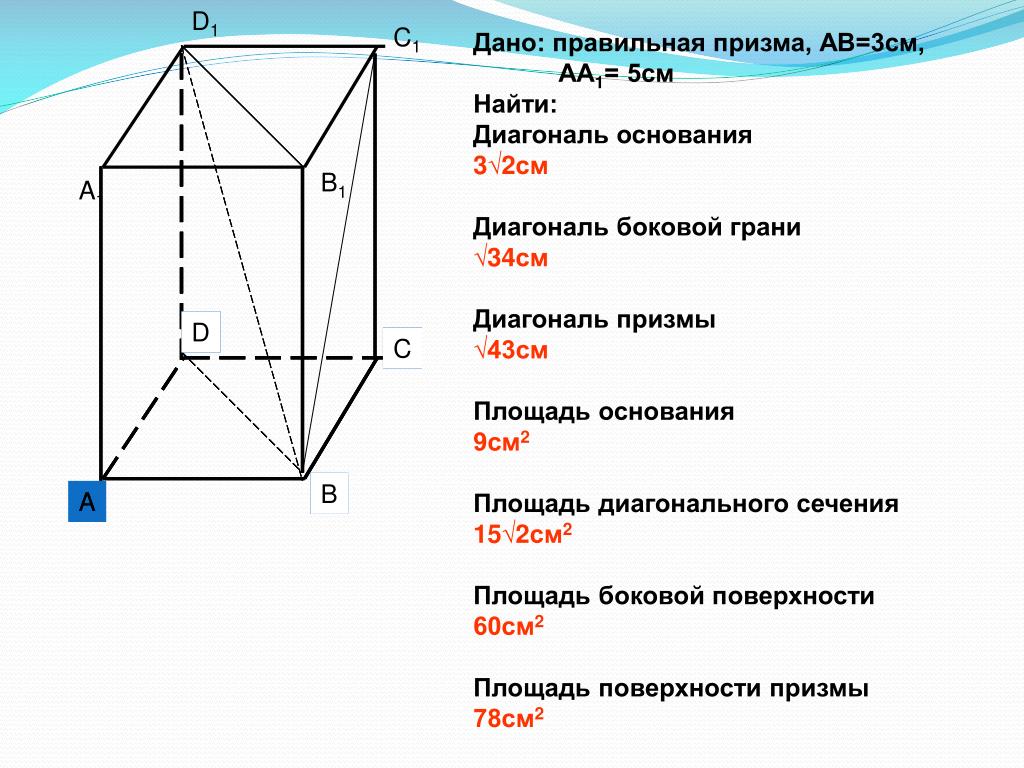
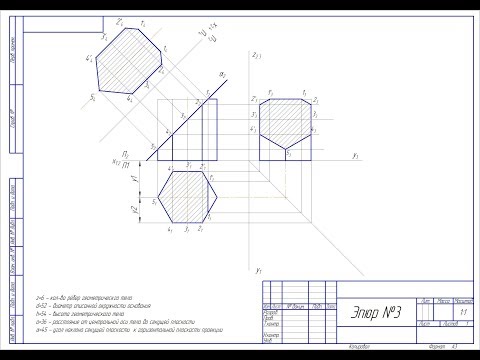
Урок #13│Сечение геометрического тела плоскостью│ Призма