Простое объяснение декартового базиса для практиков
Декартовый базис — это важный инструмент, используемый в математике и физике для описания пространства и анализа данных. На этой странице вы найдете красивые иллюстрации, понятные объяснения и полезные советы, которые помогут глубже разобраться в теме.


Начните изучение декартового базиса с основ: оси координат и их взаимное расположение.
алгебра 5-3 базис и действия над векторами в likerkacinema.ruнатах


Помните, что в декартовой системе оси перпендикулярны друг другу, образуя прямоугольный трёхмерный угол.

Выражение вектора через декартовый базис


Используйте наглядные модели или графические программы для лучшего понимания трёхмерных структур.

Алгебра и геометрия 4. Базисы и декартова система координат

При решении задач в декартовом базисе всегда отмечайте начало координат — точку (0,0,0).

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе
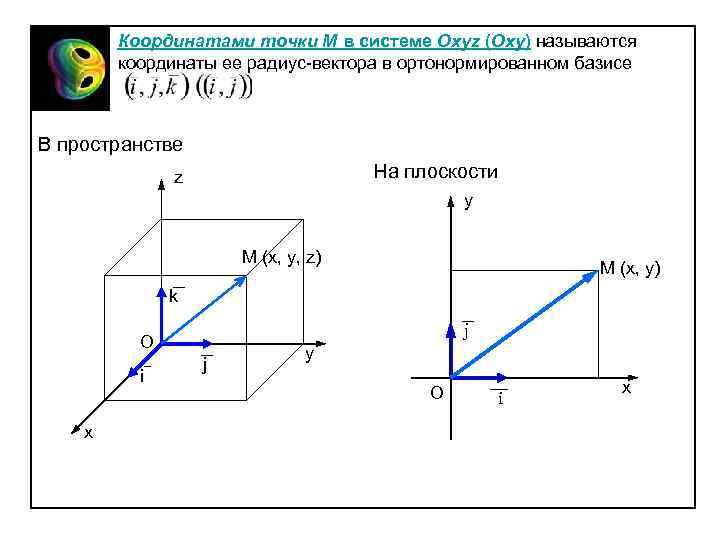
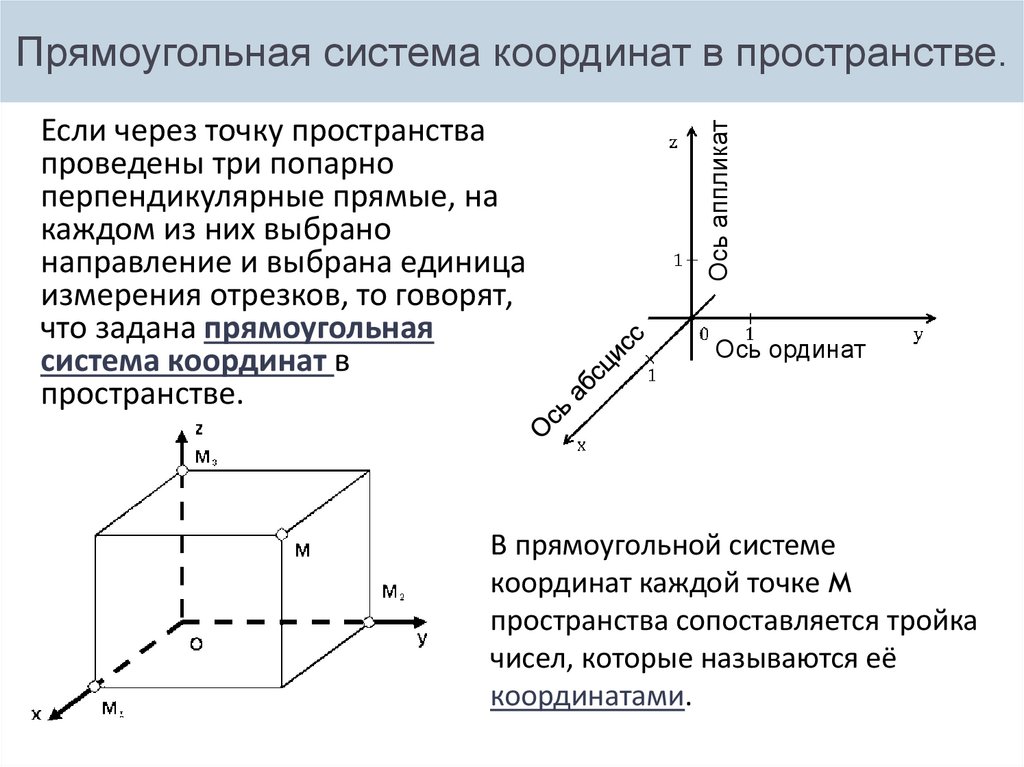
Если вы изучаете движение объектов, декартовый базис поможет точно описать их траекторию.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И АВТОМОБИЛИ. ВЕКТОР В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. УРОК 5


Практикуйте преобразование координат между разными системами, например, полярной и декартовой.

Базис векторов. (Векторная алгебра - урок 4)
Используйте цвета для выделения осей в графиках: это поможет избежать путаницы.

Разложение вектора в декартовой системе координат
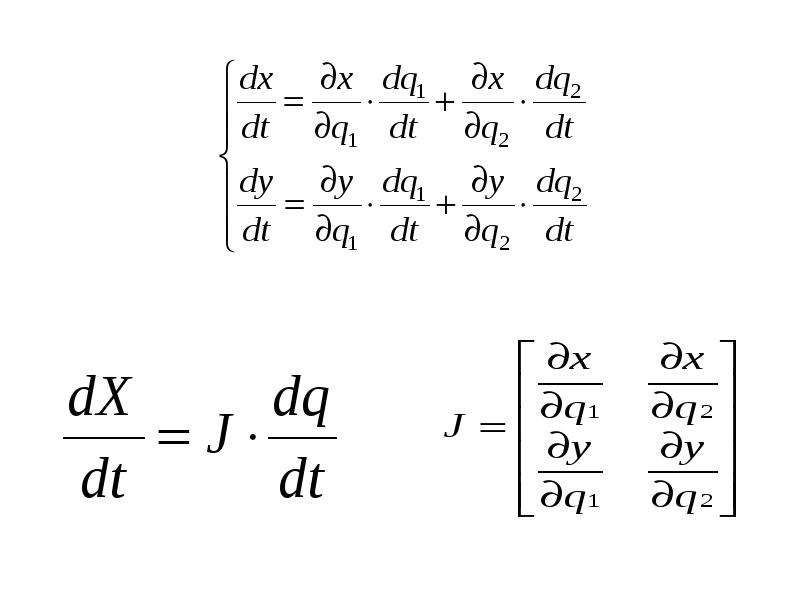

Решая задачи с векторами, помните, что их компоненты всегда записываются в виде чисел относительно осей базиса.
Изучите формулы длины, углов и расстояний в декартовой системе для практической работы с геометрией.

Применяйте знания о декартовом базисе для анализа реальных данных, например, в инженерии или программировании.

Базис. Разложение вектора по базису.



4.2. Вектор. Базис