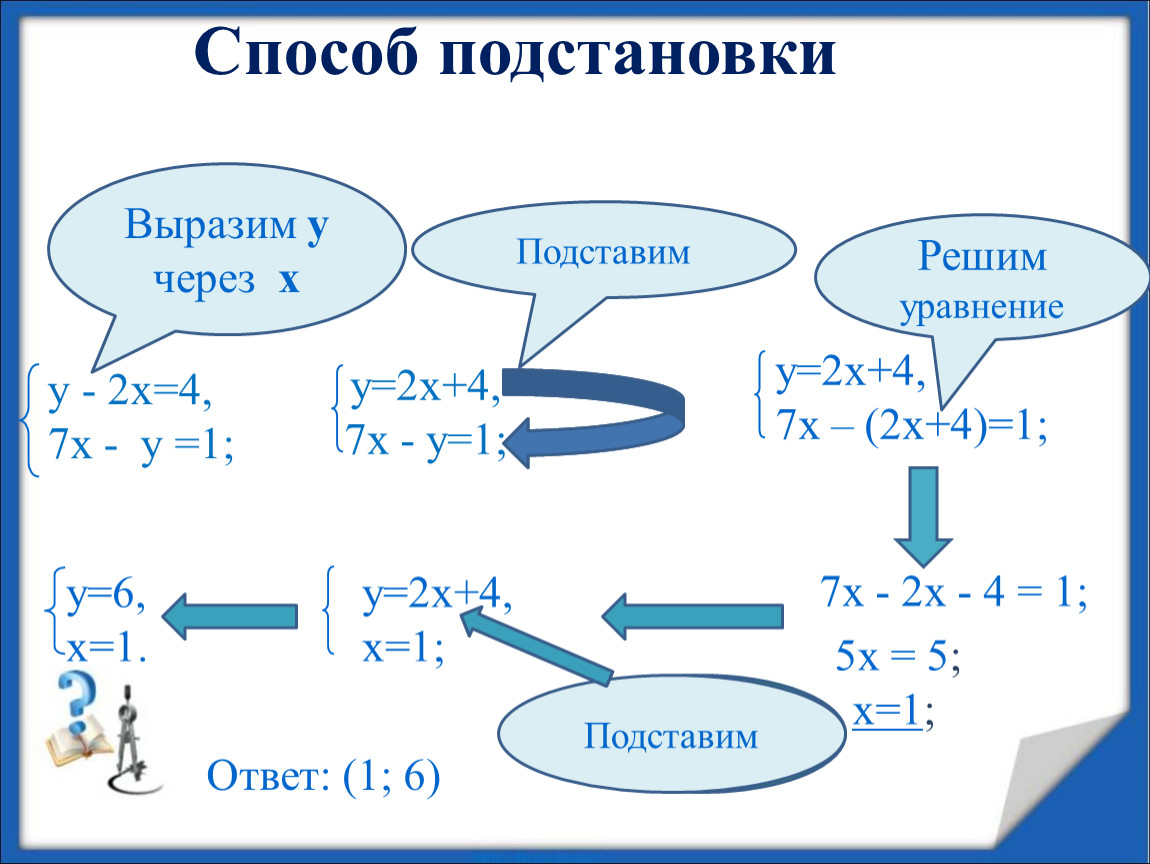
Пошаговое объяснение метода подстановки для решения уравнений

Метод подстановки — это популярный способ решения системы линейных уравнений, при котором одно из уравнений преобразуется так, чтобы одна из переменных была выражена через другие. После этого это выражение подставляется в другое уравнение, что позволяет найти все переменные системы. Метод подстановки особенно удобен, когда одно из уравнений легко преобразуется для подстановки. Важно учитывать последовательность шагов, чтобы избежать ошибок в расчетах и получить правильный результат.

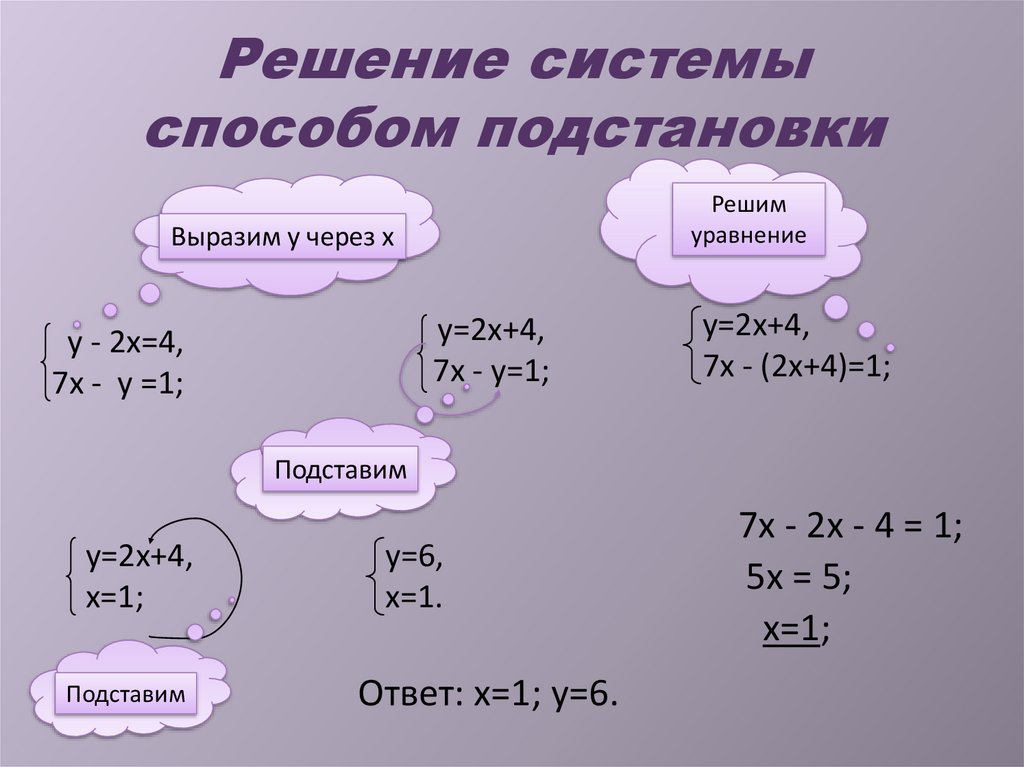
Начинайте решение с выбора уравнения, в котором проще выразить одну переменную через другую.

Подставляйте найденное выражение аккуратно, следя за порядком действий и правильностью знаков.

Не забывайте, что при подстановке дробей лучше избавиться от знаменателей, умножив обе части уравнения на общий знаменатель.

Проверяйте результат после подстановки в исходные уравнения, чтобы убедиться в его корректности.

Если результат не совпадает, проверьте, не ошиблись ли вы в математических операциях на этапе подстановки.

Для более сложных систем попробуйте решить уравнение поочередно для каждой переменной, если это возможно.

Если система уравнений имеет бесконечное множество решений, убедитесь, что это отражается в математическом выводе.

При решении системы методом подстановки старайтесь использовать как можно более простые уравнения для выражения переменных.

Записывайте каждый шаг, чтобы в случае ошибки можно было быстро найти её причину.

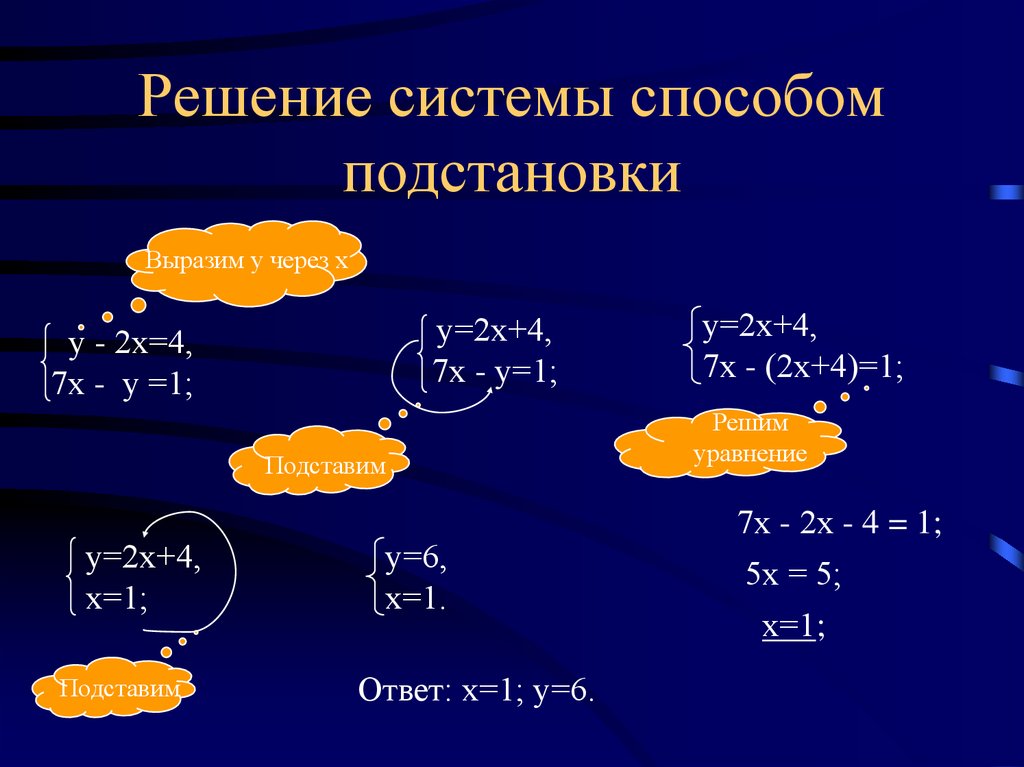
Метод подстановки можно применять не только для линейных уравнений, но и для систем, содержащих квадратные или другие выражения, если это удобно.