Что важно знать о высоте треугольника в геометрии 7 класса
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или её продолжение. Важно понимать, что высота может быть внутри треугольника, если он остроугольный, и снаружи, если он тупоугольный. В 7 классе учащиеся знакомятся с этим понятием в рамках изучения свойств различных типов треугольников и их вычислений.
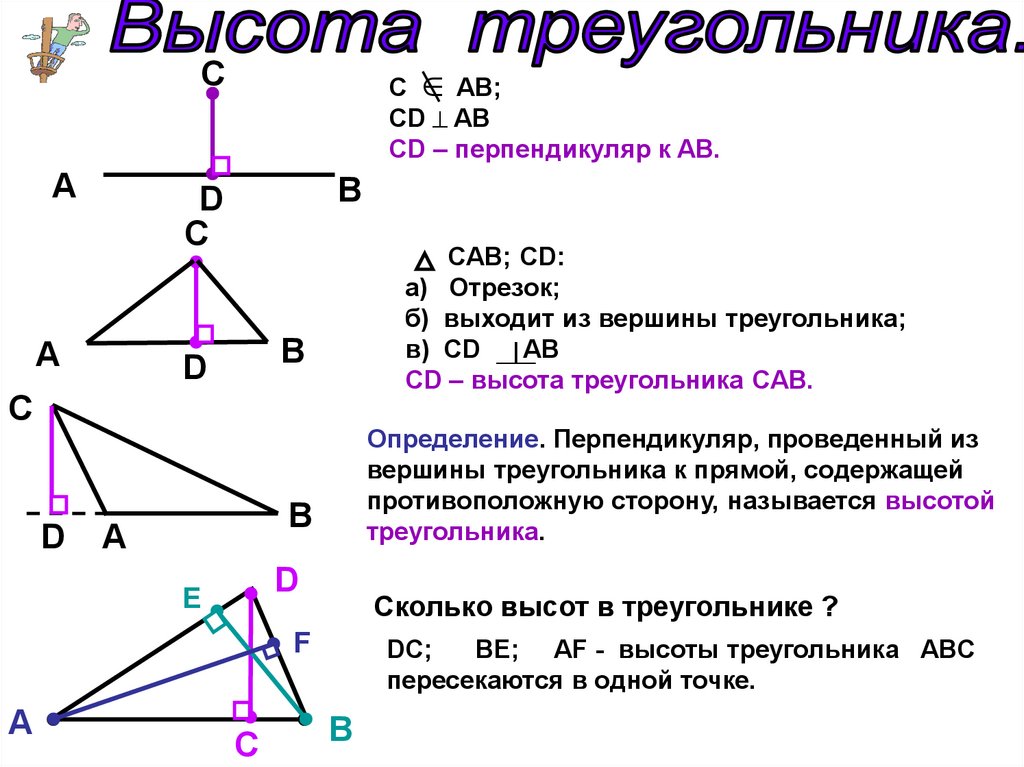
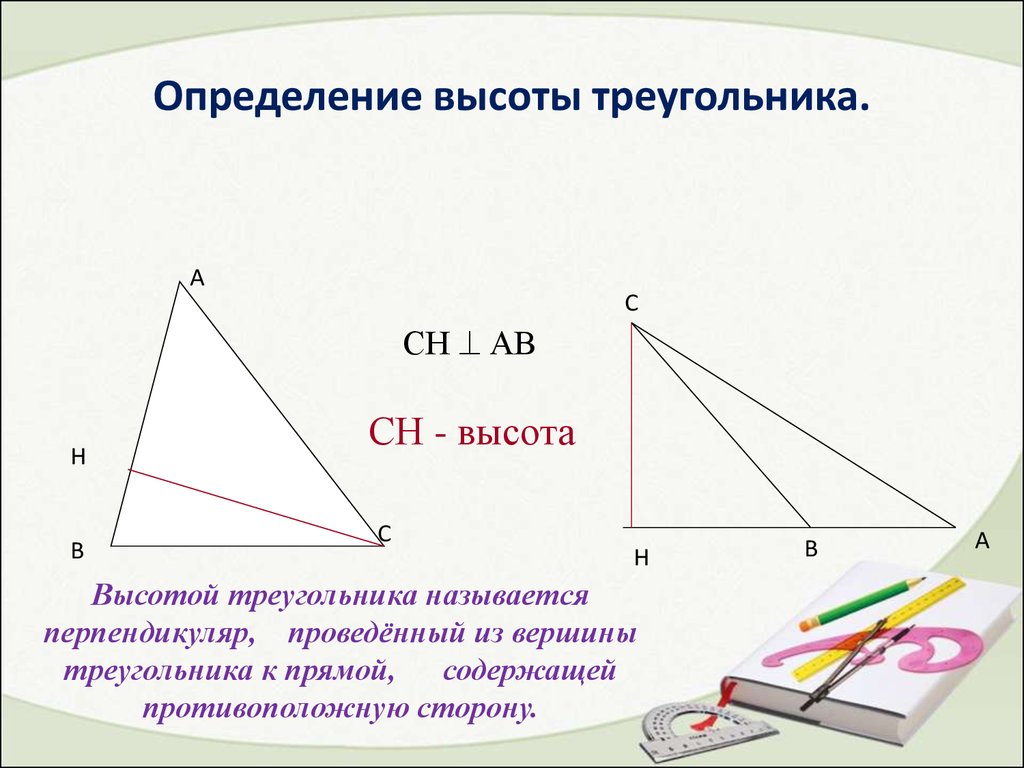
Высоту треугольника можно найти, если известна его площадь и длина основания: высота = 2 * площадь / основание.

Роскошный ремонт квартиры в центре Москвы // РУМ ТУР // Дизайн в стиле Классика и Ар Деко

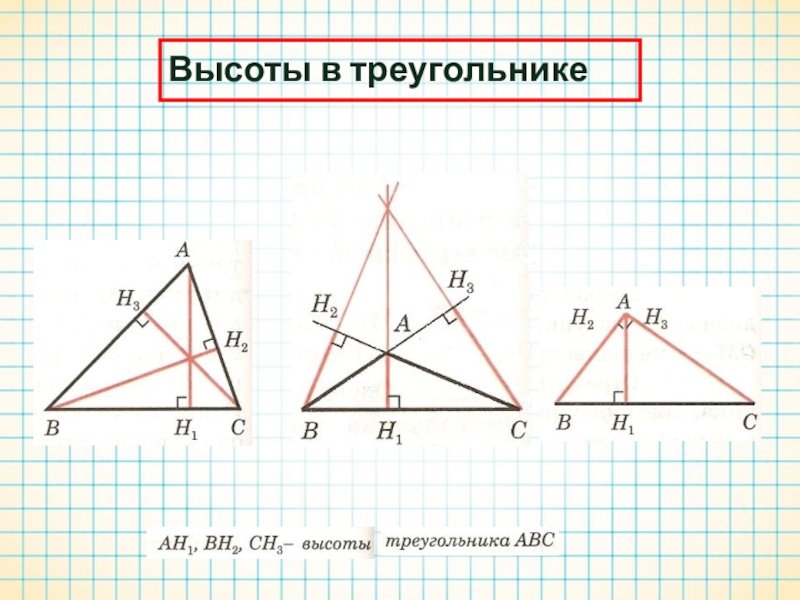
Не забывайте, что высота всегда перпендикулярна основанию треугольника, даже если основание находится на продолжении стороны.
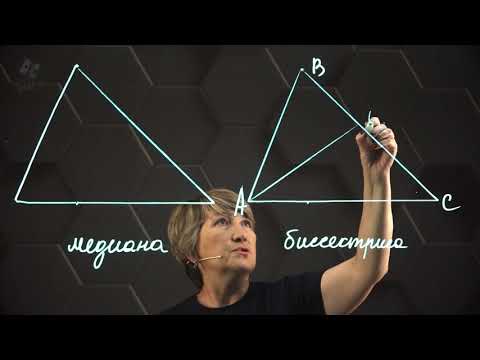
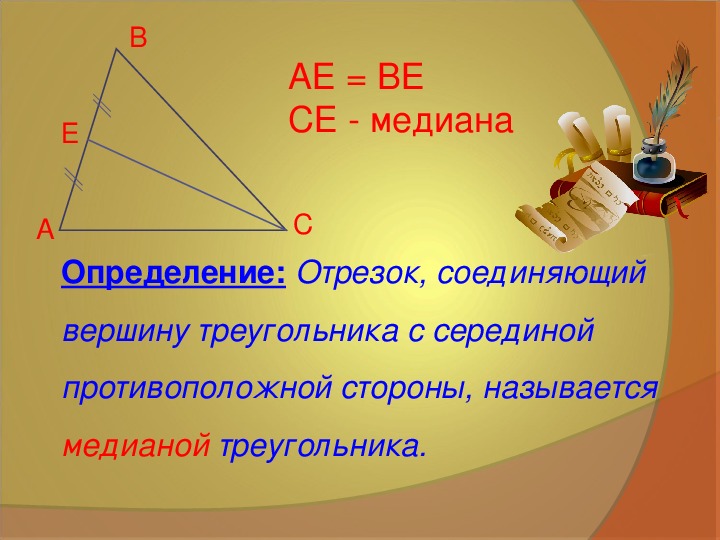
Высота, биссектриса, медиана. 7 класс.
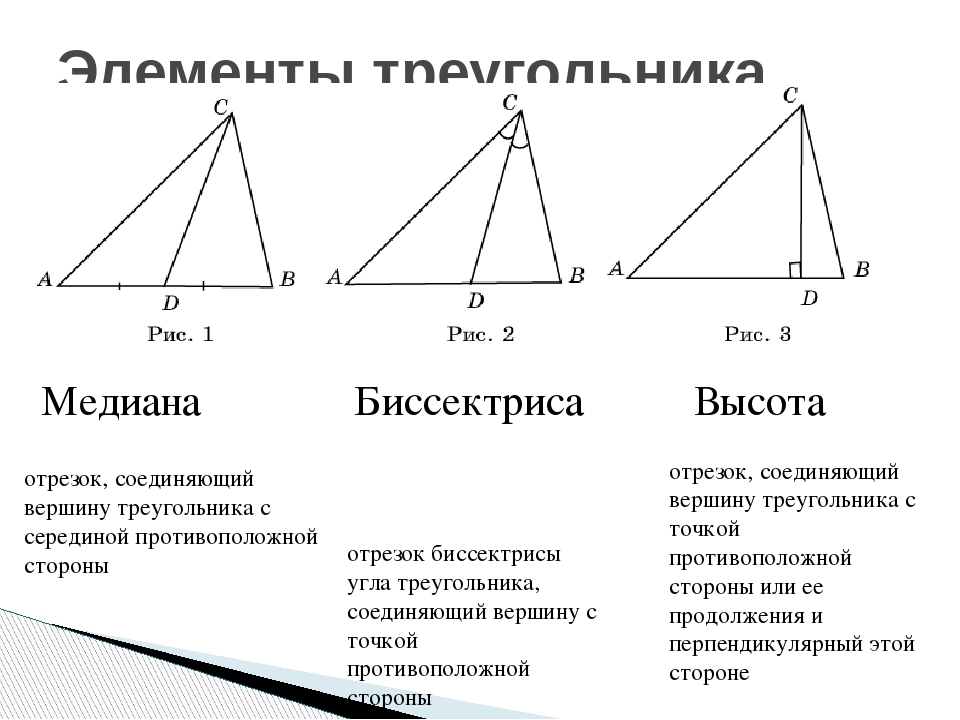
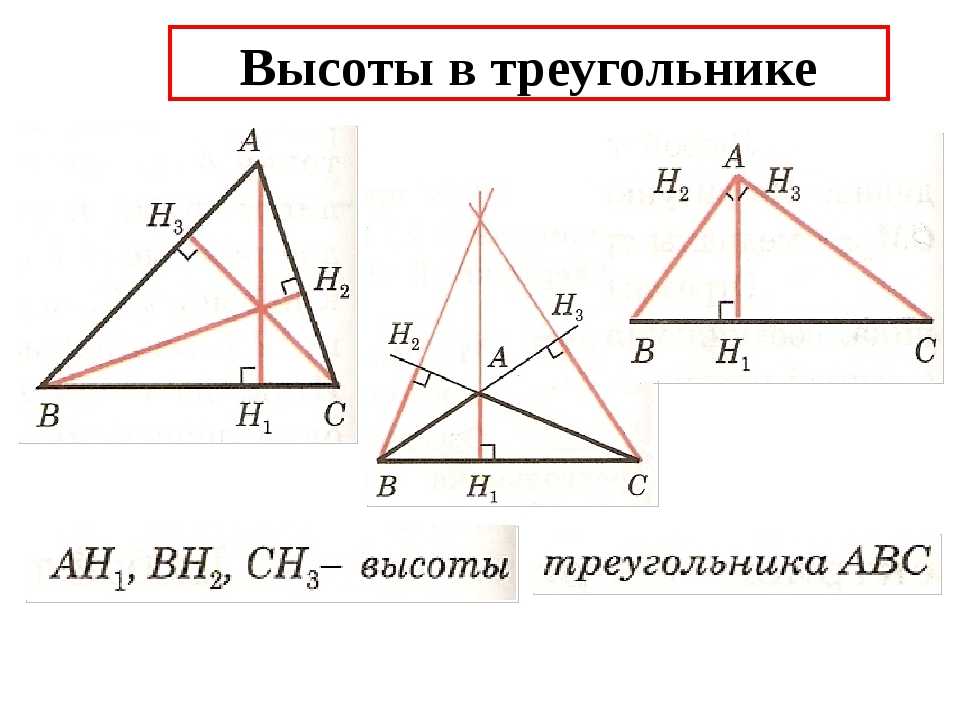
Для остроугольного треугольника высота всегда будет находиться внутри фигуры, в то время как для тупоугольного — снаружи.

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.
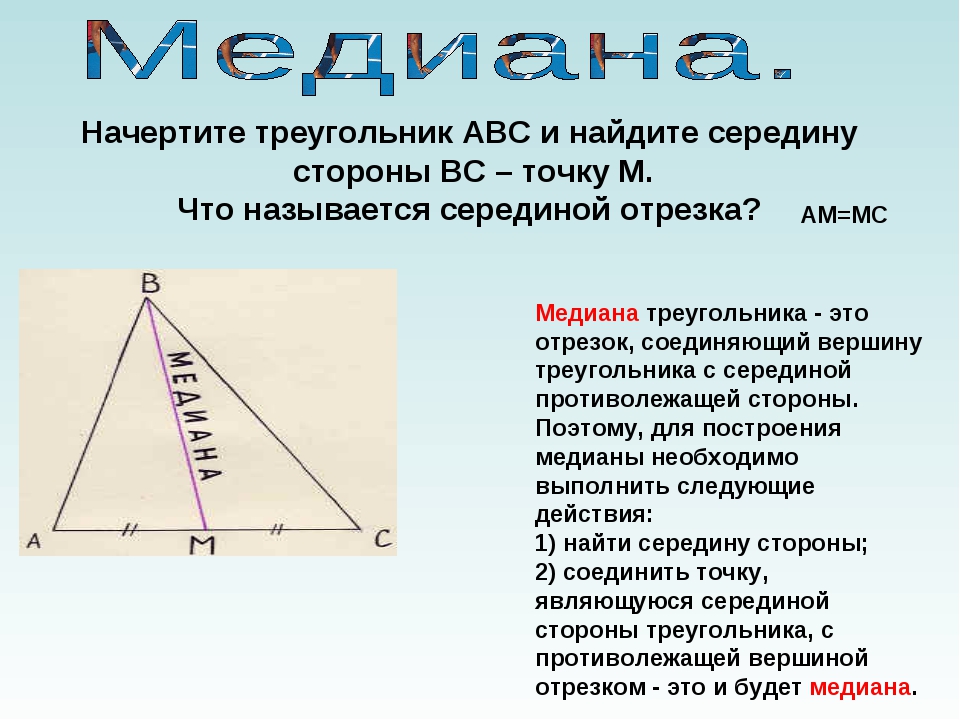
Используйте формулу площади для вычисления высоты, если другие параметры треугольника известны.
Признаки равенства треугольников. 7 класс.
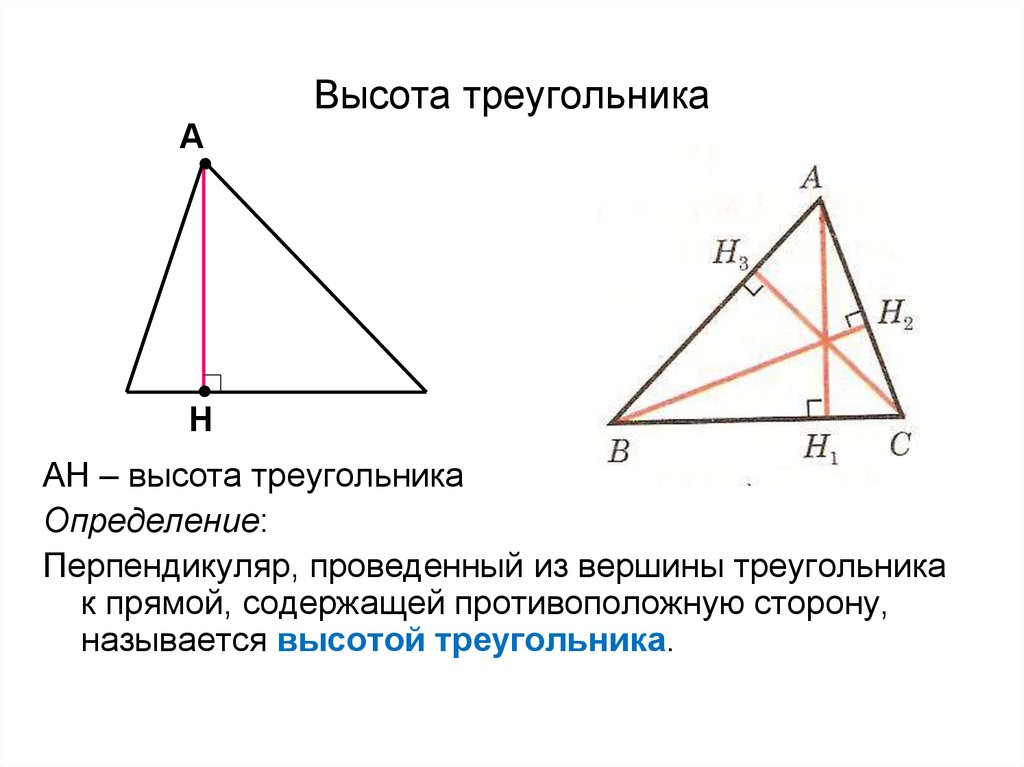
Для прямоугольного треугольника одной из сторон можно считать гипотенузу, а высоту — расстояние от прямого угла до гипотенузы.

Треугольники. 7 класс.
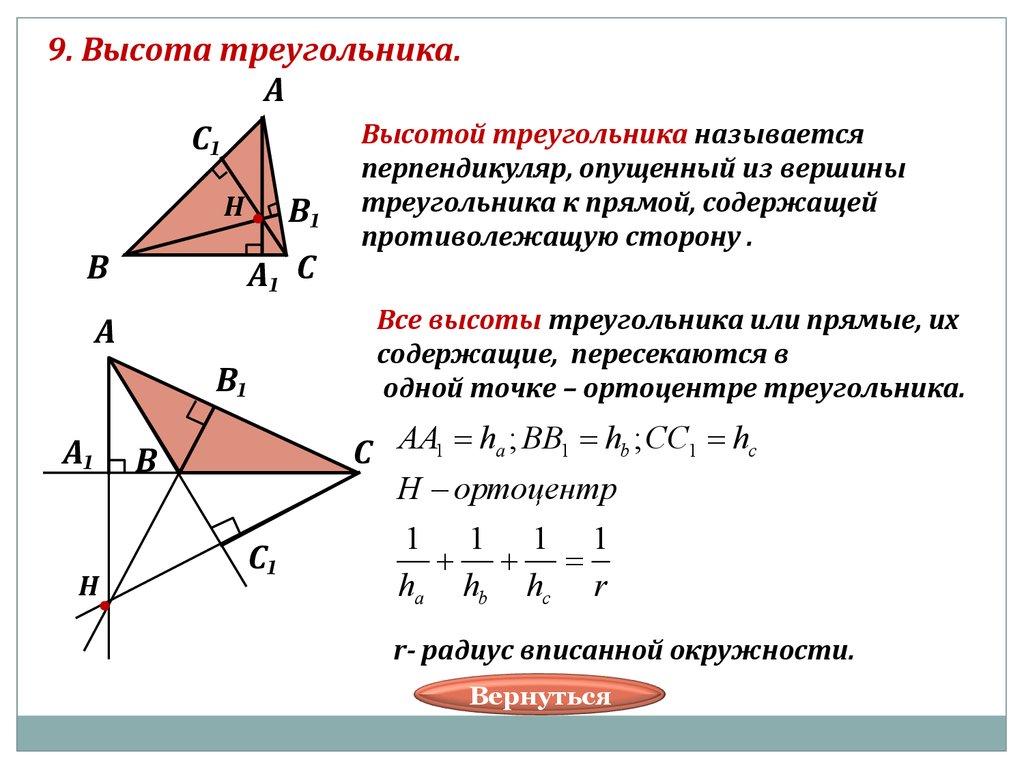
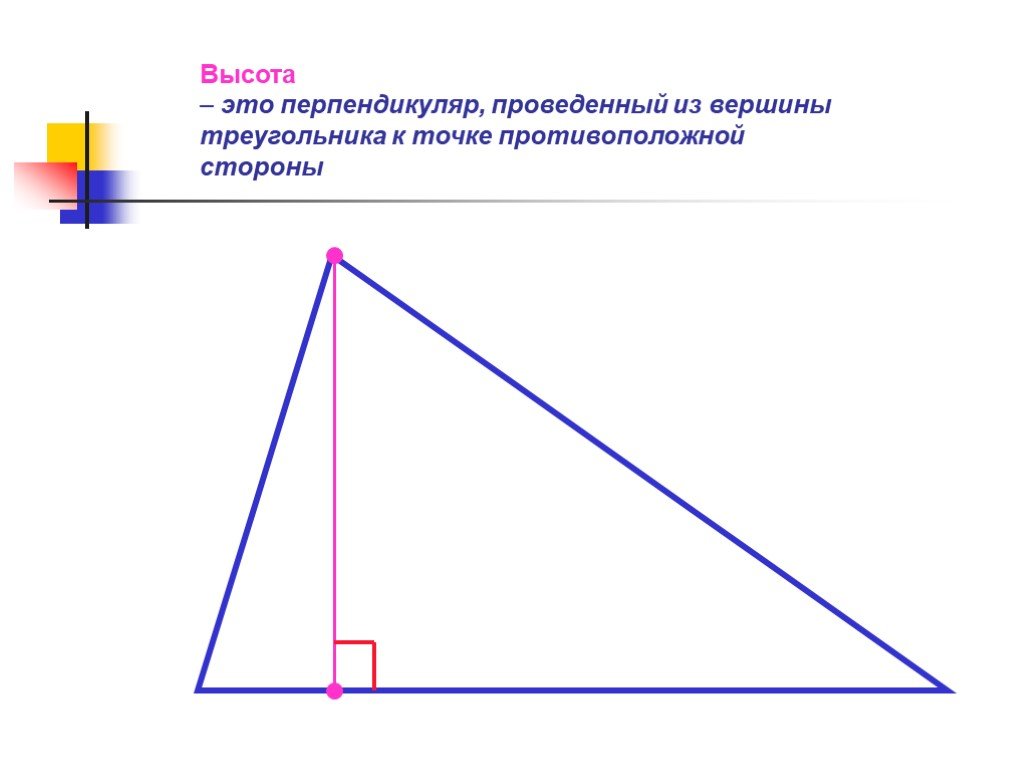
Если треугольник равнобедренный, высота будет не только перпендикуляром, но и медианой и биссектрисой.
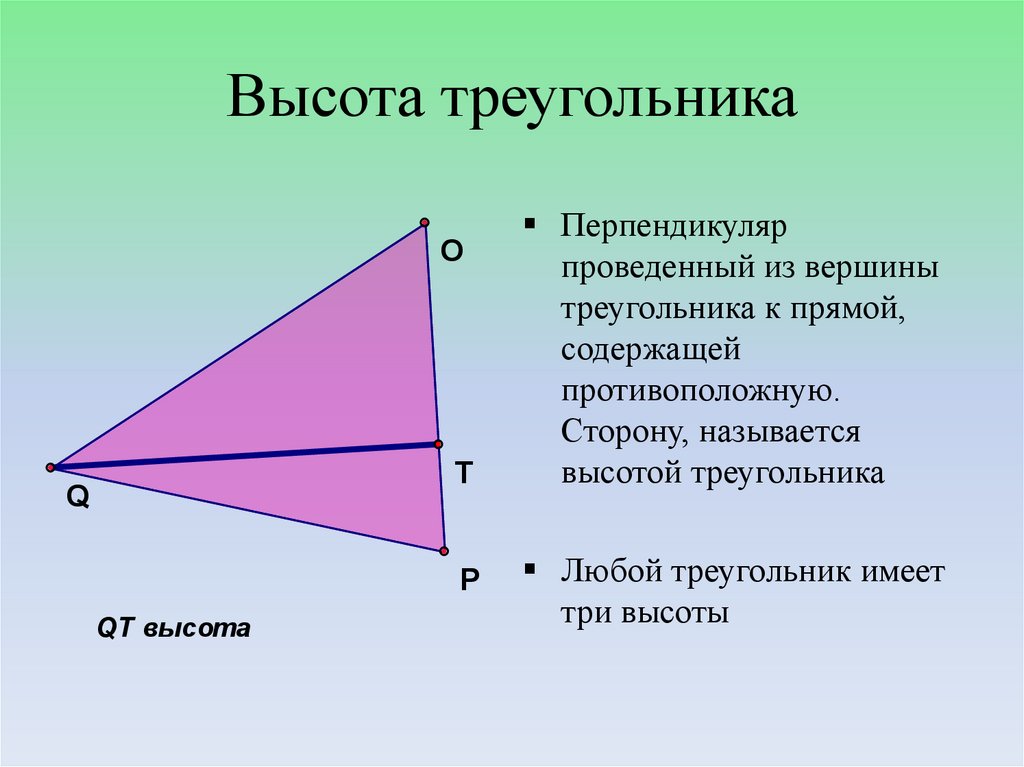

Когда вычисляете высоту, всегда учитывайте, что это перпендикулярное расстояние, и оно измеряется перпендикулярно основанию.

Самый короткий тест на интеллект Задача Массачусетского профессора
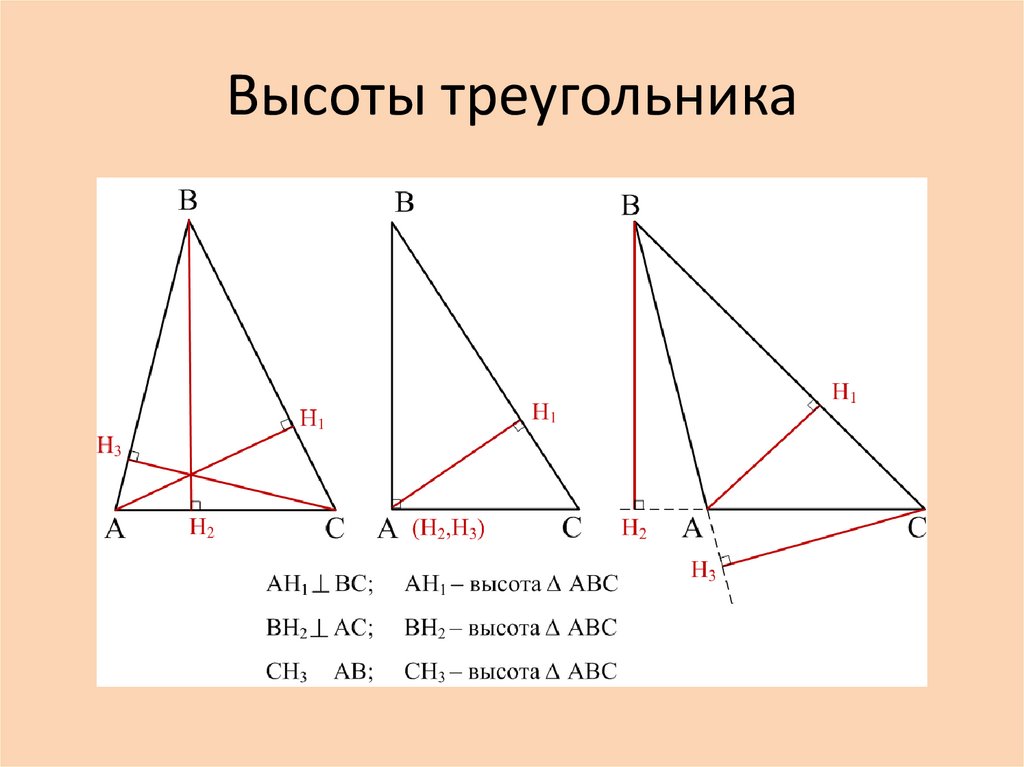

На практике для нахождения высоты можно использовать и теорему Пифагора, если у вас есть другие данные о треугольнике.
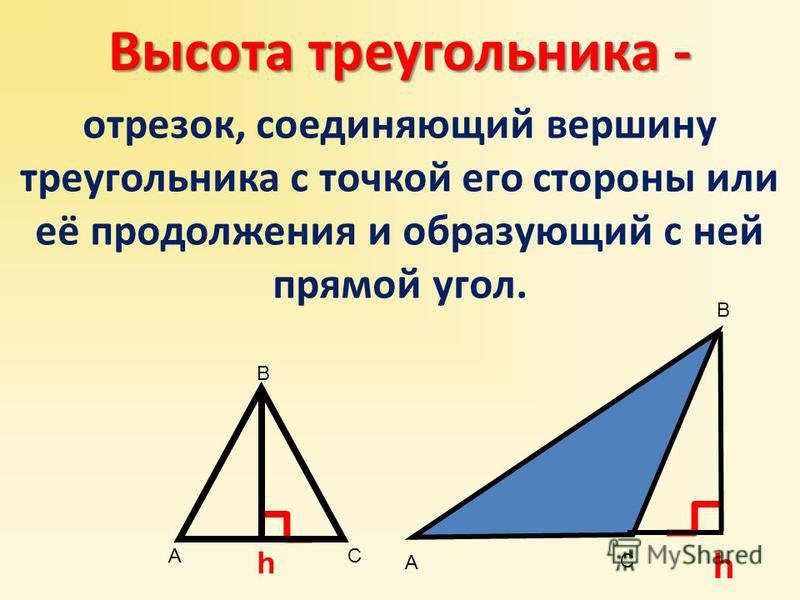
Для равностороннего треугольника высоту можно найти, используя формулу: высота = (a * √3) / 2, где a — длина стороны.
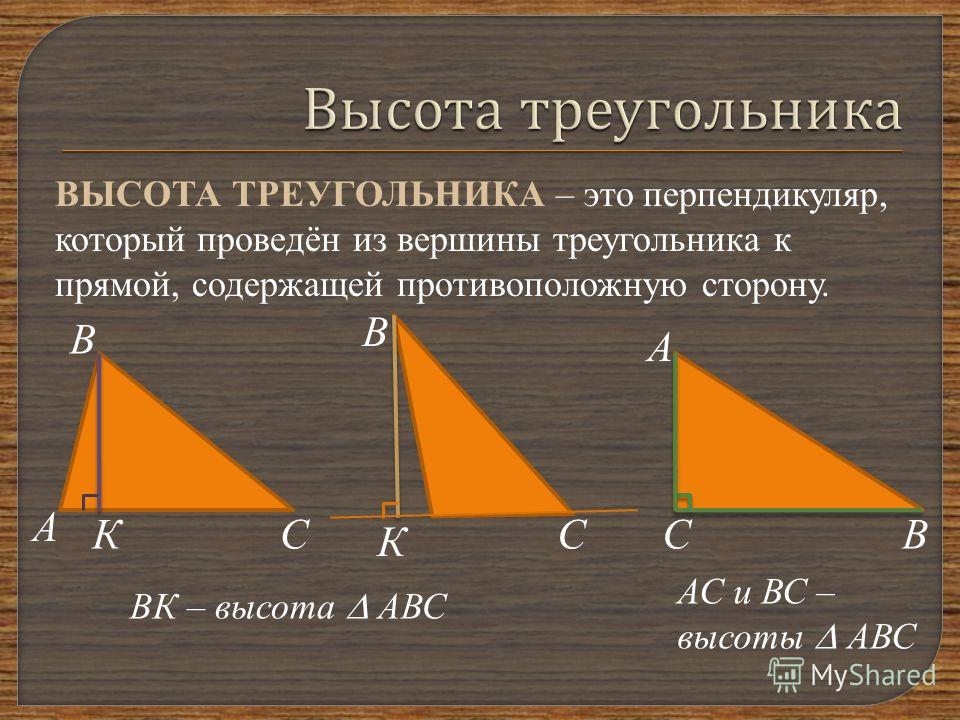
Понимание высоты важно не только для вычислений, но и для анализа свойств треугольников в геометрии, например, при решении задач на нахождение площади.
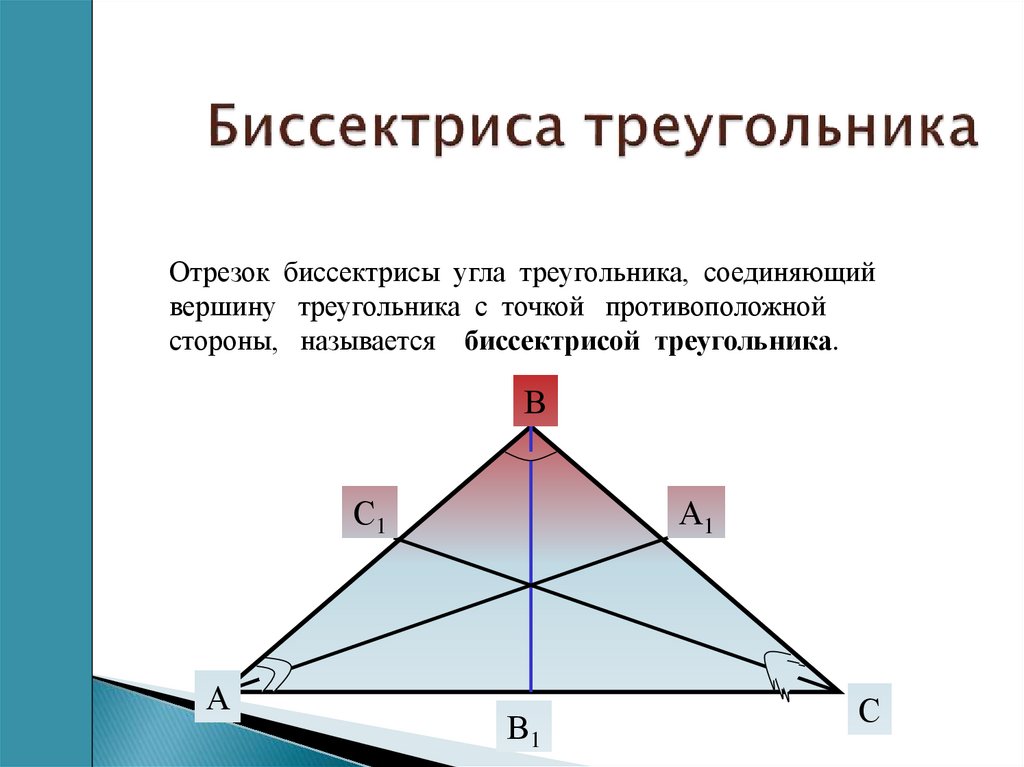

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника