Как правильно строить доказательство теорем в геометрии: советы и рекомендации
Доказательство теоремы в геометрии — это логическая последовательность, которая позволяет убедиться в истинности утверждения, опираясь на уже известные аксиомы, теоремы и свойства фигур. Важно научиться правильно выстраивать доказательства, используя различные методы, такие как метод математической индукции, контрапозиции или прямое доказательство. Этот процесс является не только основой математики, но и помогает развить аналитическое мышление.



Перед началом доказательства всегда четко сформулируйте условие задачи и теорему, которую нужно доказать.

Общие принципы доказательства в геометрии

Изучите все известные теоремы и свойства, которые могут быть использованы в процессе доказательства.

Геометрия. 7 класс. Теоремы. Т4. Перпендикуляр к прямой.

Стройте доказательство логично и последовательно, каждый шаг должен быть обоснован.

Edu: Сколькими способами можно доказать теорему Пифагора?
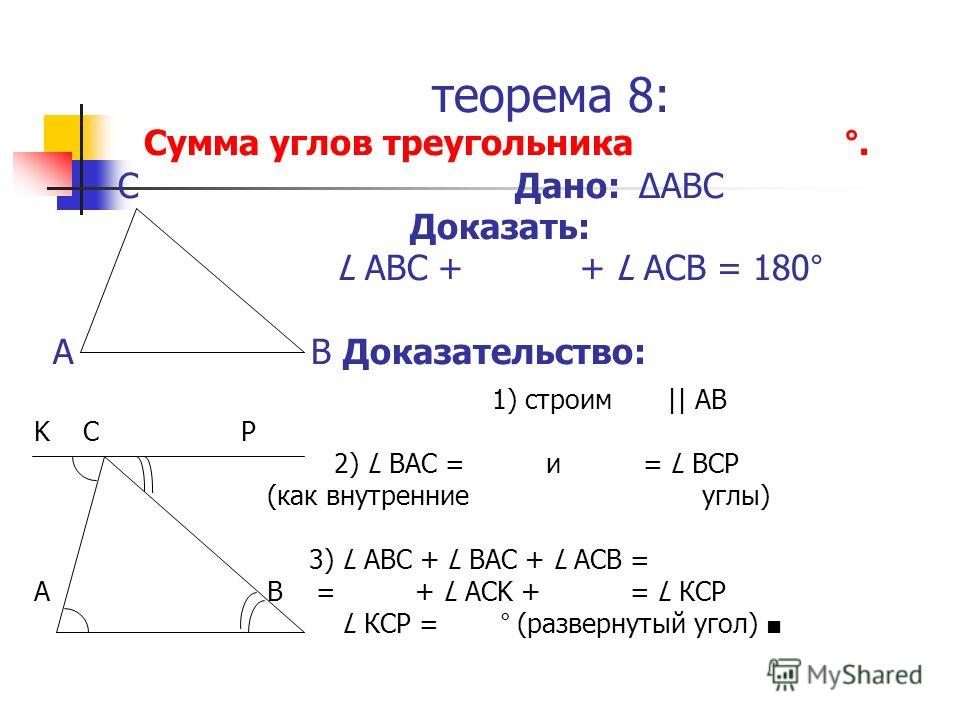
Используйте рисунки, чтобы визуализировать задачу и понять взаимосвязи между элементами геометрической фигуры.

Pythagorean theorem. Simple Proof

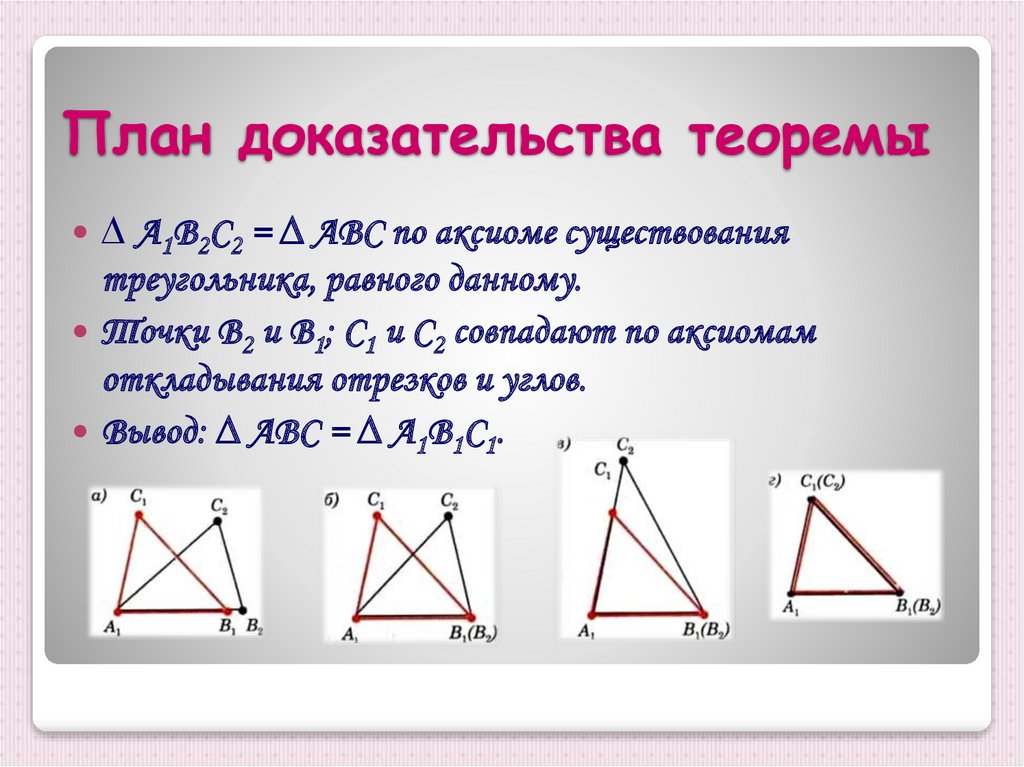
Не забывайте о математических аксиомах и определениях — они служат основой для большинства доказательств.
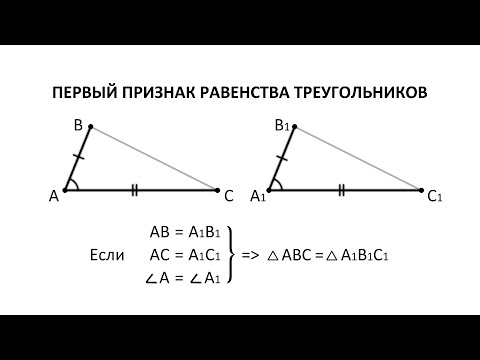
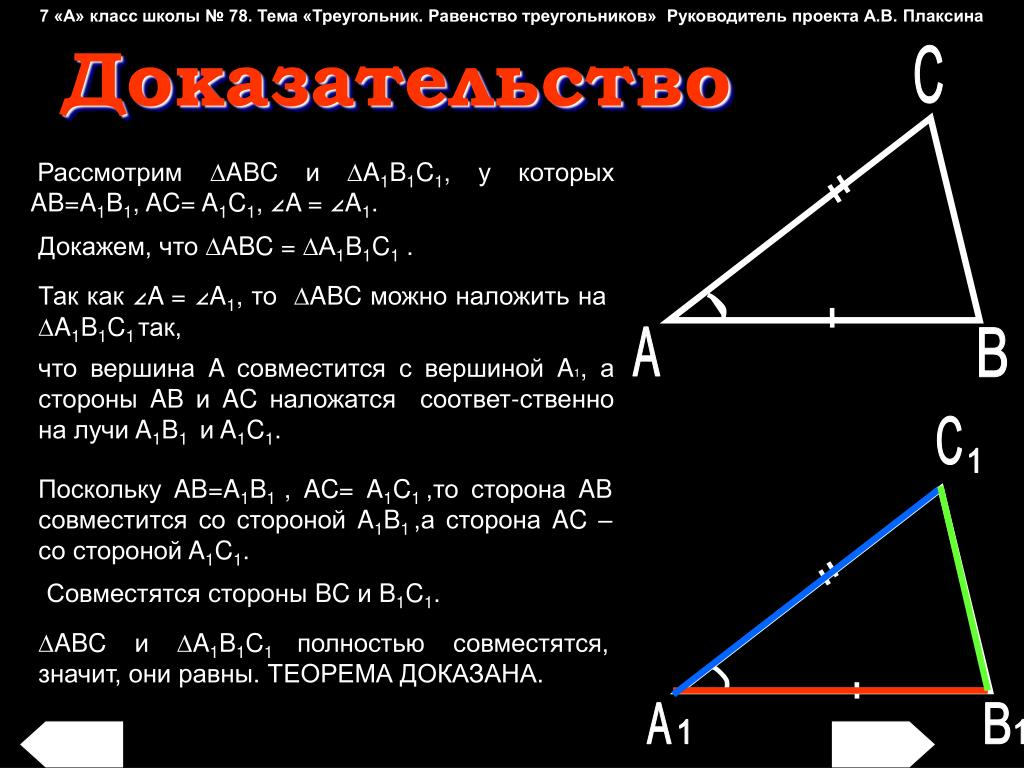
Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.

Если доказательство идет через противоречие, сформулируйте гипотезу и покажите, что ее ложность ведет к абсурду.
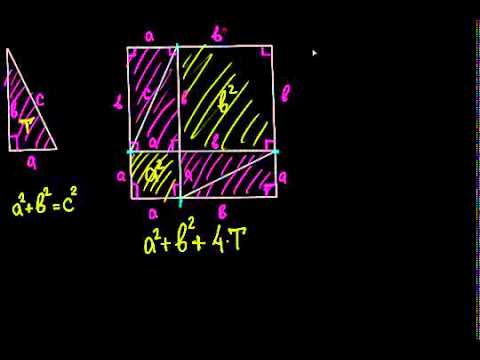
Геометрия: доказательство теоремы Пифагора
Метод индукции подходит для доказательства утверждений, которые справедливы для всех целых чисел или других объектов, образующих последовательность.

Теорема косинусов - Доказательство
Обычно лучше начинать с простых и очевидных случаев, чтобы затем развить более сложные шаги доказательства.

Признаки равенства треугольников - теорема пифагора - Математика - TutorOnline
Признаки равенства треугольников. 7 класс.

Иногда полезно разбить доказательство на несколько частей, каждая из которых будет отвечать за решение определенной подзадачи.

Первое доказательство. Геометрия 7 класс.

Постоянно проверяйте, не упустили ли вы важные детали или промежуточные шаги, которые могут быть критичными для доказательства.

