Роль алгебраического минора в теории матриц и его применения в расчетах
Алгебраический минор — это важная концепция в линейной алгебре, связанная с вычислением определителей и решением систем линейных уравнений. Этот инструмент используется при нахождении ранга матрицы, а также в более сложных задачах, например, при решении задач на нахождение собственных значений. Понимание алгебраического минора открывает широкие возможности для анализа линейных преобразований и структуры данных.



При решении задач с определителями всегда проверяйте размерность матрицы перед использованием алгебраического минора.

5 способов вычисления определителя ★ Какой способ лучше?


Для более эффективных вычислений с большими матрицами рассмотрите использование свойств минора, чтобы упростить задачу.

Линейная алгебра, 6 урок, Ранг матрицы

Помните, что алгебраический минор может быть полезен при нахождении обратной матрицы, особенно в вычислениях с матрицами порядка 3 и выше.
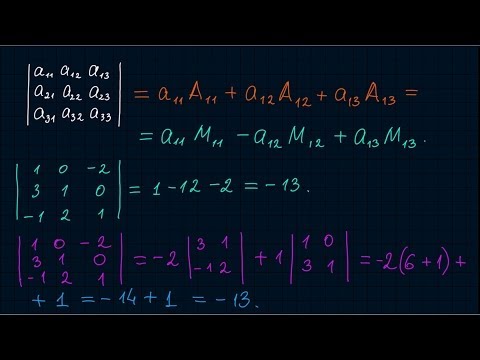
Миноры и алгебраические дополнения

Использование алгебраического минора помогает понять структуру линейных систем, что важно при решении задач на совместность уравнений.
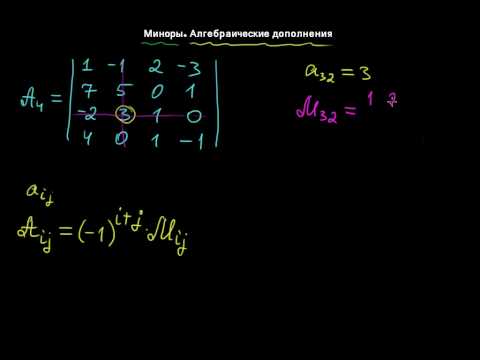
§12 Миноры. Алгебраические дополнения


Изучение алгебраических миноров поможет вам лучше понять свойства детерминантов и их роль в теории матриц.

Минор и алгебраическое дополнение матрицы как найти, решение примера

Для вычислений с минорами рекомендуется хорошо понимать принцип разложения по строкам и столбцам матрицы.
Файл со всеми формулами к ЕГЭ/ОГЭ в шапке #огэ #онлайншкола #математика #егэ
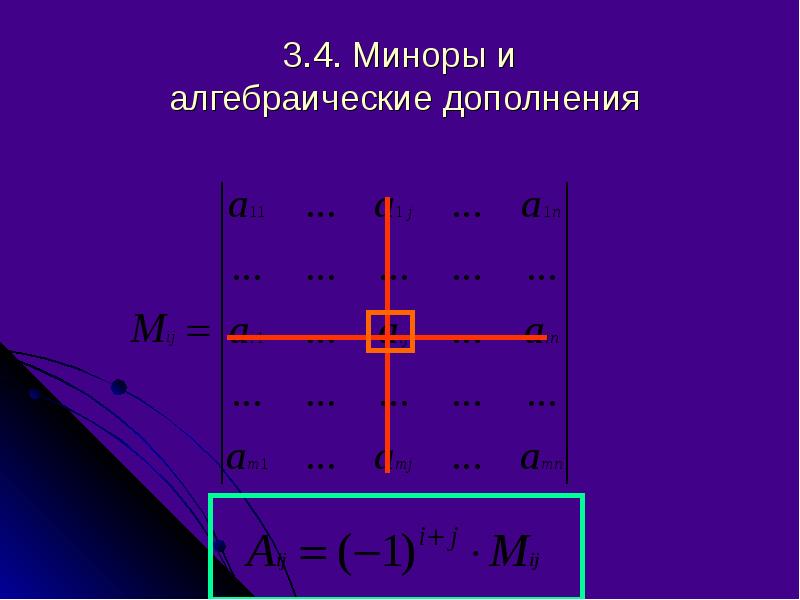

Алгебраические миноры широко применяются в вычислениях для поиска характеристических многочленов матриц.
При решении задач на нахождение собственных значений матрицы алгебраический минор может значительно ускорить процесс вычислений.

Как найти алгебраическое дополнение?

Урок 1. Матрицы, определитель матрицы и ранг матрицы - Высшая математика - TutorOnline
Для комплексных задач полезно изучать методы расширения теории минора, такие как разложение по элементам, для получения более точных результатов.

Алгебраический минор не только помогает решать задачи на определители, но и служит важным инструментом в более сложных разделах математики, таких как теория линейных операторов.

